3. Моделювання протилежних подій

Хай потрібно розіграти випробування, а кожному з яких подія з’являється з відомою ймовірністю і, відповідно, не з’являється з імовірністю .

Введемо до розгляду дискретну випадкову величину з двома можливими значеннями (для визначеності приймемо , ) і відповідними їм ймовірностями , . Домовимося вважати, що якщо у випробуванні величина набула можливе значення , то подія настала; якщо , то подія не настала, тобто з’явилась протилежна подія .

Таким чином, розігрування протилежних подій і зведено до розігрування дискретної випадкової величини із заданим законом розподілу:

	1	0

Для розігрування треба інтервал (0, 1) розбити точкою на два часткових інтервали: і . Потім вибирають випадкове число . Якщо потрапляє в інтервал , то (настала подія ); якщо потрапляє в інтервал , то (подія не настала).

Правило. Для того щоб розіграти випробування, в кожному з яких ймовірність появи події дорівнює і, отже, ймовірність настання протилежної події дорівнює , треба вибрати (наприклад, з таблиці випадкових чисел) випадкове число . Якщо , то подія настала, якщо , то з’явилася протилежна подія .

4. Моделювання повної групи подій

Розігрування повної групи несумісних подій , , …, ймовірності яких , , …, відомі, можна звести до розігрування дискретної випадкової величини з наступним законом розподілу (для визначеності приймемо , , …, ):

	1	2

Дійсно, достатньо вважати, що якщо у випробуванні величина набула значення , то настала подія . Справедливість цього твердження випливає з того, що число можливих значень дорівнює числу подій повної групи та ймовірності можливих значень і відповідних їм подій однакові: . Таким чином, поява у випробуванні події рівносильна події, що полягає в тому, що дискретна випадкова величина прийняла можливого значення .

Правило. Для того щоб розіграти випробування, в кожному з яких наступає одна з подій , , …, повної групи, ймовірності яких , , …, відомі, достатньо розіграти дискретну випадкову величину з наступним законом розподілу:

	1	2

Якщо у випробуванні величина набула можливе значення , то настала подія .

5. Моделювання неперервної випадкової величини. Метод обернених функцій

Нехай потрібно розіграти неперервну випадкову величину , тобто отримати послідовність її можливих значень , знаючи функцію розподілу .

Теорема. Якщо – випадкове число, то можливе значення неперервної випадкової величини , що розігрується, із заданою функцією розподілу , яке відповідає є коренем рівняння

.

Правило 1. Для того, щоб знайти можливе значення неперервної випадкової величини , знаючи її функцію розподілу , треба вибрати випадкове число , прирівняти його до функції розподілу і розв’язати відносно одержане рівняння

.

Зауваження 1. Якщо розв’язати це рівняння в явному вигляді не можна, то застосовують графічні або числові методи.

Зауваження 2. Відомо, що

.

Зокрема,

.

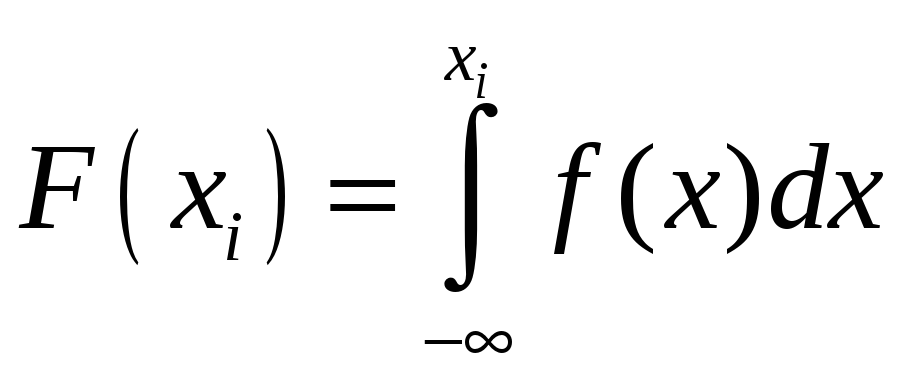Звідси випливає, що якщо відома щільність ймовірності , то для розігрування можна замість рівнянь розв’язати відносно рівняння

.

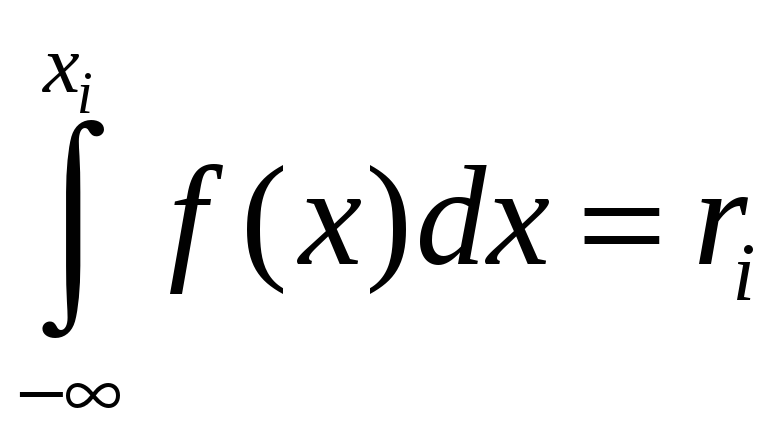Правило 2. Для того, щоб знайти можливе значення неперервної випадкової величини , знаючи її щільність розподілу , треба вибрати випадкове число і розв’язати відносно одержане рівняння

,

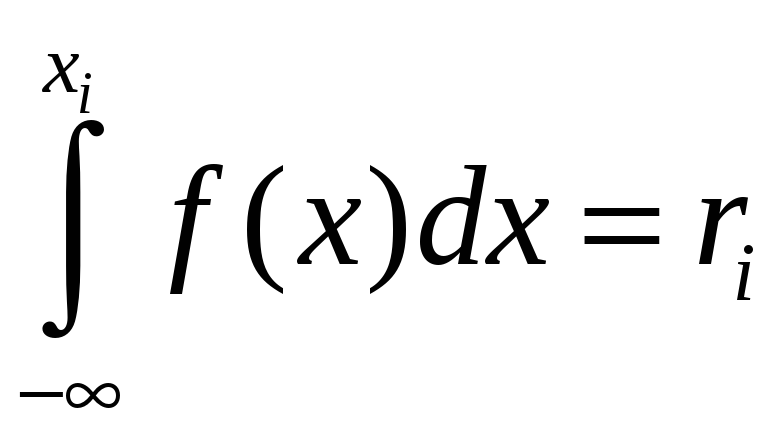або рівняння

,

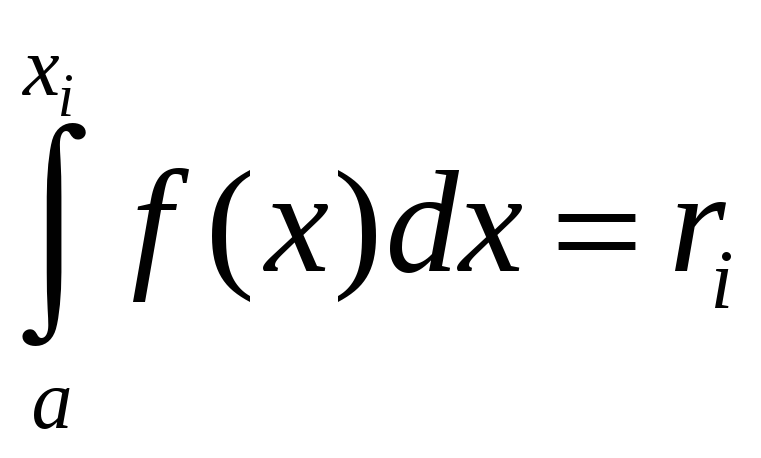де – найменше скінчене можливе значення .