ЛЕКЦІЯ 9. МОДЕЛЮВАННЯ ВИПАДКОВИХ ВЕЛИЧИН

МЕТОДОМ МОНТЕ-КАРЛО

1. Моделювання випадкових величин методом Монте-Карло. Основи методу Монте-Карло.

2. Моделювання дискретної випадкової величини.

3. Моделювання протилежних подій.

4. Моделювання повної групи подій.

5. Моделювання неперервної випадкової величини.

Література

1. Гмурман В.Е. Теория вероятностей и математическая статистика – М.: Высшая школа, 2002. – С. 363-379.

1. МОДЕЛЮВАННЯ ВИПАДКОВИХ ВЕЛИЧИН МЕТОДОМ

МОНТЕ-КАРЛО. ОСНОВИ МЕТОДУ МОНТЕ-КАРЛО

Датою народження методу Монте-Карло вважається 1949 р., коли американські вчені Н. Метрополіс і С. Улам опублікували статтю «Метод Монте-Карло», в якій систематично його виклали. Назва методу пов’язана з назвою міста Монте-Карло, де в гральних закладах (казино) грають у рулетку – одне з найпростіших пристроїв для отримання випадкових чисел, на використанні яких заснований цей метод.

ЕОМ дозволяють легко отримувати так звані псевдовипадкові числа (при розв’язуванні задач їх застосовують замість випадкових чисел); це призвело до широкого впровадження методу в різні галузі науки і техніки (статистична фізика, теорія масового обслуговування, теорія ігор та ін.). Метод Монте-Карло використовують для обчислення інтегралів, особливо багатовимірних, для розв’язування систем алгебраїчних рівнянь високого порядку, для дослідження різного роду складних систем (автоматичного управління, економічних, біологічних і т. д.).

Суть методу Монте-Карло полягає в наступному: потрібно знайти значення деякої величини, що вивчається. Для цього вибирають таку випадкову величину , математичне сподівання якої одно :

.

Практично ж роблять так: проводять випробувань, в результаті яких отримують можливих значень ; обчислюють їх середнє арифметичне

і вважають оцінкою (наближеним значенням) шуканого числа :

Оскільки метод Монте-Карло вимагає проведення великої кількості випробувань, його часто називають методом стохастичних випробувань. Теорія цього методу вказує, як найбільш доцільно вибрати випадкову величину , як знайти її можливі значення. Зокрема, розробляються способи зменшення дисперсії випадкових величин, що використовуються, в результаті чого зменшується помилка, яка допускається при заміні шуканого математичного сподівання його оцінкою .

Відшукання можливих значень випадкової величини (моделювання) називають «розігруванням випадкової величини». Викладемо лише деякі способи розігрування випадкових величин і зазначимо, як оцінити помилку, що припускається при цьому .

Оцінка похибки методу Монте-Карло

Нехай для одержання оцінки математичного очікування випадкової величини було проведено незалежних випробувань (розіграно можливих значень ) і по них була знайдена вибіркова середня , яка прийнята в якості шуканої оцінки: ). Зрозуміло, що якщо повторити дослід, то будуть отримані інші можливі значення , отже, інша середня, і інша оцінка . Вже звідси випливає, що отримати точну оцінку математичного сподівання неможливо. Природно, виникає питання про величину допустимої похибки. Обмежимося знаходженням лише верхньої межі допустимої помилки із заданою ймовірністю (надійністю) :

Верхня межа помилки , що нас цікавить, є не що інше, як «точність оцінки» математичного сподівання щодо вибіркової середньої за допомогою довірчих інтервалів. Тому скористаємося результатами, отриманими раніше, і розглянемо наступні три випадки.

1. Випадкова величина розподілена нормально і її середнє квадратичне відхилення відоме. У цьому випадку з надійністю верхня межа помилки

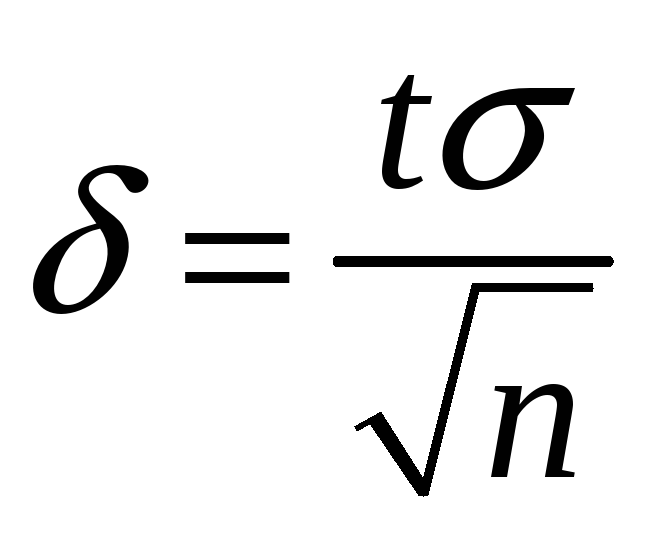, (1)

де – число випробувань (розіграних значень ); – значення аргументу функції Лапласа, при якому , – відоме середнє квадратичне відхилення .

2. Випадкова величина розподілена нормально, причому її середнє квадратичне відхилення невідоме. У цьому випадку з надійністю верхня межа помилки

, (2)

де – число випробувань; – «виправлене» середнє квадратичне відхилення, знаходять за таблицею значень .

Випадкова величина розподілена за законом, відмінним від нормального. У цьому випадку при досить великому числі випробувань () з надійністю, наближено рівною , верхня межа помилки може бути обчислена за формулою (1), якщо середнє квадратичне відхилення випадкової величини відоме, коли ж невідоме, то можна підставити у формулу (1) його оцінку -«виправлене» середнє квадратичне відхилення або скористатися формулою (2). Зауважимо, що чим більше , тим менша різниця між результатами, які дають обидві формули. Це пояснюється тим, що при розподіл Ст’юдента прямує до нормального.

Випадкові числа

Раніше було зазначено, що метод Монте-Карло заснований на застосуванні випадкових чисел; дамо означення цих чисел. Позначимо через неперервну випадкову величину, розподілену рівномірно в інтервалі (0, 1).

Випадковими числами називають можливі значення неперервної випадкової величини , розподіленої рівномірно в інтервалі (0, 1).

Насправді користуються не рівномірно розподіленою випадковою величиною , можливі значення якої, взагалі кажучи, мають нескінченне число десяткових знаків, а квазірівномірною випадковою величиною , можливі значення якої мають скінчене число знаків. В результаті заміни на величина, що розігрується, має не точно, а наближено заданий розподіл.

2. Моделювання дискретної випадкової величини

Нехай потрібно розіграти дискретну випадкову величину , тобто отримати послідовність її можливих значень , знаючи закон розподілу :

Позначимо через неперервну випадкову величину, розподілену рівномірно в інтервалі (0, 1), а через – її можливі значення, тобто випадкові числа.

Розіб’ємо інтервал на осі точками з координатами , , , , на часткових інтервалів , , , :

довжина ,

довжина ,

…………..

довжина .

Бачимо, що довжина часткового інтервалу з індексом дорівнює ймовірності з тим же індексом:

довжина .

Правило. Для того щоб розіграти дискретну випадкову величину, задану законом розподілу

треба: 1) розбити інтервал (0,1) осі на часткових інтервалів: , , … ;

2) вибрати (наприклад, з таблиці випадкових чисел) випадкове число .

Якщо потрапило в частковий інтервал , то дискретна випадкова величина, що розігрується, набула можливе значення .

Приклад. Розіграти 8 значень дискретної випадкової величини , закон розподілу якої заданий у вигляді таблиці

	3	11	24
	0,25	0,16	0,59

Розв’язання. Розіб’ємо інтервал (0,1) осі точками з координатами 0,25; ; на 3 часткові інтервали , , .

2. Випишемо з таблиці випадкових чисел вісім випадкових чисел, наприклад: 0,10; 0,37; 0,08; 0,99; 0,12; 0,66; 0,31; 0,85.

Випадкове число належить до часткового інтервалу , тому дискретна випадкова величина, що розігрується, набула можливого значення . Випадкове число належить до часткового інтервалу , тому випадкова величина набула можливого значення . Аналогічно отримаємо інші можливі значення.

Отже, розіграні можливі значення такі: 3; 11; 3; 24, 3; 24. 11, 24.