Вариант 11-VII

Данные:

Схема:

Рис. 1.1

Заданные параметры:

К=0.7 Т=0.35 τ=0.004

К₁=5 Т₁=0.07

К₂=5 Т₂=0.018

К₃=5 Т₃=0.45

К₅=4.2 Т₄=0.15

Т₅=0.12

I. Анализ системы автоматического управления.

1) Передаточная функция по управляющему воздействию в разомкнутом состоянии:

Пусть:

, ,,.

Звенья системы W₅(р) и W₁(p) соединены параллельно, поэтому их эквивалент будем считать по формуле:

Т.к все остальные звенья соединены последовательно, то передаточную функцию в разомкнутом состоянии будем искать как произведение этих звеньев:

Подставив численные значения, получим:

.

2) Передаточная функция в замкнутом состоянии:

.

3) Характеристическое уравнение системы в разомкнутом состоянии.

Для того, чтобы определить характеристическое уравнение системы необходимо приравнять знаменатель передаточной функции в разомкнутом состоянии к нулю.

=0

Характеристическое уравнение системы в замкнутом состоянии.

=0

4) Проверка устойчивости линейной САУ по критерию Михайлова.

Критерий Михайлова относиться к частотным критериям, и позволяет оценить устойчивость замкнутой системы по виду годографа, которой находится из характеристического уравнения.

Критерий устойчивости Михайлова: для устойчивости системы необходимо и достаточно, чтобы вектор D(jω), описывающий своим концом кривую Михайлова при изменении частоты ω от -∞ до +∞ , начав свое движение с положительной действительной оси и вращаясь против часовой стрелки, последовательно проходил n квадрантов, нигде не обращаясь в нуль.

D(p)==0

Делаем замену p=jω, получаем

D(jω)=

Выделяем из данного уравнения вещественную и мнимую части:

P(ω)=

Q(ω)=

Вычисляем полученные выражения Q(ω) иP(ω) подставляя в них значения частотω. Полученные результаты занесены в таблицу 1.1.

Таблица 1.1 Критерий Михайлова.

ω, с-1	0	1	3	5	7	9	11
P(ω)	46	45.385	41.029	35.313	34.226	46.754	84.878
Q(ω)	0	5.193	13.346	14.801	5.091	-20.249	-65.684

Рис. 1.2 Критерий Михайлова.

Из графика видно, что кривая Михайлова проходит через три квадранта (I,IV,III) по часовой стрелке, это означает, что система не устойчива.

5) Проверка устойчивости линейной сау с помощью критерия Найквиста.

Критерий Найквиста – графический критерий, в котором вывод об устойчивости и не устойчивости системы делается на основании характеристик: ЛАЧХ и ЛФЧХ. Кроме устойчивости по этим характеристикам можно судить также и о запасе устойчивости данной системы.

Критерий устойчивости Найквиста в логарифмических координатах: если замкнутая система устойчива, то для устойчивости данной САУ необходимо и достаточно, чтобы ЛФЧХ при изменении частоты ω от 0 до ∞ пересекала линию 180⁰ справа от частоты среза ( точка пересечения ЛАЧХ с осью абсцисс .)

Преобразуем структурную схему в схему, состоящую из простых , элементарных передаточных звеньев. После преобразований, которые были сделаны выше, передаточная функция заданной САУ в разомкнутом состоянии содержит 4 последовательно соединенных звеньев.

Рис. 1.3

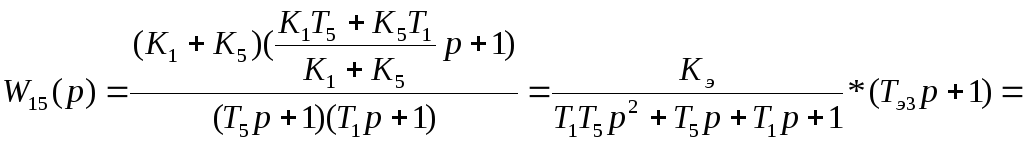
Где:

Kэ=K1+K5+5+4.2=9.2;

Tэ1=0.07*0.12=0.0084;

Tэ2=0.19;

Tэ3=3.39.

Первое звено необходимо разложить на три: два апериодических и форсирующее 1-го порядка. Найдем коэффициент демпфирования колебательного звена:

.

Из уравнения можно выразить следующее:

T²=0.0084

инерционное звено 2-го порядка необходимо разложить на 2 апериодических.

0.0084p²+0.19p+1=0

0.0084p²+0.19p+1=0.0084(p+9.52)(p+13.1)

После проделанного преобразования мы получили 3 апериодических звена, 1 форсирующее 1-го порядка, 1 звено запаздывания и 1 интегрирующее.

Рис. 1.4

Построим логарифмическую амплитудно-частотную характеристику (ЛАЧХ) в разомкнутом состоянии.

К_р=К₁*К₂*К₃*К₄=115*0.08*5*1=46

20lgК_р=33.26 (дБ)

Находим частоты сопряжения:

, (с^-1)lgω₁=lg10=1 (дек)

, (с^-1)lgω₂=lg12.5=1.09 (дек)

, (с^-1)lgω₃=lg0.295=-0.53 (дек)

, (с^-1)lgω₄=lg2.22=0.345 (дек)

В соответствии с количеством звеньев, которые влияют на ЛАЧХ , график имеет 5 участков (т.к звено запаздывания не влияет на ЛАЧХ)

Участок 1. Наклон -20 дБ/дек

Участок 2. Наклон -20дБ/дек +20дБ/дек =0дБ/дек

Участок 3. Наклон 0дБ/дек -20дБ/дек =-20дБ/дек

Участок 4. Наклон -20дБ/дек -20дБ/дек =-40дБ/дек

Участок 5. Наклон -40дБ/дек -20дБ/дек =-60дБ/дек

ЛАЧХ построена на рисунке 1.5

Теперь построим для заданной САУ логарифмическую фазо-частотную характеристику (ЛФЧХ), для этого по оси ординат откладывают угол φ, а по абсцисс lgω в декадах. Вид фазовой частной характеристики определяем по таблице 1.2

Таблица 1.2 Частотные характеристики звеньев.

Тип звена	Фазовая частотная характеристика
Апериодическое 1-го порядка
Интегрирующее звено	-900
Форсирующее 1-го порядка
Звено запаздывания

Запишем выражениядля каждого звена, входящего в заданную САУ.

Итоговое выражение фазы для всей системы выглядит следующим образом:

Подставив значения ω, получим следующие результаты:

Таблица 1.3 Фазочастотная характеристика.

ω, c-1	, град	lgω
0.295	-55.517	-0.53
2.22	-74.611	0.34
3	-88.594	0.47
4	-103.8	0.6
5	-116.6	0.69
6	-134.29	0.82
10	-160.56	1
12.5	-174.8	1.096
14	-181.728	1.146

График ЛФЧХ построен на рисунке 1.5