2. Частотные характеристики сау.

Пусть входное воздействие g(t) представляет собой гармоническую функцию вида

Использовав формулу Эйлера, можно записать

.

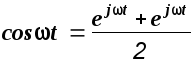Тогда входное воздействие можно представить в виде суммы двух воздействий

(1.30)

Дифференциальное уравнение системы в изображениях по Лапласу запишется в виде

(1.31)

где полином A(s) имеет порядок n, а полином B(s)-порядок m .

Пусть на вход системы подано воздействие вида g₁(t). Частное решение дифференциального уравнения будем искать в виде

Здесь W(j) - некоторая функция частоты .

Подставив g₁(t) и x₁(t) в (1.31), сократив полученное выражение на G_m/2 и e^-jt, получим

Отсюда

(1.32)

Сравнивая (1.32) и (1.29), можно заключить, что функция W(j) получается из передаточной функции W(s) простой заменой s=j. Эта замена с математической точки зрения означает переход от преобразования Лапласа к преобразованию Фурье [1,13] .

Функция W(j) называется частотной передаточной функцией системы. Комплексную функцию W(j) представим в виде

(1.33)

Тогда

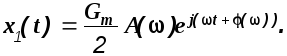
Если в (1.31) подставить функцию то после преобразований аналогичных предыдущим, получим

В соответствии с принципом суперпозиции

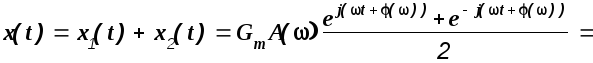
(1.34)

Это выражение показывает, что вынужденные колебания, вызываемые в устойчивой линейной динамической системе гармоническим входным воздействием, представляют собой гармоническую функцию времени, имеющую ту же частоту, что и входное воздействие, но отличающуюся от последнего по амплитуде и по фазе.

Зависимость отношения А() амплитуды выходного сигнала к амплитуде входного сигнала от частоты называется амплитудной частотной характеристикой (АЧХ) системы.

Зависимость фазового сдвига () между входным и выходным сигналами от частоты называется фазовой частотной характеристикой (ФЧХ) системы.

С этой точки зрения частотную передаточную функцию W(j) называют также амплитудно-фазовой частотной характеристикой (АФЧХ) системы.

Методика определения частотных характеристик системы следующая.

1).В передаточной функции системы делают замену s=j и полученную АФЧХ представляют в виде суммы вещественной и мнимой частей.

Функцию U() называют вещественной частотной характеристикой, а функцию V()- мнимой частотной характеристикой.

2). Определяют АЧХ и ФЧХ.

(1.35)

(1.36)

Пример. Определить частотные характеристики для звена с передаточной функцией

Делаем замену s=j.

Отсюда

V() = () A() ()

k 0 1/T 

U() 4

45⁰ -45⁰

A()

90⁰



Рис. 1.8. Частотные характеристики звена с передаточной функцией

Частотные характеристики широко используются при анализе и синтезе САУ и составляют основу рассматриваемой классической теории автоматического управления.