Теорема (достаточный признак разложимости функции в ряд Тейлора)

Пусть , причем все производные -ного порядка в в совокупности ограничены, т.е. . Тогда в функция разложима в свой ряд.

§3.4. Разложение в ряд Тейлора некоторых функций.

Все разложения будем рассматривать в точке (ряд Маклорена).

1. Рассмотрим функцию .

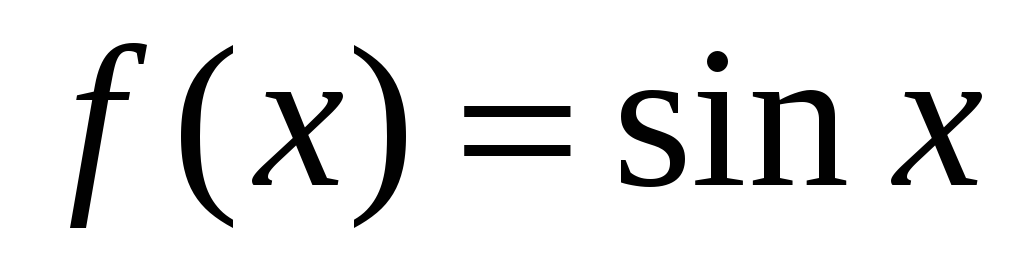Для этой функции имеем, что для и при любом действительном .

Вычислим коэффициенты ряда Тейлора:

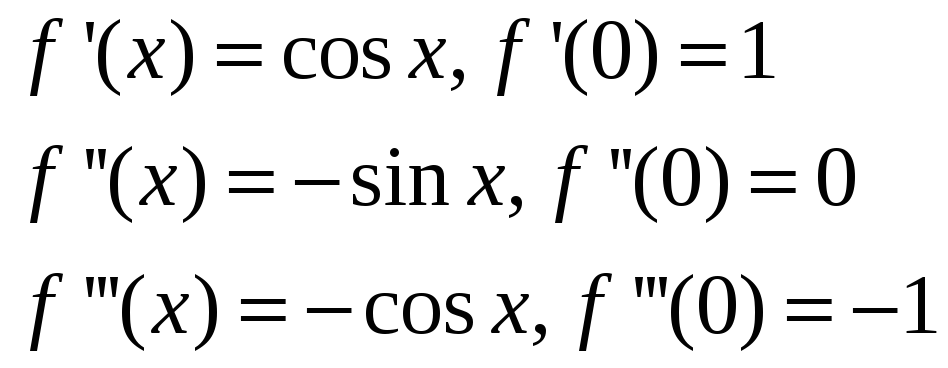
2. Рассмотрим функцию 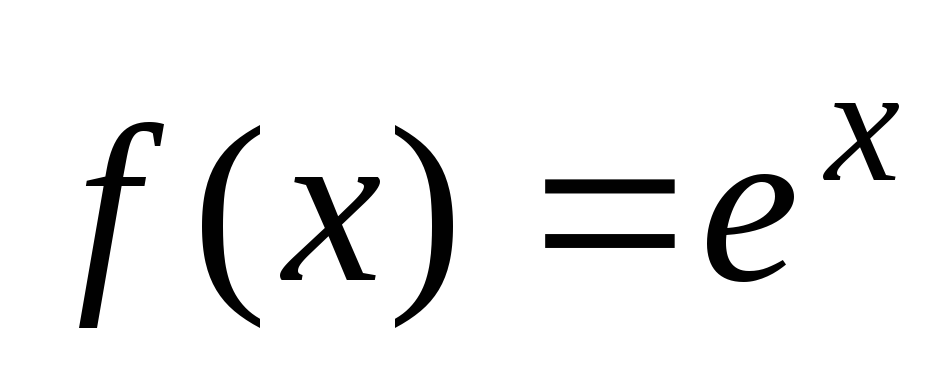. В любом промежутке вида 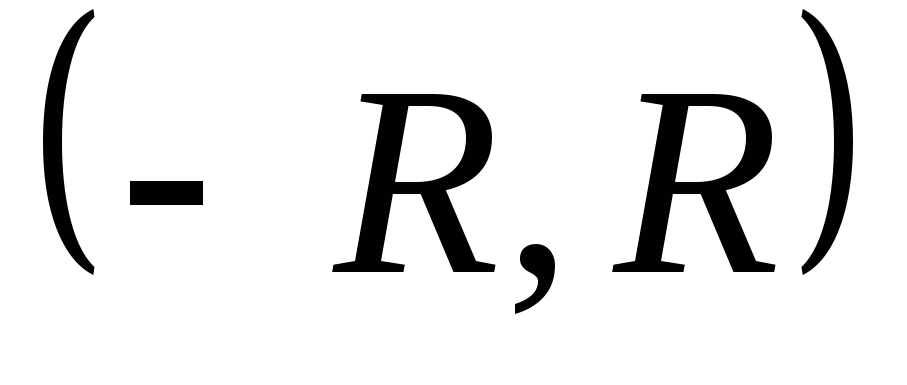выполняется:

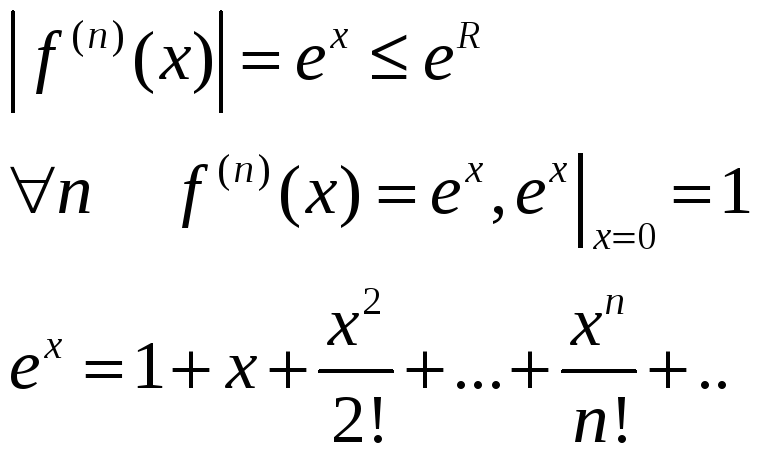
3. Логарифмическая функция.

Дифференцирую по и разлагая полученную производную по формуле геометрической прогрессии имеем:

при .

Интегрируя это равенство почленно, получаем:

Данное разложение в промежутке и оно так же верно при .

4.

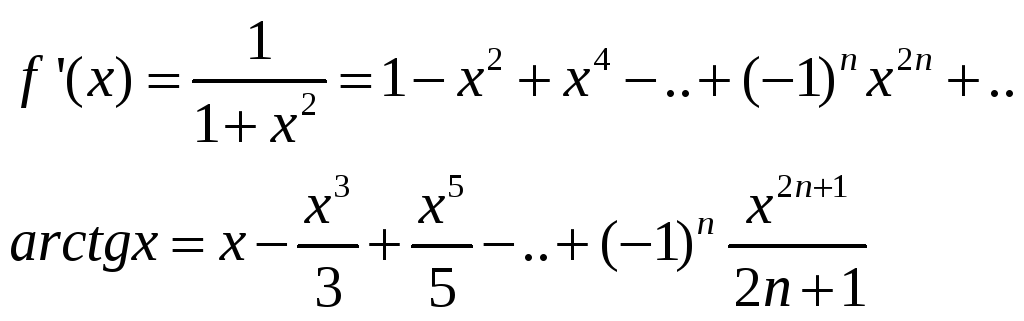
Данное разложение справедливо в промежутке ( в нем непрерывен, поэтому функция разложима).

4. Биноминальное разложение:

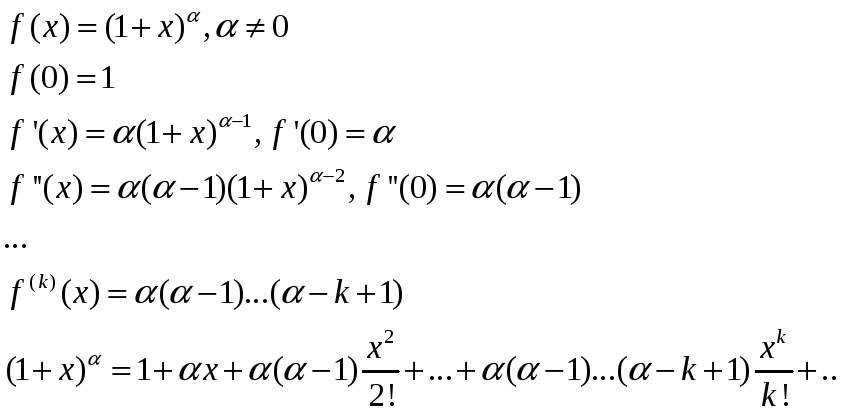
Применяя признак Даламбера, можно найти радиус сходимости:

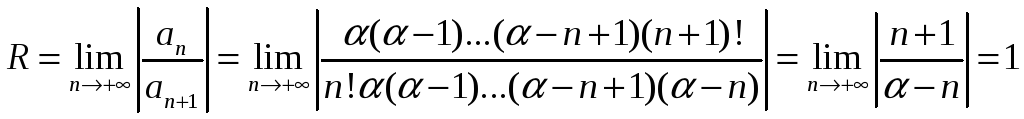- ряд сходится в интервале (-1,1).

§3.5. Некоторые применения степенных рядов.

. Степенные ряды могут применяться для приближенного вычисления функции. Например, зная разложение вычислим значение этой функции при с точностью .

Так как ряд знакочередующийся лейбницевского типа, то остаток по модулю не превосходит первого отброшенного члена.

Оценим погрешность после отбрасывания члена, т.е.

Остается подобрать такое , чтобы

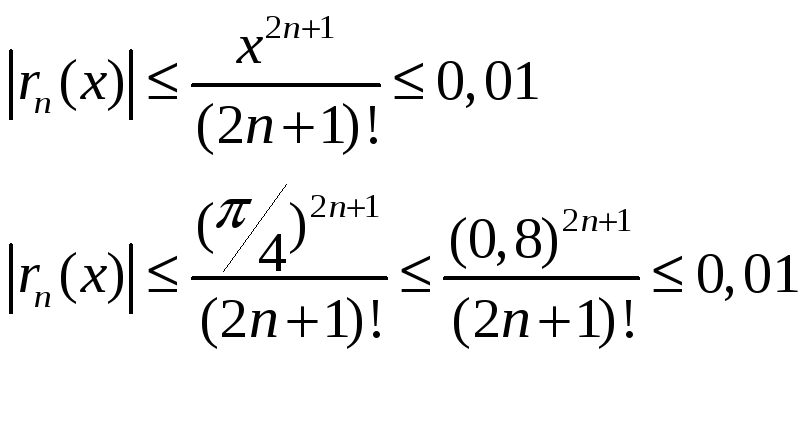уже при

с точностью 0,01 на промежутке

Разложение функции можно использовать для вычисления значений этих функции при любых значениях с любой степенью точности, т.к. эти разложения справедливы для всей числовой оси.

Ряд для логарифмов (1) для , хотя и знакопеременный, но сходится медленно, а при расходится. Чтобы ускорить сходимость ряда и сделать возможным вычисление логарифмов чисел из ряда (1) вычитают ряд (2)

(3)

Полагая в формуле (3) , получим (4)

С помощью ряда (4), сходящегося достаточно быстро, отправляясь от можно найти всех натуральных чисел.

Ряд для можно использовать для вычисления числа с любой точностью.

Полагая в разложении , получаем

В силу знакопеременности легко оценивается погрешность, допускаемая заменой его суммы частичной суммой.

Ряд можно использовать для извлечения корней.

Пример:

.Для вычисления интегралов, не берущихся в конечном виде.

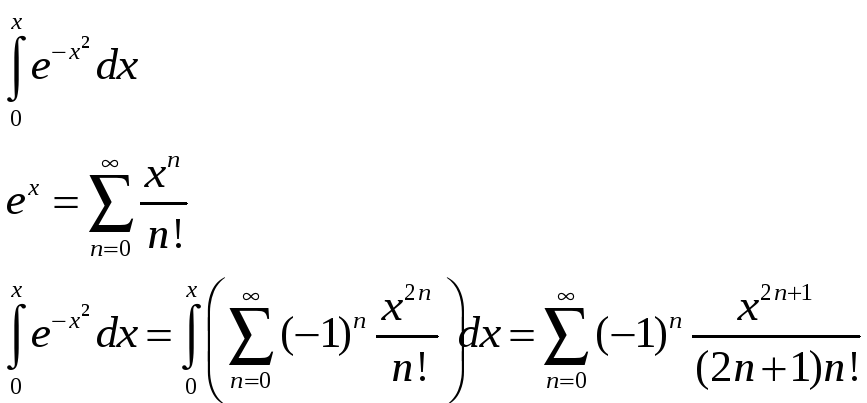
Так как ряд сходится на всей числовой оси, то его можно почленно интегрировать. Результат получаем в виде ряда, но это точный результат, первообразной же функции для этого ряда не существует.