§3.1. Степенные ряды.

. Это частный случай функциональных рядов, когда в качестве функций идут функции вида , где .

Степенным рядом называют функциональный ряд вида:

(1) или вида (2)

Заменой на новую переменную ряд (2) легко приводится к виду ряда (1), который соответствует .

Область сходимости степенного ряда всегда есть не пустое множество, т.к. очевидно, что для ряда (1) есть сходимость, по крайней мере, в точке , а для ряда (2) в точке .

. Промежуток и радиус сходимости степенного ряда.

Теорема 1.

Для произвольного степенного ряда вида (1) справедливо:

1) Область сходимости есть промежуток вида , где .

2) Число .

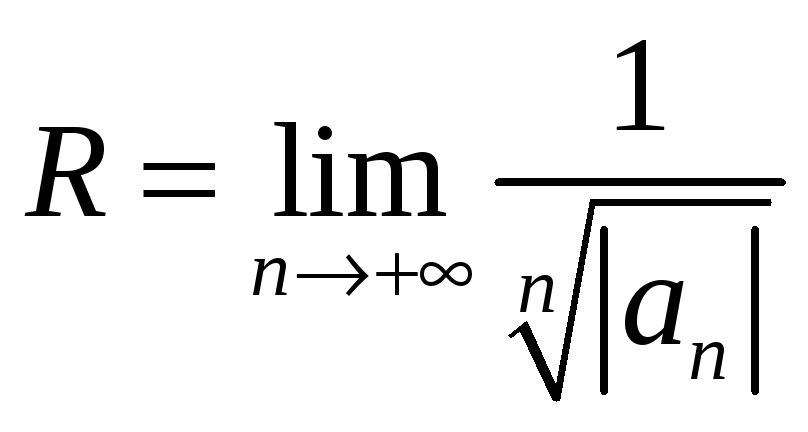3) Внутри промежутка степенной ряд сходится абсолютно.

Число называется радиусом сходимости степенного ряда, а область сходимости степенного ряда называют промежутком сходимости.

Замечание: согласно теореме область сходимости степенного ряда есть промежуток вида , так что, если известно, то для уточнения всей области сходимости необходимо выяснить сходимость в концевых точках .

Теорема 2 (другая формула для радиуса сходимости).

Если существует 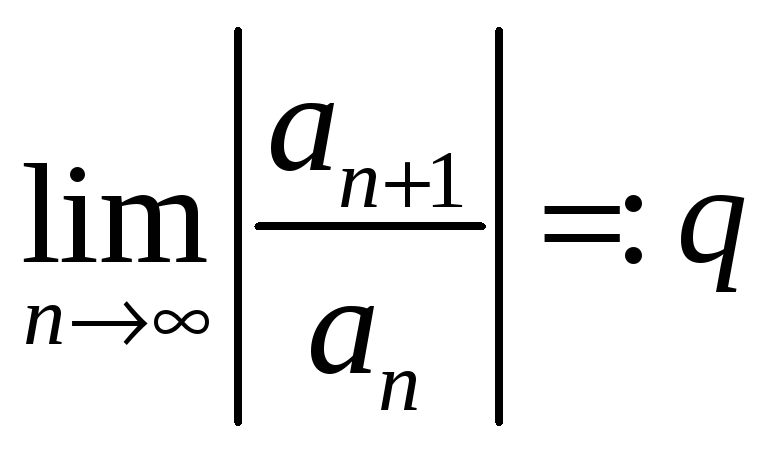, то радиус сходимости степенного ряда будет равен или .

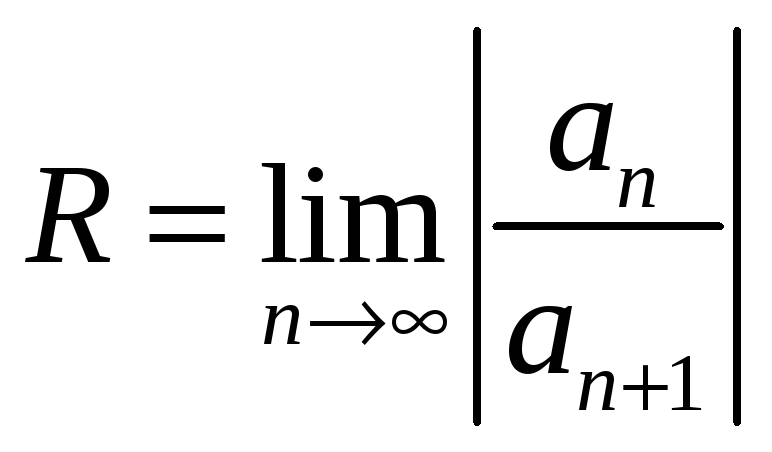Примеры:

1)

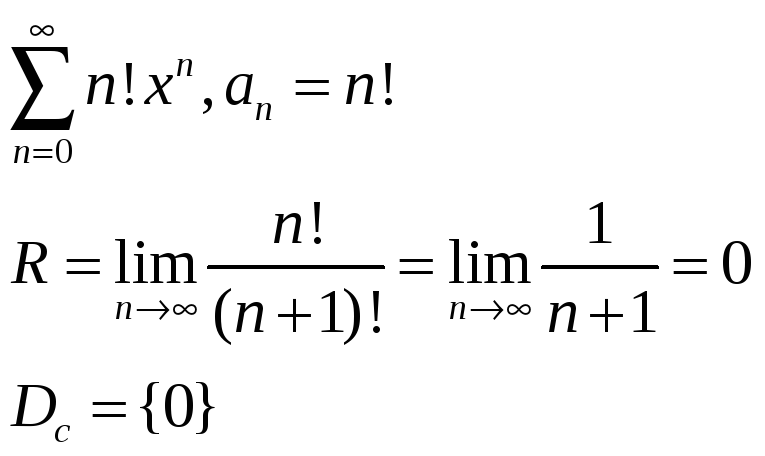
2)

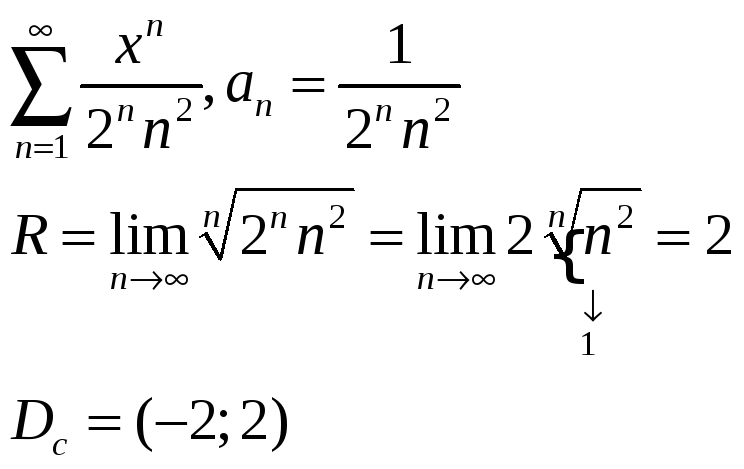
Исследуем поведение ряда в концевых точках

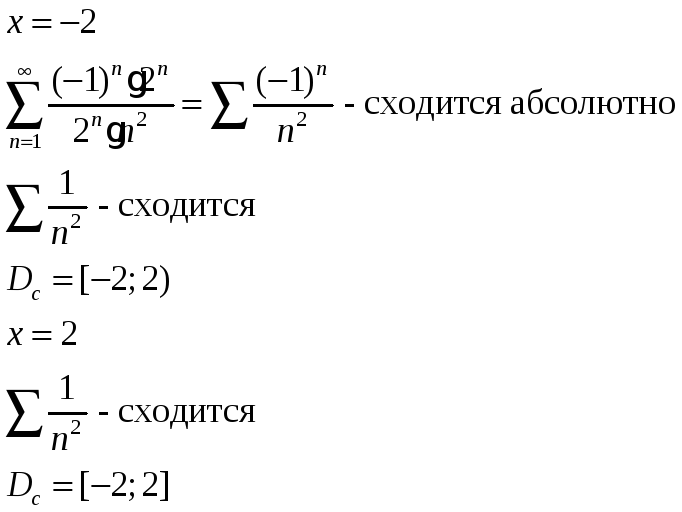
ряд сходится абсолютно.

Свойства степенных рядов:

Теорема 1. (о почленном интегрировании).

Степенной ряд можно почленно интегрировать в интервале сходимости, т.е. для любого числа существует интеграл (3).

Ряд (3) называют проинтегрированным рядом; по отношению к исходному ряду (1) ряд (3) тоже является степенным с радиусом сходимости . Ряд (3) сходится во всех точках области сходимости исходного ряда, т.е. .

Пример:

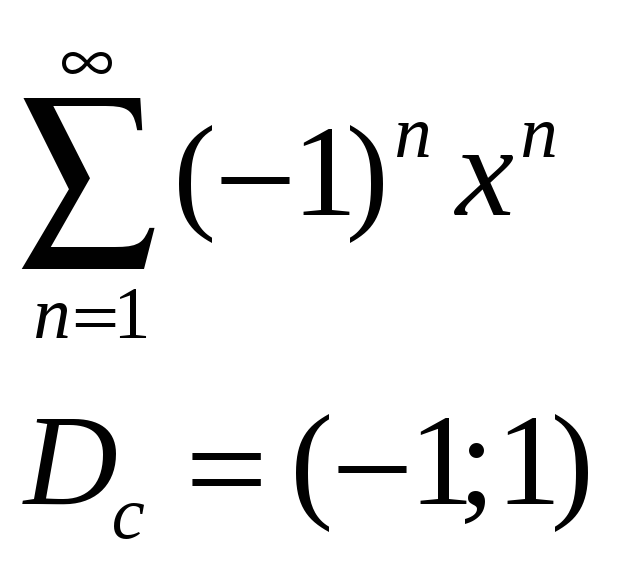
Проинтегрируем данный ряд:

Теорема 2 (о почленном дифференцировании).

В ( - внутренняя точка области сходимости) степенной ряд допускает почленное дифференцирование, причем (4).

Ряд (4) называют продифференцированным рядом и .

Следствие: степенной ряд внутри промежутка сходимости допускает почленное дифференцирование любое количество раз.

Пример: найти сумму ряда

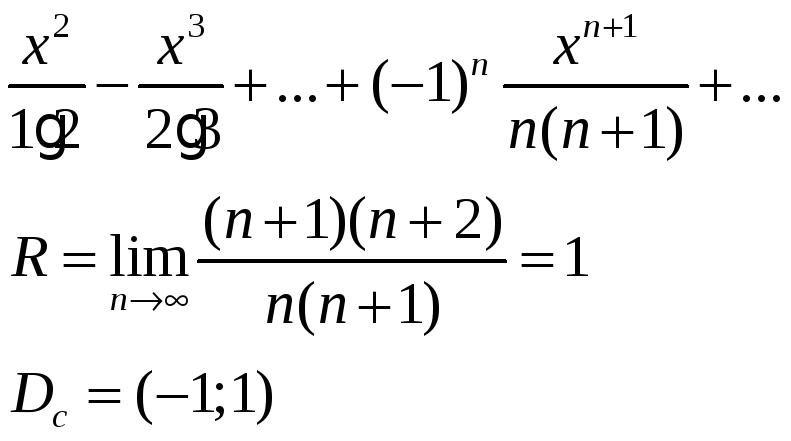
при ряд

Продифференцировав данный ряд, получим:

еще раз продифференцируем

Т.к.

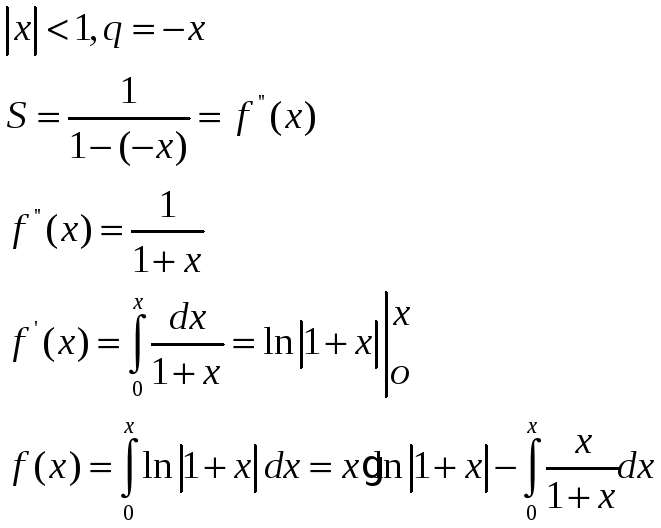
§3.3. Разложение функции в степенные ряды.

Частичные суммы степенного ряда представляет собой многочлены, так что легко вычисляются. Поэтому удобно при возможности представить функцию в виде суммы степенного ряда (или, как говорят, разложить функцию в ряд).

Пусть разложима в степенной ряд, т.е. существуют коэффициенты и точка , такие, что (1).

Ясно, что в этом случае, если некоторой промежуток - область сходимости, то внутри этого промежутка степенной ряд можно бесконечно дифференцировать, поэтому необходимым условием разложения функции в степенной ряд в промежутке является бесконечная дифференцируемость в .

Пусть есть и разложима в ряд (1), тогда согласно теореме о бесконечной дифференцируемости степенного ряда для имеем:

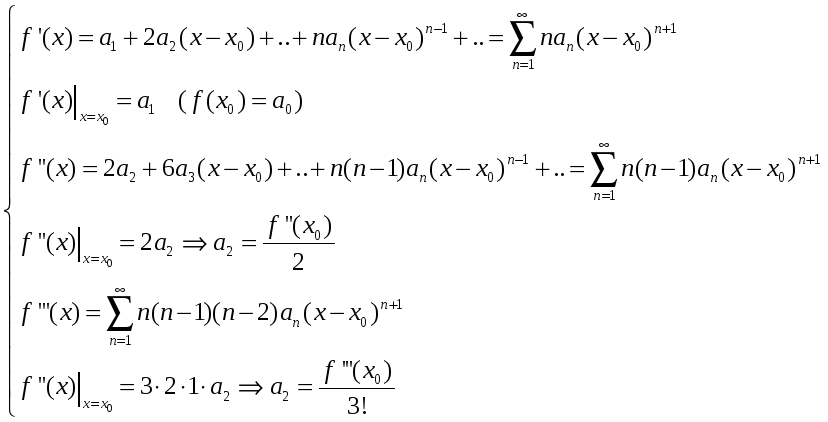
Продолжая процесс, получаем:

(2)

Таким образом, ряд, который разлагается, функция необходимый имеет вид:

(3)

(3) – ряд Тейлора для функции с центром в точке .

Ясно, что для любой функции, бесконечно дифференцируемой в точке , ряд Тейлора всегда существует. Сходимость же этого ряда надо исследовать.