3.6. Абстрактні автомати

Абстрактний автомат — це алгоритмічна система, яку визначають три множини: вхідний алфавіт Х, вихідний алфавіт У, множина внутрішніх станів автомата S, а також дві функції (функція переходів та функція виходів). Щоб задати абстрактний автомат, є такі способи: функціональний, за допомогою таблиць переходів та виходів і графічний (залежно від способу задання функцій).

Функціональний спосіб задання абстрактних автоматів.

Автомат працює у дискретному часі. Послідовні моменти часу ототожнюють із послідовними натуральними числами t = 0, 1, 2 ... (це завжди можна зробити, обравши за одиницю часу будь-який зручний відрізок виміру).

У кожний момент автоматного часу t = 0, 1, 2 ... автомат А знаходиться у деякому стані S(t)  S. Початковий стан автомата А — S(0).

У кожний момент часу t, починаючи з t = 1, до входу автомата надходить одна літера x(t)  X вхідного алфавіту (вхідний сигнал). Вхідними словами автомата будуть скінченні впорядковані послідовності вхідних сигналів x(1) x(2) ... x(k). Кожний автомат має множину припустимих вхідних слів. Будь-яке припустиме слово p = x(1) x(2)... x(k), що подане до входу автомата, викликає появу вихідного слова q = y(1)y(2) ... y(k) — впорядкованої послідовності вихідних сигналів автомата А тієї самої довжини.

Відповідність між припустимими вхідними словами p і вихідними словами q називають алфавітним відображенням, індукованим автоматом А. Це відображення однозначно задається двома функціями — функцією переходів з одного стану в інший та функцією виходів, що визначає вихідний символ або сигнал.

Стан автомата S(t) у будь-який момент часу t однозначно визначається попереднім станом S(t-1) та вхідним сигналом x(t). Але щодо моменту часу t переходу зі стану S(t-1) у стан S(t), вихідний сигнал y(t) може з’явитися або до переходу, або після нього. Тому y(t) може бути визначений двома способами:

Функція  є функцією виходів. Причому  * — це звичайна функція, яка визначає вихідну літеру y(t) залежно від вхідного сигналу x(t) в момент t та від стану y попередній момент часу S(t–1), ** — функція зсунута, яка визначає вихідну літеру y(t) залежно від стану s(t) в момент часу t і вхідного сигналу x(t) в той самий момент часу t.

Залежно від визначення y(t) розрізняють два типи абстрактних автоматів:

— це автомат I роду, або автомат Мілі,

— це автомат II роду, або автомат Мура.

Якщо всі три множини X, Y, S, що визначають абстрактний автомат А, є скінченними, то й автомат називають скінченним.

Табличний спосіб задання абстрактного автомата.

Абстрактний автомат можна задати за допомогою двох таблиць: таблиці переходів та таблиці виходів автомата. Рядки обох таблиць позначаються символами вхідного алфавіту Х, а стовпчики — символами станів. На перетині Х-го рядка та S-го стовпчика таблиці переходів стоїть елемент U(s, x), тобто деякий символ вихідного алфавіту Y.

Розглянемо приклад.

Нехай маємо скінченний автомат Мілі, заданий трьома множинами S = {1, 2, 3}; X = {a, b}; Y= {u, v}.

Нехай він функціонує за такими таблицями:

Якщо до входу автомата Мілі буде подано слово aabb, то на виході матимемо слово uvuu.

Якщо задано автомат Мура (II роду) тими самими множинами S, X, Y, то його об’єднана таблиця виходів та переходів матиме вигляд:

Різниця між двома класами автоматів полягає у тому, що у випадку автоматів Мілі вихідний сигнал виникає одночасно із вхідним сигналом, що його індукує, а у випадку автоматів Мура — із затримкою на 1 (одиницю) автоматного часу.

Абстрактний автомат може мати область заборони, або сукупність слів у вхідному алфавіті, які не сприймаються автоматом, що знаходиться у деяких станах з множини станів, тобто у якомусь стані, автомат не сприймає певний вхідний символ (ситуація схожа з діленням на 0). Тоді у таблицях переходів та виходів у відповідних клітинах стоятиме «–». Так би мовити, аварійний вихід (зупинка).

Графічний спосіб задання автомата.

Другим способом задання абстрактного автомата є графічний — він більш наочний і використовує графи. Вершини графа (у вигляді кола) ототожнюються зi станами автомата. Стрілка, що з’єднує вершину i з вершиною j, означає, що існує вхідний сигнал x, який переводить автомат зi стану i у стан j , тобто j = (i, х). Той самий автомат за допомогою граф-схеми зображено на рис. 3.4.

Рис. 3.4. Представлення автомата за допомогою граф-схеми

Графи

Граф автомат - це орієнтований зв'язний граф, вершини якого символізують внутрішні стани автомата, а дуги - переходи з одного стану в інший.

Для графа Мілі на дугах вказуються вхідні і вихідні букви. Вихідні букви пишуться над дугами, символізуючи те, що вихідний стан залежить від стану автомата в попередній момент часу.

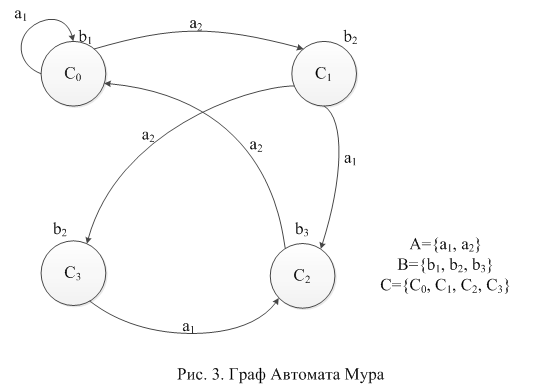
Для графа автомата Мура на дугах записуються тільки вхідні букви, вихідні ж вказуються біля вершин.

Важливий момент: Якщо з кожної вершини виходить стільки дуг, скільки є вхідних букв, то автомат називається повним. Іншими словами - якщо з кожної вершини визначені переходи для кожної вхідної букви. У наших прикладах автомат Мілі є повним, а автомат Мура - частковим.

Якщо з однієї вершини виходить дуг більше, ніж вхідних букв (тобто 2 і більше дуг з однаковими вхідними буквами), то такий автомат називається недетермінованим, інакше - детермінованим автоматом.