6.3. Кластерный анализ

Метод кластерного анализа позволяет строить классификацию n объектов посредством объединения их в группы, или кластеры, на основе критерия минимума расстояния в пространстве m показателей, описывающих объекты. Вероятностное обоснование результатов кластеризации можно получить методом дискриминантного анализа.

Исходные данные для кластерного анализа представляются в виде матрицы размером tхn, содержащей информацию трех типов, но на практике чаще всего используют один тип — измерения x_ij значений t показателей для n объектов. При этом если исходные данные представляют собой значения показателей и переменных для некоторого объекта, то необходимо выбрать стратегию объединения и метод вычисления расстояния d_ij между объектами в многомерном пространстве показателей — мeтрику. Метрика —способ определения расстояний между двумя точками ( объектами ).

При выполнении анализа расстояние между объектами

оценивают с помощью следующих различных метрик:

• евклидовой метрики ( данная метрика применяется для переменных, измеренных в одних единицах);

• нормализованной евклидовой метрики (эта метрика подходит для переменных, измеренных в различных единицах);

• метрики суммы квадратов (может использоваться в случае, когда расстояние между кластерами равно сумме расстояний между их компонентами);

• взвешенных суммированных квадратов (этот вид метрики применяют, когда переменные имеют различную значимость, при этом матрица данных должна содержать веса показателей);

• манхеттеновской метрики (применяется для ранговых переменных);

• метрики Брея-Картиса (применяется для ранговых данных, имеющих значения от 0 до 1 ).

Дивизивная стратегия динамических сгущений позволяет сгруппировать объекты в заданное число кластеров. Промежуточным результатом анализа является среднее внутрикластерное расстояние, по которому можно сравнить различные варианты кластеризации, и кластеры с указанием включенных в них объектов. При этом можно получить проекции на плоскость каждой пары показателей, центров кластеров и объектов каждого кластера, соединенных линиями с центрами.

Агломеративные стратегии позволяют строить дендрограмму классификации в ходе построения иерархии объединения кластеров. Часто используют следующие варианты этой стратегии:

• стратегия ближайшего соседа очень сильно сжимает пространство исходных и позволяет получить минимальное дерево групповой классификации;

• стратегия дальнего соседа сильно растягивает пространство;

• стратегия группового соседа сохраняет матрицу пространства;

• гибкая стратегия – универсальна и зависит от значения бета-

параметра, который должен быть меньше 1; при бета=0 метрика не меняется, при бета >0 пространство сжимается; при бета <0 —растягивается;

• метод Уорда минимизирует внутрикластерный разброс объектов.

В результате применения этой стратегии получают

матрицы расстояния между объектами, последовательности кластеров возрастающей общности с указанием входящих в кластеры объектов и расстояния между ними, на уровне которых произошло объединение кластеров, а также дендрограмму – дерево объединения кластеров.Рассмотрим на примере проведение классификации 10 предприятий по двум показателям ( данные табл. 6.11) .

Таблица 6.11

Показатели структуры активов предприятий

Номер предприятия	1	2	3	4	5	6	7	8	9	10
Доля наиболее ликвидных активов Доля запасов	0,27 0,40	0,32 0,39	0,20 0,46	0,27 0,39	0,34 0,30	0,20 0,39	0,22 0,42	0,22 0,52	0,21 0,51	0,23 0,42

Для решения поставленной задачи используем пакет статистической программы STADIA 5.0.Введем показатели 10 предприятий в 10 строк электронной таблицы, в первый столбец – долю наиболее ликвидных активов в валюте баланса, а во второй – долю запасов в валюте в балансе.

Используя процедуру « Кластерный анализ», команды и соответственно метод «Дивизивная стратегия динамических сгущений» и «Евклидова метрика» сгруппируем предприятия в два кластера .

На рис.6.1 приведено графическое изображение этих кластеров в координатах двух рассмотренных показателей. В результате анализа оказалось, что группировка предприятий в два кластера возможна, первый кластер включает предприятия № 3,6,7,8,9,10 ; второй – 1,2,3,4,5.

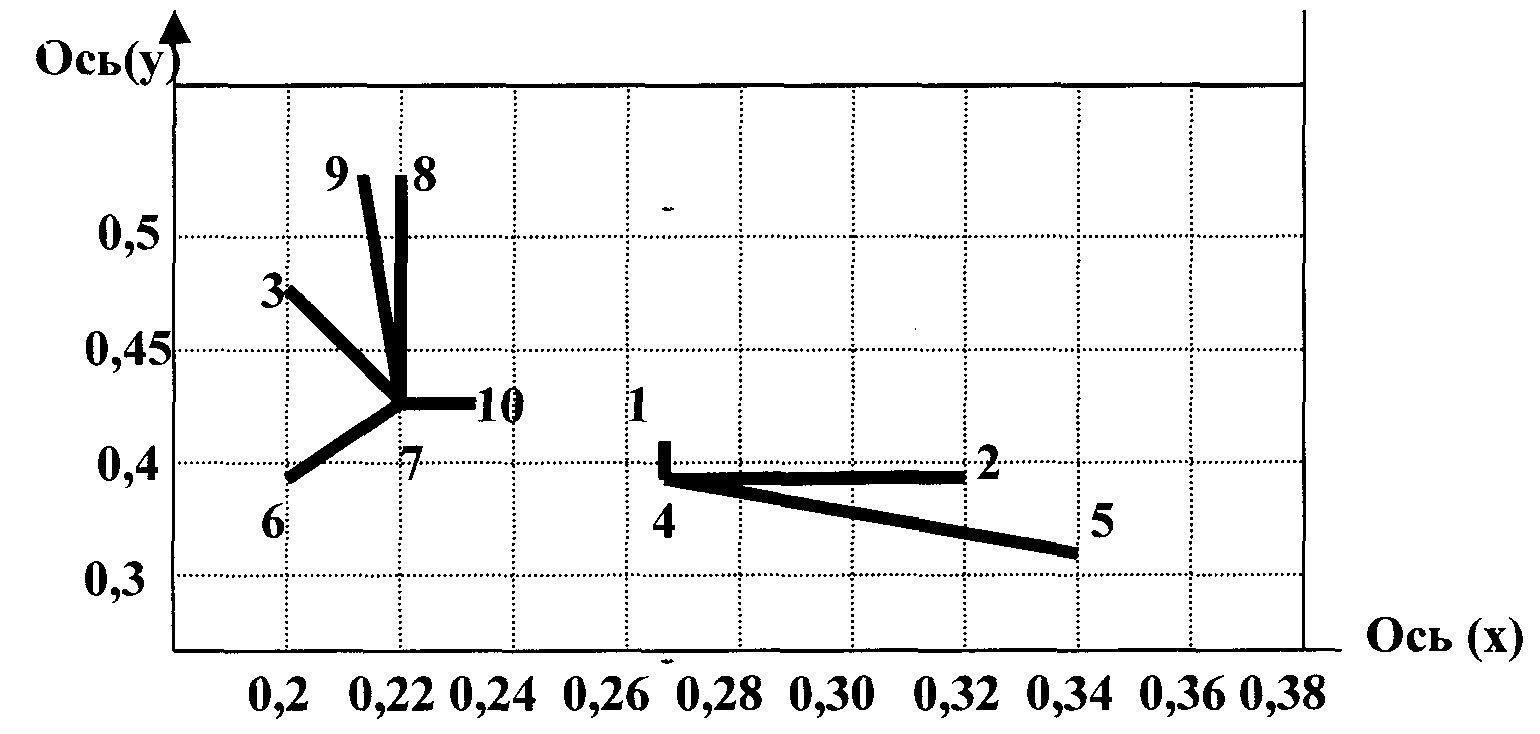
Рис.6.1. Изображение двух кластеров в плоскости показателей структуры балансов предприятий

При небольшом количестве показателей получение кластеров возможно с помощью метода группировки. Для решения поставленной выше задачи с помощью метода группировки необходимо определить шаг первого показателя.

В нашем примере .

В табл. 6.12 приведена группировка предприятий по показателям структуры активов.

Таблица 6.12

Группировка предприятий по структуре активов

Величина интервала	Количество предприятий	Номер предприятия
0,2-0,27	6	3,6,7,8,9,10
0,27-0,34	4	1,2,4,5
Итого	10

Результаты анализа кластерным методом и методом группировок совпадают. Однако в тех случаях, когда как объектов, так и показателей множество, применение метода группировок для анализа классификаций невозможно. В этом случае используется кластерный метод.