5.4. Регрессионный анализ

Изучение корреляционных зависимостей основывается на исследовании таких связей между показателями, при которых значения результативного показателя «в среднем» изменяются в зависимости от того, какие значения принимают факторы. Действие факторов осуществляется в условиях сложного их взаимодействия , вследствие чего проявление закономерности затемняется влиянием случайностей. Вычисляя средние значения результативного показателя для данной группы значений фактора, мы отчасти элиминируем значение случайностей. Вычисляя параметры теоретической линии связи, производим дальнейшее их элиминирование и получаем однозначное (по форме) изменение y с изменением фактора x.

Теоретической линией регрессии называется та линия, вокруг которой группируются точки корреляционного поля и которая указывает основное направление, основную тенденцию связи. Теоретическая линия регрессии должна отображать изменение средних величин результативного признака y по мере изменения величин факторного признака x при условии полного взаимопогашения всех прочих – случайных по отношению к фактору x – причин. Следовательно, эта линия должна быть проведена так, чтобы сумма отклонений точек поля корреляции от соответствующих точек теоретической линии регрессии равнялась нулю, а сумма квадратов этих отклонений была минимальной величиной.

Важным этапом регрессионного анализа является определение типа функции, с помощью которой характеризуется зависимость между признаками. Главным основаним для выбора вида уравнения должен служить содержательный анализ природы изучаемой зависимости, ее механизма. Вместе с тем теоретически обосновать форму связи каждого из факторов с результативным показателем можно далеко не всегда, поскольку на основе теоретического анализа нередко могут быть сделаны самые общие выводы относительно направления связи, правомерности использования линейной зависимости, возможного наличия экстремальных значений и т. п. Необходимым дополнением такого рода предположений должен быть анализ конкретных фактических данных.

Приблизительное представление о линии связи можно получить на основе эмпирической линии регрессии. Эмпирическая линия обычно является ломаной линией. Объясняется это тем, что влияние прочих неучтенных факторов, оказывающих воздействие на изменение результативного показателя, в средних погашается не полностью в силу недотаточно большого количества наблюдений. Эмпирической линией связи для выбора и обоснования типа теоретической кривой воспользоваться только при условии, что число наблюдений достаточно велико.

Можно также использовать опыт предыдущих исследований и там, где выбранные формы уравнений связи давали удовлетворительный результат, можно рекомендовать их использовать и в дальнейшем.

Наиболее часто для характеристики связей экономических показателей используют следующие типы функций:

линейную ,

гиперболическую ,

показательную ,

параболическую ,

степенную ,

логарифмическую ,

логистическую .

В рассматриваемом примере эмпирическая линия регрессии все же больше всего приближается к прямой, и, следовательно, теоретическая линия регрессии может быть представлена уравнением вида:

.

Для нахождения параметров a и b уравнения регрессии используем метод наименьших квадратов. Система нормальных уравнений способа наименьших квадратов для определения величины параметров a и b уравнения прямолинейной корреляционной связи по эмпирическим данным имеет вид:

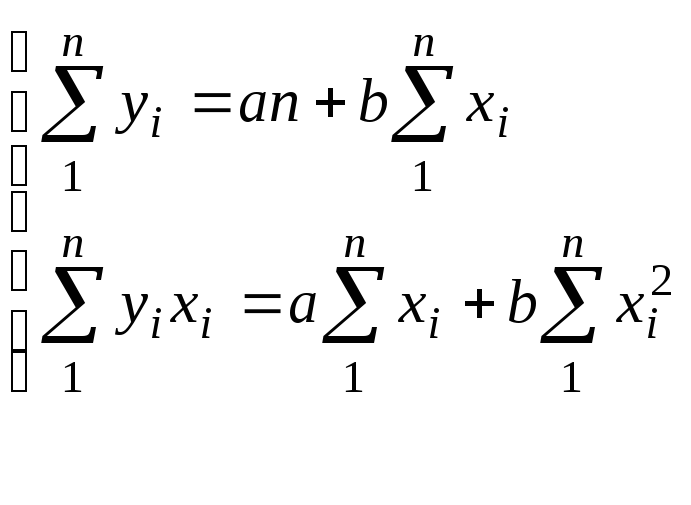(5.6)

Используя результаты расчетов в п. 5.3, можно записать для нашего примера систему нормальных уравнений :

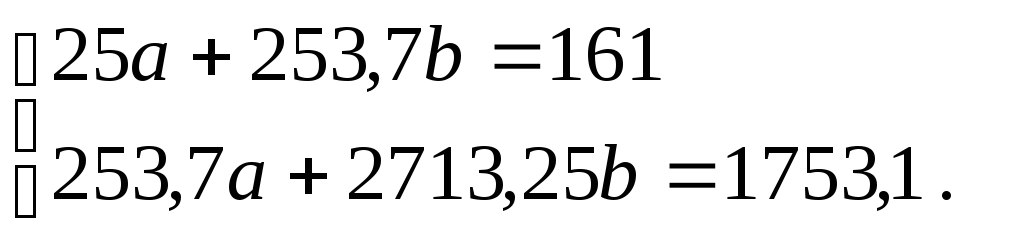
В результате решения получим:

a=-2,25 b=0,857 и

Параметр b в уравнении называют коэффициентом регрессии. При наличии прямой корреляционной зависимости коэффициент регрессии имеет положительное значение, а в случае обратной зависимости коэффициент регрессии – отрицательный.

Коэффициент регрессии показывает, насколько в среднем изменяется величина результативного признака y при изменении факторного признака x на единицу. Геометрически коэффициент регрессии представляет собой наклон прямой линии, изображающей уравнение корреляционной зависимости относительно оси x ( для уравнения ).

Коэфициент регрессии применяют для определения коэфициента эластичности, который показывает, на сколько процентов изменится величина результативного признака y при изменении фактора x на один процент.

Для определения коэффициента эластичности используется формула:

(5.7)

Для нашего примера коэффициент эластичности будет равен:

Это означает, что при росте энерговооруженности на 1 % производительность труда возрастает на 1,3 %.

Степень близости выбранной теоретической линии к фактическим данным характеризует индекс корреляции. Этот показатель может находиться в пределах от 0 до 1 и определяется по формуле:

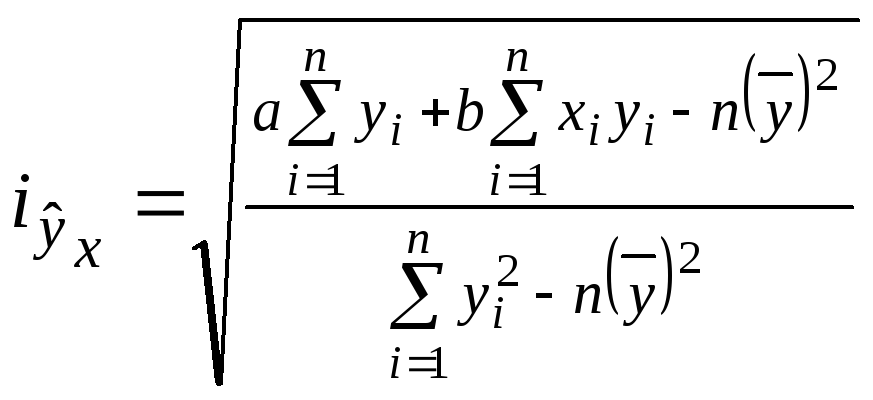(5.8)

Если равен или близок к нулю, это означает, что между показателями х и y нет связи, или если она и существует, то не может быть охарактеризована выбранной формой уравнения регресcии.

Для рассматриваемого примера индекс корреляции составляет:

Близость величины к единице в общем случае означает, что связь между показателями достаточно хорошо описывается избранным уравнением зависимости. Для рассматриваемого примера это означает, что выбор линейной функции в качестве уравнения регрессии достаточно обоснован.