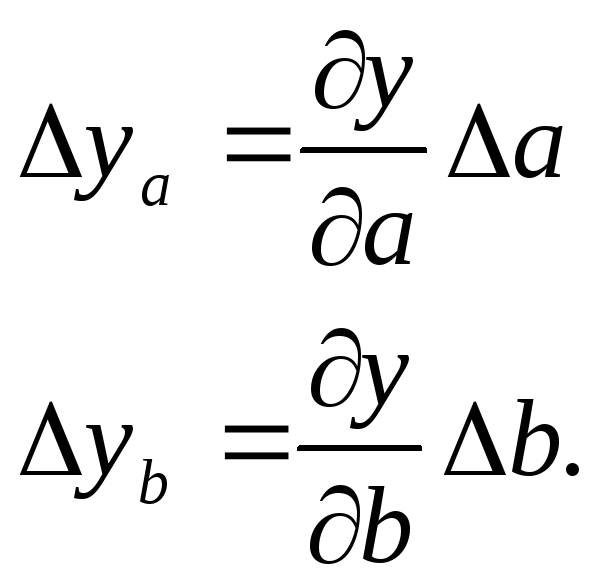- •Краткие сведения из истории развития экономического анализа
- •1.2. Содержание, предмет и задачи экономического анализа
- •Решение перечисленных выше задач обеспечивает достижение основной цели экономического анализа, которая состоит в содействии эффективному развитию предприятий.
- •1.3. Метод экономического анализа и его особенности
- •1.4. Виды экономического анализа
- •1.5. Система экономической информации и методы ее обработки
- •1.6. Способы сопоставимости показателей
- •1.7 Классификация способов и приёмов экономического анализа
- •Глава 2. Традиционные способы обработки экономической информации
- •2.1 Прием группировки аналитической информации
- •2.2 Прием сравнения аналитических данных
- •2.3. Абсолютные, относительные и средние величины в анализе
- •2.4. Табличный способ отражения аналитических данных
- •Анализ состава населения по полу и образованию
- •Анализ состава населения по полу и образованию
- •Графический способ
- •Глава 3. Факторы и резервы в экономическом анализе
- •3.1. Понятие, типы и задачи факторного анализа
- •3.2 Классификация и систематизация факторов в экономическом анализе
- •3.3. Понятие, экономическая сущность хозяйственных резервов и их классификация
- •3.4. Принципы организации поиска резервов
- •3.5. Методика подсчета и обоснования величины резервов
- •Этот же расчет интегральным способом:
- •Глава 4. Детерминированное моделирование и анализ факторных систем
- •4.1. Постановка задачи прямого детерминированного факторного анализа. Методы моделирования факторных систем
- •Комбинированные модели представляют собой сочетание в различных комбинациях рассмотренных выше моделей. Примерами таких моделей могут быть:
- •Метод дифференциального исчисления
- •4.3. Метод цепных подстановок
- •4.4. Метод абсолютных разниц
- •Cпособ относительных разниц
- •4.6. Индексный метод
- •4.7. Интегральный метод
- •Вычислив все интегралы, получим матрицу :
- •4.8 Логарифмический метод
- •Глава 5. Стохастический факторный анализ
- •5.1. Особенности и предпосылки стохастического анализа
- •5.2. Методы выявления наличия корреляционной связи между двумя показателями
- •Исходные данные
- •Групповая таблица
- •5.3. Измерение степени тесноты корреляционной связи в случае парной зависимости
- •5.4. Регрессионный анализ
- •5.5. Множественная корреляция
- •5.6. Построение и исследование экономико-математических моделей с помощью корреляционного анализа
- •Проверка достоверности полученной модели.
- •Расчетные данные для определения парных коэффициентов корреляции
- •Расчетные данные для определения парных коэффициентов корреляции
- •Глава 6. Способы решения задач обратного факторного анализа
- •6.1. Понятие комплексной оценки хозяйственной деятельности предприятия
- •6.2. Методы детерминированной комплексной оценки
- •Комплексная оценка методом балльной оценки
- •6.3. Кластерный анализ
- •6.4 . Дискриминантный анализ
- •Глава 7. Перспективный анализ
- •7.1. Роль перспективного анализа в управлении предприятием
- •7.2. Методы моделирования одномерных временных рядов
- •7.3. Моделирование и обнаружение тенденции временного ряда
- •7.4. Адаптивные модели краткосрочного прогнозирования
- •Глава 8 . Экономико-математические методы в анализе
- •8.1. Значение математических методов в управлении предприятием, их общая характеристика
- •8.2. Применение методов линейного программирования в решении ряда задач
- •8.3. Решение аналитических задач с помощью методов теории вероятностей и математической статистики
- •8.5. Реализация состояний станков участка
- •8.4. Методы анализа эффективности управления запасами
- •8.5. Метод монте-карло
- •8. 6. Дисперсионный анализ
- •8.7. Экспертные методы
- •Ранжирование объектов методом попарного сравнения
- •Глава 9.
- •9.1 Содержание, задачи и формы фса
- •9.2. Основные методы фса в сфере производства
- •9.3. Функционально-стоимостный анализ в сфере проектирования
- •Часть 9
- •9.4. Функционально - стоимостный анализ при проектировании изделий
- •Содержание функций и их материальные носители
- •Показатели использования оборудования
- •Коэффициенты отказов и простоев
- •Показатели технического состояния
- •Общие производственные потери
- •Расчетные данные о полезном объеме выполненных
- •Глава 10.
- •10.1. Организация аналитической работы
- •10.2. Организация экономического анализа в автоматизированной системе управления
- •10.3. Классификация информации для анализа хозяйственной деятельности
- •10.4. Информационное обеспечение экономического анализа и его структура
- •10.5. Проверка достоверности информации и ее аналитическая обработка
- •Литература
- •Приложение 5 Случайные числа
- •Необходимое число объектов наблюдения при нормальном распределении
- •Глава 1. Введение в методологию экономического 5
- •Глава 2. Традиционные способы обработки экономической 30 информации
- •Глава 3. Факторы и резервы в экономическом анализе 72
- •Глава 4. Детерминированное моделирование и анализ 90
- •Глава 5. Стохастический факторный анализ 132
- •Глава 6. Способы решения задач обратного факторного анализа 170
- •Глава 7. Перспективный анализ 193
- •Глава 8. Экономико-математические методы в анализе 208
- •Глава 9. Функционально стоимостной анализ 275
- •Глава 10. Организация анализа и его информационная база 330
- •Министерство образования и науки украины
- •Теория экономического анализа
-
Метод дифференциального исчисления
Метод дифференциального исчисления является теоретической основой количественной оценки влияния отдельных факторов на изменение результативного (обобщающего) показателя. В основу метода положена формула Тейлора:
|
|
(4.5) |
где f – функция; хi – факторы; ρ – евклидова норма вектора приращения факторов; 0(ρ) – функция бесконечно малая, порядка выше ρ, т.е. убывающая при ρ → 0 быстрее, чем ρ.
При использовании этого метода предполагается, что общее приращение функции (результативного признака) раскладывается на слагаемые. Значение каждого из слагаемых (кроме последнего) определяется умножением соответствующей частной производной (взятой при начальных значениях факторов) на изменение фактора, по которому вычислена данная производная. Если функция у=f(a,b) дифференцируема, то используя формулу Тейлора, ее приращение можно выразить как:
|
|
(4.6) |
где Δу=у1-у0 — изменение функции (результативного показателя);
Δа =а1-а0 — изменение фактора а;
Δb = b1-b0 — изменение фактора b;
0(![]() )
— бесконечно малая величина (остаточный
член или логическая ошибка метода
дифференцирования) более высокого
порядка, чем (
)
— бесконечно малая величина (остаточный
член или логическая ошибка метода
дифференцирования) более высокого
порядка, чем (![]() ).
).
Таким образом, влияние факторов а и b на изменение результативного показателя определится по формулам:
|
|
|
Cумма
Δуа
и Δуb
представляет собой главную, линейную
относительно приращения факторов часть
приращения дифференцируемой функции.
Параметр 0(![]() )
мал при достаточно малых изменениях
факторов, при значительных изменениях
переменных остаточный член может
существенно отличаться от нуля.
)
мал при достаточно малых изменениях
факторов, при значительных изменениях
переменных остаточный член может
существенно отличаться от нуля.
Рассмотрим применение метода дифференцирования в решении задачи прямого детерминированного факторного анализа для двухфакторной мультипликативной модели.
Необходимо определить влияние факторов на изменение объема товарной продукции. Значения результативного показателя и факторов приведены в таблице 4.1
Таблица 4.1
Исходные данные для факторного анализа
|
Наименование показателей |
Начальный период |
Конеч ный период |
Абсолют ное отклонение |
|
1.Объем товарной продукции, тыс. грн. (у) |
1020 |
927 |
-93 |
|
2.Численность рабочих, чел. (а) |
100 |
90 |
-10 |
|
3.Средняя выработка одного рабочего за период, тыс.грн. (b) |
10.2 |
10.3 |
+0.1 |
Условием задачи задана мультипликативная двухфакторная система у=аb. Определим влияние факторов на изменение объема товарной продукции.
Влияние изменения численности рабочих на изменение объема товарной продукции :
Δуа=b0∆a=10,2x(-10)= -102 тыс.грн.
Влияние изменения средней выработки одного рабочего на изменение объема товарной продукции :
Δуb=a0Δb=100x0,1=10 тыс. грн.
Легко доказать, чему равен остаточный член равенства:
0
(![]() )=
Δу
- Δуа+
Δуb=(a1b1
–a0b0)
- b0
∆a-
a0
Δb=(
a1b1
–a0b0)
- b0
(a1-a0)-
)=
Δу
- Δуа+
Δуb=(a1b1
–a0b0)
- b0
∆a-
a0
Δb=(
a1b1
–a0b0)
- b0
(a1-a0)-
a0 (b1-b0)= a1b1 – a0b0 – a1b0+a0b0 – a0b1 +a0b0 = a1(b1-b0)- a0(b1-b0)=(a1-a0)(b1-b0)=∆a∆b.
Таким образом, в данной задаче величина остаточного члена или т.н. неразложимого остатка равна:
∆a∆b= - 10 х 0,1= -1тыс.грн.
Баланс отклонений:
Δу = Δуа+ Δуb + ∆a∆b= -102+10 –1= -93 тыс.грн.
По результатам решения задачи можно сделать вывод, что объем товарной продукции за анализируемый период уменьшился на 93 тыс.грн. На изменение результативного показателя факторы оказывали разнонаправленное действие. Так, при уменьшении численности рабочих на 10 человек объем товарной продукции уменьшился на 102 тыс.грн. Рост выработки одного рабочего на 0.1 тыс.грн за анализируемый период позволил увеличить объем товарной продукции на 10 тыс.грн. Следовательно, уменьшение объема товарной продукции было вызвано уменьшением величины экстенсивного фактора (численности рабочих).
В методе дифференцирования неразложимый остаток, который интерпретируется как логическая ошибка данного метода, вносит погрешность при определении величин влияния факторов. В этом состоит неточность рассматриваемого метода.