
- •Введение
- •1. Общие рекомендации студенту-заочнику по работе над курсом высшей математики
- •2. Правила выполнения и оформления контрольных работ
- •3. Программа
- •3.1. Элементы линейной алгебры и аналитической геометрии
- •3.2. Введение в математический анализ
- •3.3. Дифференциальное исчисление функций одной переменной
- •3.4. Применение дифференциального исчисления для исследования функций и построения их графиков
- •4. Линейная алгебра и аналитическая геометрия
- •4.1. Матрицы
- •4.2. Системы линейных уравнений. Матричный метод. Правило Крамера. Метод Гаусса
- •4.3. Скалярное произведение векторов в r3
- •4.4. Векторное произведение векторов
- •4.5. Смешанное произведение векторов
- •4.6. Прямая на плоскости. Плоскость
- •1. Прямая на плоскости.
- •4.7. Линии второго порядка
- •4.8. Поверхности второго порядка
- •5. Введение в математический анализ
- •5.1. Предел числовой последовательности. Предел функции
- •5.2. Бесконечно малые и бесконечно большие функции Сравнение бесконечно малых. Непрерывность функции. Точки разрыва и их классификация
- •6. Дифференциальное исчисление функций одной переменной
- •6.1. Дифференцирование функций
- •6.2. Производные и дифференциалы высших порядков. Дифференцирование функций, заданных параметрически
- •6.3. Приложение теорем Ролля, Лагранжа, Коши. Правило Лопиталя
- •6.4. Формула Тейлора и ее приложения
- •7.2. Исследование функций и построение их графиков
- •Контрольная работа № 1
- •Литература
7.2. Исследование функций и построение их графиков
Исследование функций и построение их графиков удобно выпол-нять по следующей схеме.
-
Найти область определения функции.
-
Выяснить, является ли функция четной, нечетной, периодической.
-
Исследовать функцию на непрерывность, найти точки разрыва.
-
Найти асимптоты графика функции.
-
Установить интервалы монотонности функции. Найти точки экстремума функции, вычислить значения функции в этих точках.
-
Определить интервалы выпуклости и вогнутости графика функции, точки перегиба.
-
Используя результаты проведенного исследования, построить график функции. При необходимости уточнения отдельных участков кривой можно вычислить координаты нескольких дополнительных точек (в частности, координаты точек пересечения графика с осями координат).
Пример
7.4. Исследовать функцию
![]() и построить ее график.
и построить ее график.
Функция определена
и непрерывна на всей оси, кроме точек
![]() .
.
Функция нечетная,
так как
![]() ,
ее график симметричен относительно
начала координат, поэтому достаточно
исследовать функцию для
,
ее график симметричен относительно
начала координат, поэтому достаточно
исследовать функцию для
![]() .
Прямые х
=
–2 и х
=
2 являются
вертикальными асимптотами, поскольку
.
Прямые х
=
–2 и х
=
2 являются
вертикальными асимптотами, поскольку
![]() .
Найдем наклонные асимптоты
.
Найдем наклонные асимптоты
![]() :
:
![]() ;
;
![]() .
.
Следовательно,
![]() – наклонная асимптота.
– наклонная асимптота.
Производная
функции
![]() обращается в нуль при
обращается в нуль при
![]() и
и
![]() .
.
Вторая производная
![]()
обращается в нуль
при
![]() .
.
Составим таблицу
|
х |
0 |
(0; 2) |
2 |
(2;
|
|
( |
|
|
0 |
+ |
Не сущ. |
+ |
0 |
– |
|
|
0 |
+ |
Не сущ. |
– |
– |
– |
|
у |
0 |
|
Не сущ. |
|
|
|
Следовательно,
![]() – точка максимума,
– точка максимума,
![]() .
В
силу нечетности имеем:
.
В
силу нечетности имеем:
![]() – точка минимума
– точка минимума
![]() .
Поскольку
.
Поскольку
![]() при
при
![]() и
и
![]() при
при
![]() ,
то х
=
0 – абсцисса
точки перегиба, 0(0;0) – точка перегиба.
,
то х
=
0 – абсцисса
точки перегиба, 0(0;0) – точка перегиба.
Используя полученные данные, строим график функции (рис. 7.1).
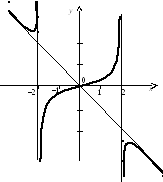
Рис. 7.1
Контрольная работа № 1
1 – 20. Решить системы по формулам Крамера, матричным способом и методом Гаусса.
1.
 2.
2.
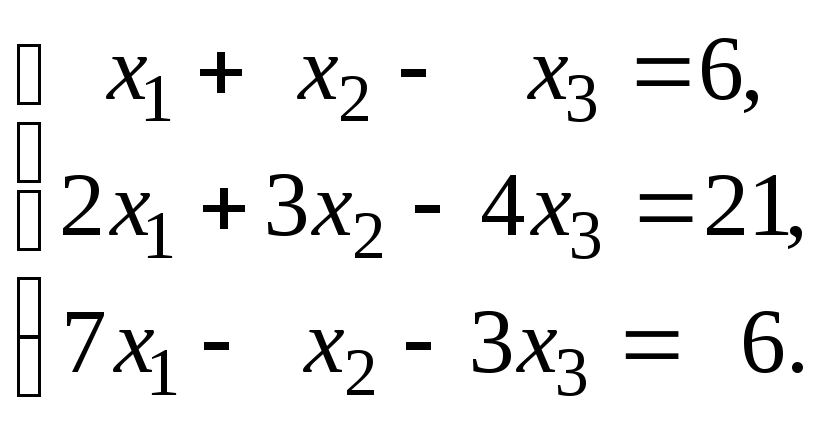
3.
 4.
4.
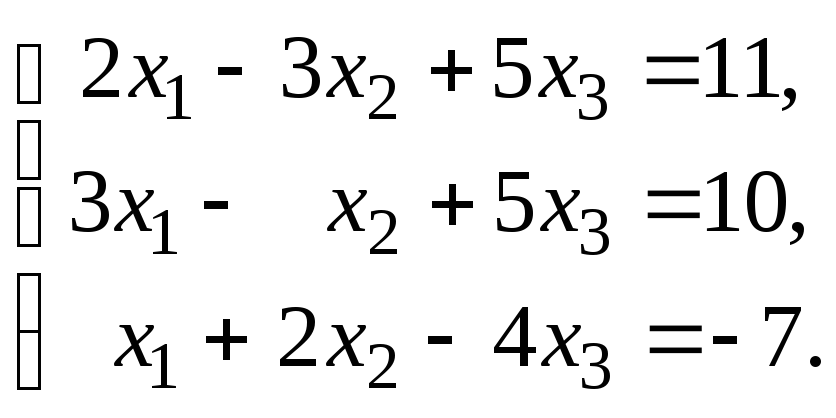
5.
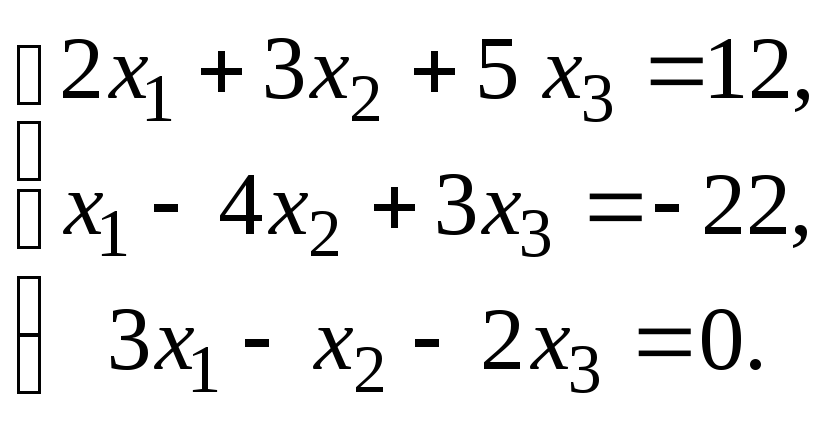 6.
6.

7.
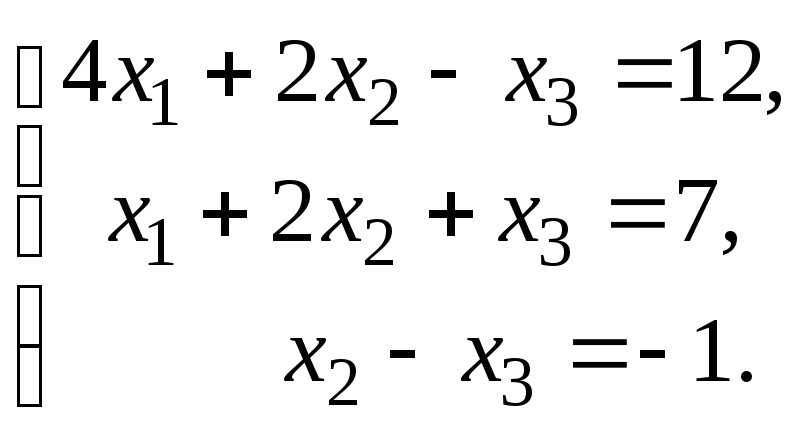 8.
8.
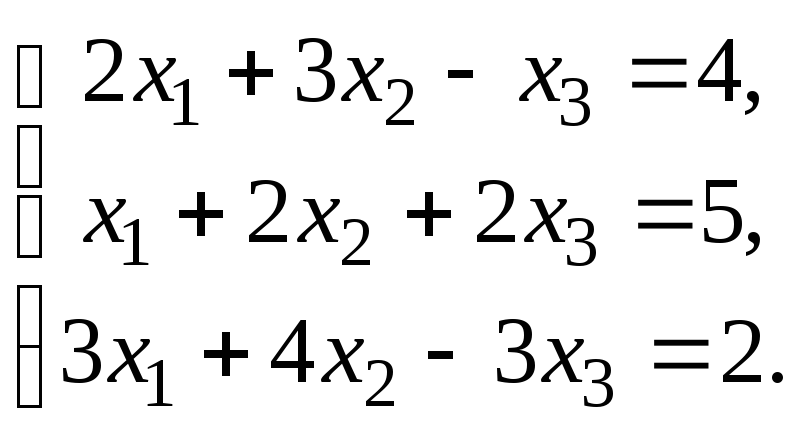
9.
 10.
10.
11. 12.
12.
13. 14.
14.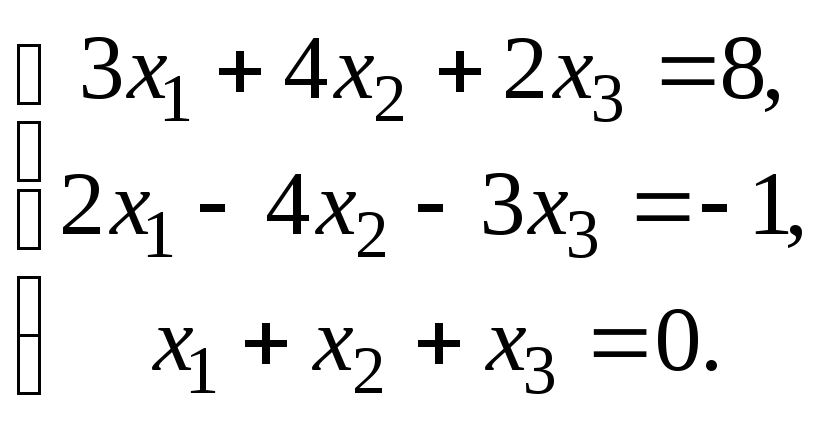
15. 16.
16.
17. 18.
18.
19. 20.
20.
21 – 40. Даны вершины треугольника А, В, С. Найти уравнение и длину высоты, опущенной из вершины В.
21.
![]() 22.
22.
![]()
23.
![]() 24.
24.
![]()
25.
![]() 26.
26.
![]()
27.
![]() 28.
28.
![]()
29.
![]() 30.
30.
![]()
31.
![]() 32.
32.
![]()
33.
![]() 34.
34.
![]()
35.
![]() 36.
36.
![]()
37.
![]() 38.
38.
![]()
39.
![]() 40.
40.
![]()
41 – 60. Найти угол
(в градусах) между плоскостью
![]() и плоскостью, проходящей через точки
М1,
М2,
М3.
и плоскостью, проходящей через точки
М1,
М2,
М3.
41.
![]()
42.
![]()
43.
![]()
44.
![]()
45.
![]()
46.
![]()
47.
![]()
48.
![]()
49.
![]()
50.
![]()
51.
![]()
52.
![]()
53.
![]()
54.
![]()
55.
![]()
56.
![]()
57.
![]()
58.
![]()
59.
![]()
60.
![]()
61 – 80. Упростить уравнение кривой и изобразить ее на рисунке.
61.
![]()
62.
![]()
63.
![]()
64.
![]()
65.
![]()
66.
![]()
67.
![]()
68.
![]()
69.
![]()
70.
![]()
71.
![]()
72.
![]()
73.
![]()
74.
![]()
75.
![]()
76.
![]()
77.
![]()
78.
![]()
79.
![]()
80.
![]()
81 – 100. Найти пределы функций, не пользуясь правилом Лопиталя.
81. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
82. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
83. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
84. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
85. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
86. а)
![]() ; б)
; б)
![]() ;
;
в)
 ; г)
; г)
![]() .
.
87. а)
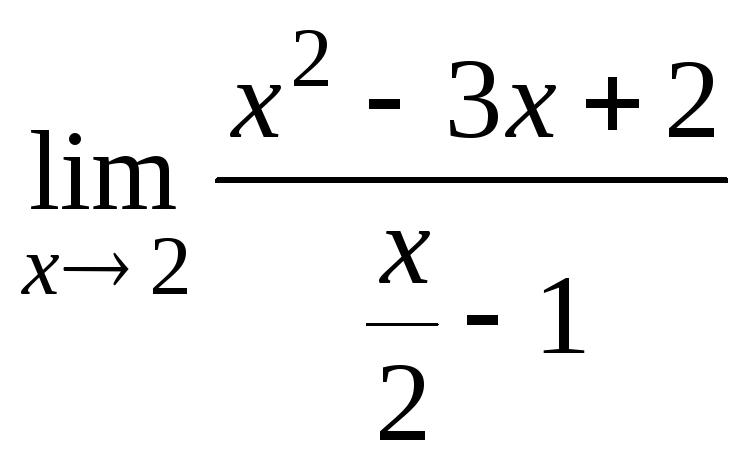 ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
88. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
89. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
90. а)
![]() ; б)
; б)
![]() ;
;
в)
 ; г)
; г)
![]() .
.
91. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
92. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
93. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
94. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
95. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
96. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г).
; г).
![]() .
.
97. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г).
; г).
![]() .
.
98. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г).
; г).
![]() .
.
99. а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г).
; г).
![]() .
.
100. а)
![]() ; б)
; б)
![]() ;
;
в)
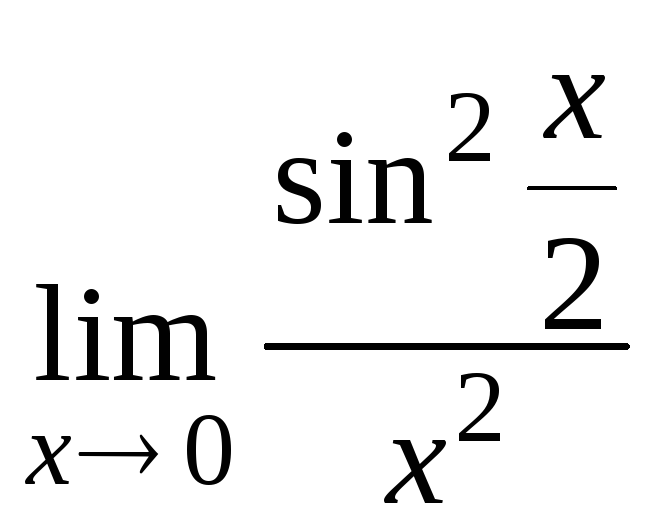 ; г).
; г).
![]() .
.
101 – 120. Исследовать данные функции на непрерывность и указать вид точек разрыва; в условии б дополнительно построить график функции.
101. а)
![]() ;
б)
;
б)

102. а)
![]() ;
б)
;
б)
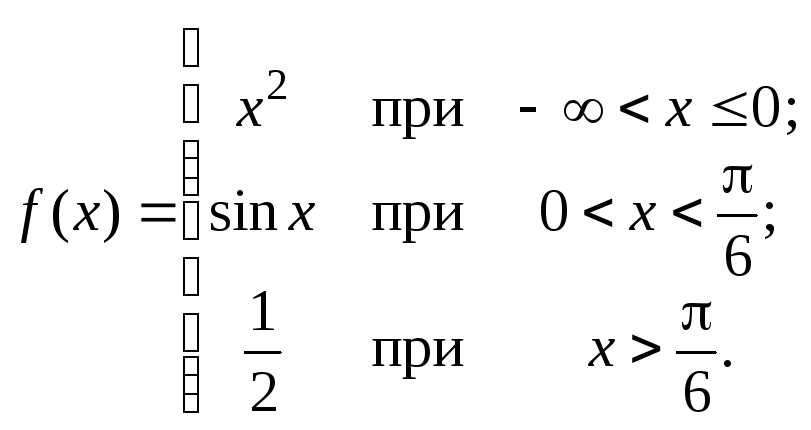
103. а)
![]() ;
б)
;
б)

104. а)
![]() ;
б)
;
б)

105. а)
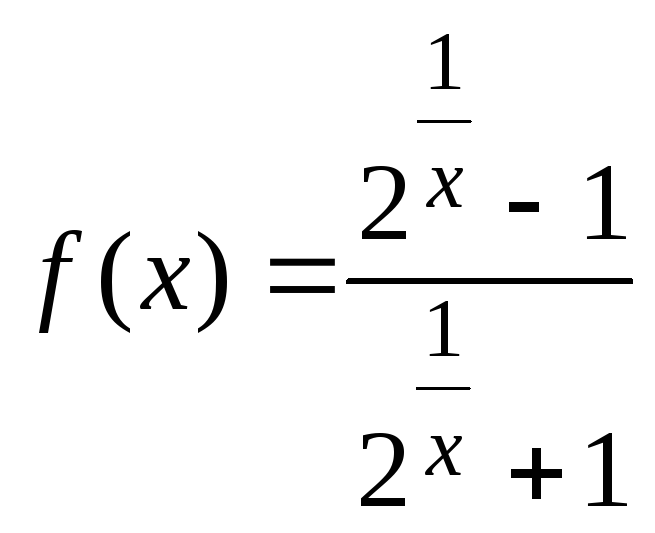 ;
б)
;
б)
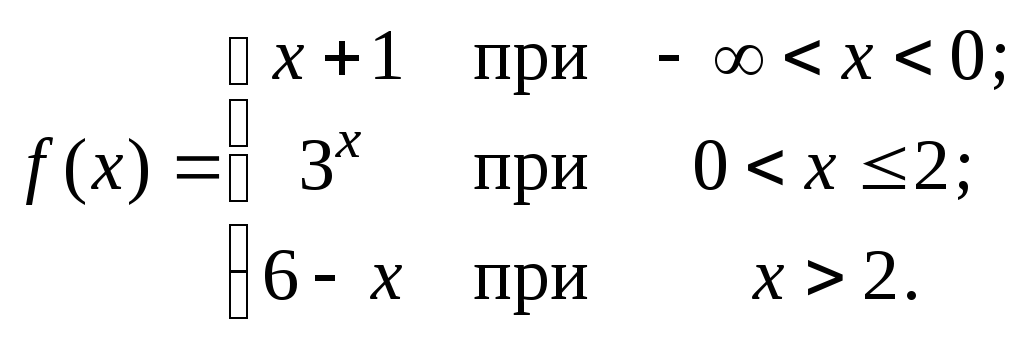
106. а)
![]() ;
б)
;
б)

107. а)
![]() ;
б)
;
б)

108. а)
![]() ;
б)
;
б)
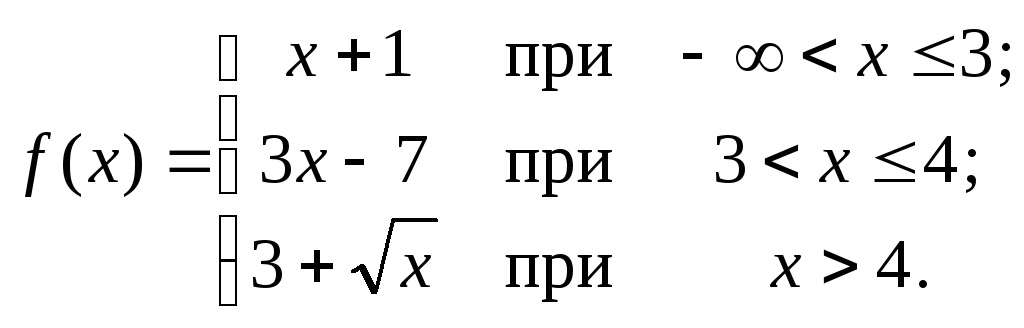
109. а)
![]() ;
б)
;
б)

110. а)
![]() ;
б)
;
б)

111. а)
![]() ;
б)
;
б)

112. а)
![]() ;
б)
;
б)
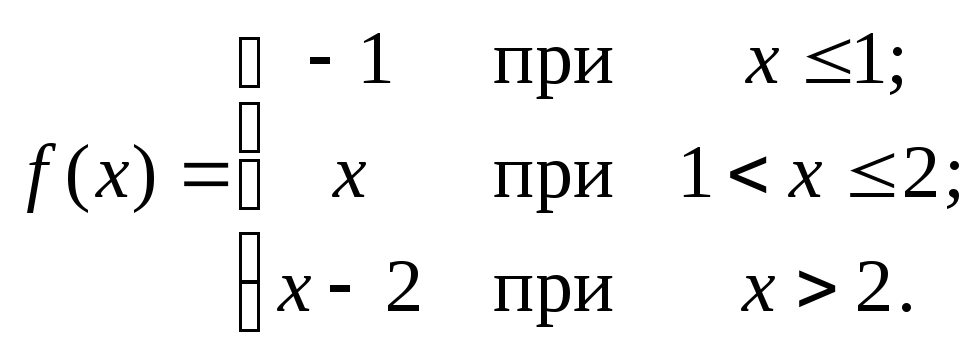
113. а)
![]() ;
б)
;
б)
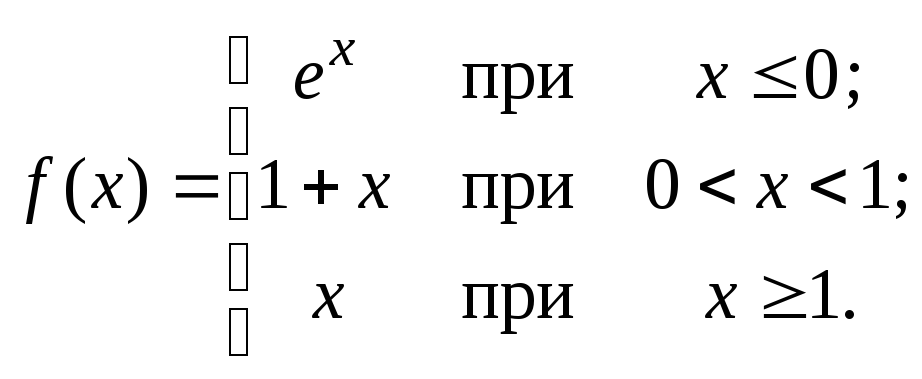
114. а)
![]() ;
б)
;
б)
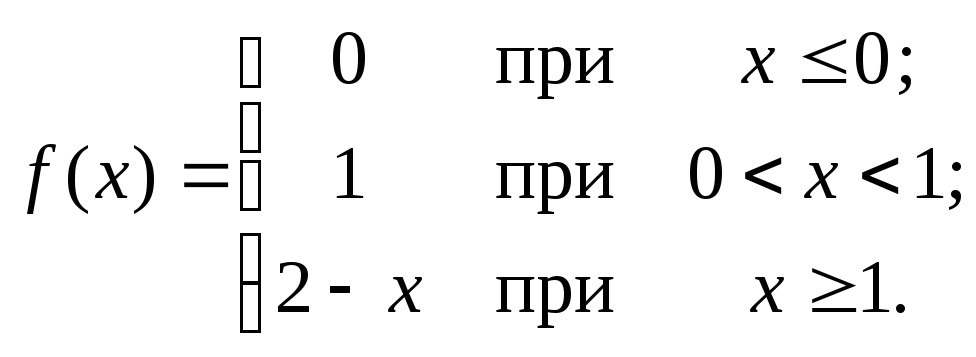
115. а)
![]() ;
б)
;
б)

116. а)
![]() ;
б)
;
б)
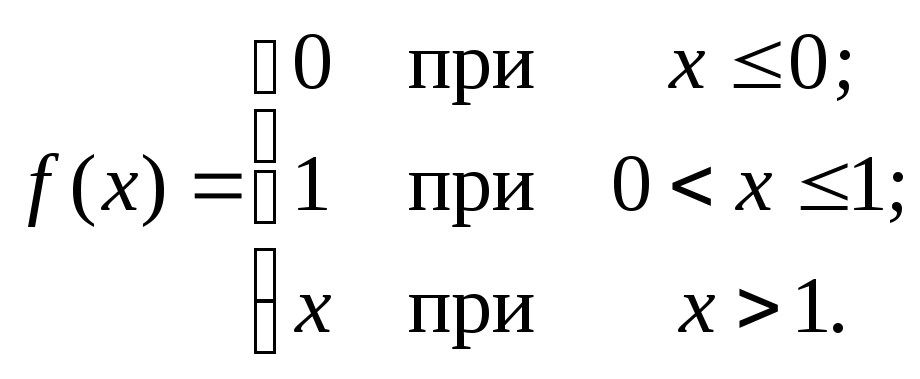
117. а)
![]() ;
б)
;
б)
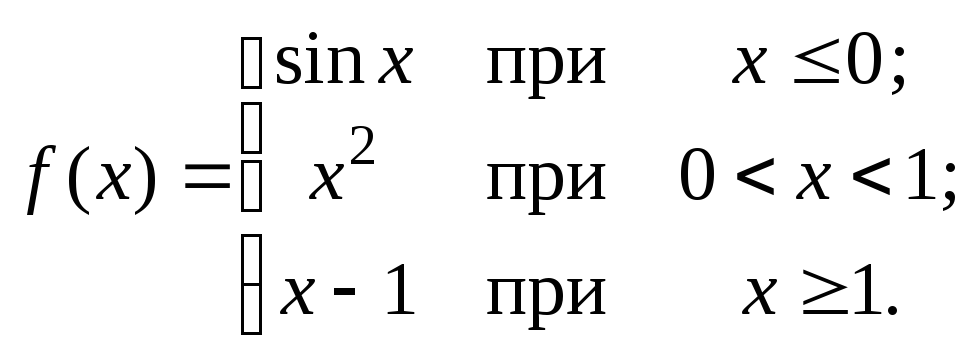
118. а)
![]() ;
б)
;
б)
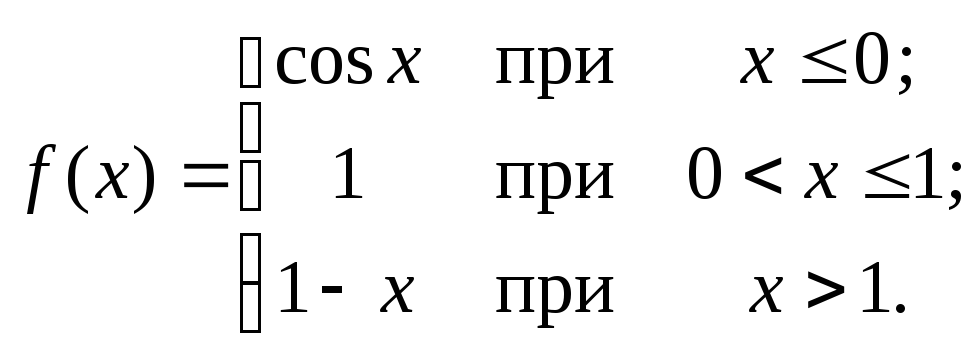
119. а)
![]() ;
б)
;
б)
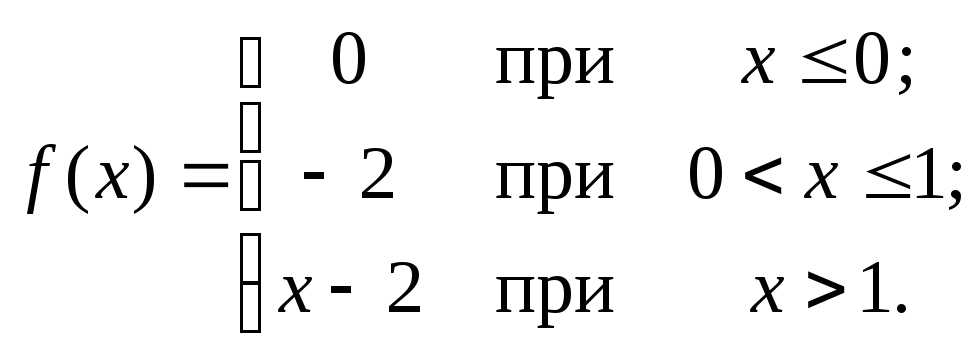
120. а)
![]() ;
б)
;
б)

121 – 140. Найти производные первого и второго порядков от функ-ций, заданных параметрически:
121.
![]()
122.
![]()
123.
![]()
124.
![]()
125.
![]()
126.
![]()
127.
![]()
128.
![]()
129.
![]()
130.
![]()
131.
![]()
132.
![]()
133.
![]()
134.
![]()
135.
![]()
136.
![]()
137.
![]()
138.
![]()
139.
![]()
140.
![]()
141
– 160. Написать формулу Тейлора третьего
порядка с остаточным членом в форме
Лагранжа для заданной функции в точке
![]() .
.
141.
![]() 142.
142.
![]()
143.
![]() 144.
144.
![]()
145.
![]() 146.
146.
![]()
147.
![]() 148.
148.
![]()
149.
![]() 150.
150.
![]()
151.
![]() 152.
152.
![]()
153.
![]() 154.
154.
![]()
155.
![]() 156.
156.
![]()
157.
![]() 158.
158.
![]()
159.
![]() 160.
160.
![]()
161-180. Исследовать функцию и построить ее график.
161.
![]() 162.
162.
![]() 163.
163.
![]()
164.
![]() 165.
165.
![]() 166.
166.
![]()
167.
![]() 168.
168.
![]() 169.
169.
![]()
170.
![]() 171.
171.
![]() 172.
172.
![]()
173.
![]() 174.
174.
![]() 175.
175.
![]()
176.
![]() 177.
177.
![]() 178.
178.
![]()
179.
![]() 180.
180.
![]()
