
лекции / tau_lekciy / 06 - Статические и астатические САР
.docЛекция 6
(4 часа)
СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР
Понятие статических и астатических САР.
Порядок астатизма
Рассмотрим структурную схему САР, изображенную на рис.6.1.
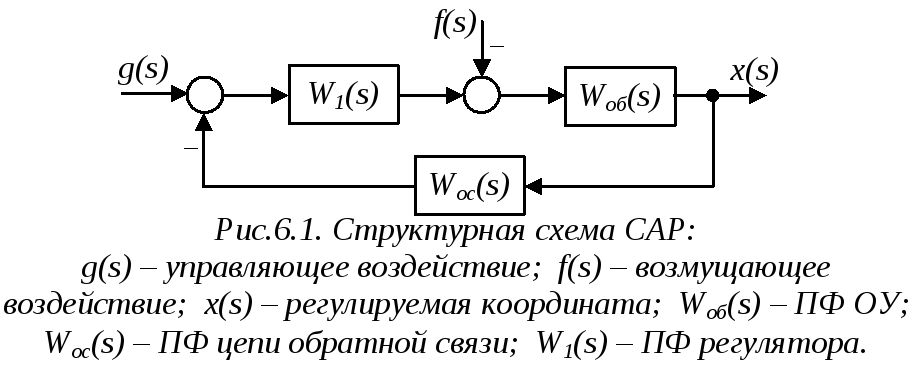
Задача – каким-то образом воспроизводить x(s) в соответствии с заданием g(s), уменьшив при этом (в идеале – исключив) влияние возмущения f(s) на регулируемую координату.
Напоминание. Статической называется система, в которой при наличии возмущения (нагрузки) присутствует ошибка регулирования, зависящая от его величины. В противном случае САР называется астатической. (Лекция 1)
Статизм и астатизм САР рассматривается раздельно применительно к управляющему g(s) и возмущающему f(s) воздействиям.
Для систем точного воспроизведения представляет интерес вопрос, является ли САР статической или астатической по управляющему воздействию. Если ошибка воспроизведения управляющего воздействия
![]()
в установившемся
режиме (при
![]() )
равна нулю, то САР называется астатической
по управляющему воздействию.
В противном случае САР называется
статической.
)
равна нулю, то САР называется астатической
по управляющему воздействию.
В противном случае САР называется
статической.
 Рассмотрим
приведенное определение применительно
к постоянному управляющему воздействию
–
Рассмотрим
приведенное определение применительно
к постоянному управляющему воздействию
–
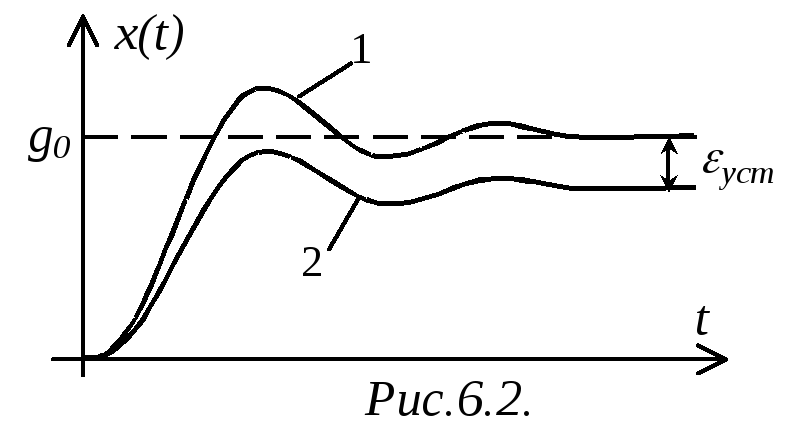
![]() (рис.6.2): в случае 1
(рис.6.2): в случае 1
![]() – следовательно, САР астатическая; в
случае 2
– следовательно, САР астатическая; в
случае 2
![]() отлична от нуля – САР статическая.
отлична от нуля – САР статическая.
Учитывая, что в
системах могут иметь место самые
различные воздействия (см. рис. 4.4 –
типовые воздействия), для астатических
систем вводится понятие порядка
астатизма
![]() (
(![]() 1,
2, 3, …). Так, случаю 1 на рис.6.2 соответствует
порядок астатизма по управляющему
воздействию
1,
2, 3, …). Так, случаю 1 на рис.6.2 соответствует
порядок астатизма по управляющему
воздействию
![]() 1,
случаю 2 –
1,
случаю 2 –
![]() 0
(САР статическая).
0
(САР статическая).
При линейно
изменяющемся управляющем воздействии
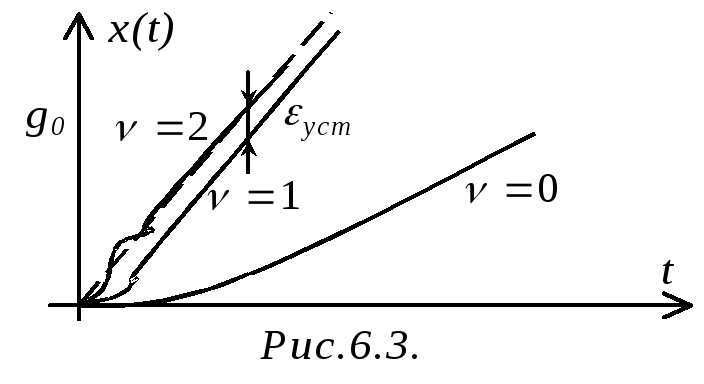
![]() (рис.6.3) (кривая 1-го порядка) ошибка в
установившемся режиме будет равна нулю,
если САР обладает порядком астатизма
(рис.6.3) (кривая 1-го порядка) ошибка в
установившемся режиме будет равна нулю,
если САР обладает порядком астатизма
![]() по управляющему воздействию, при
по управляющему воздействию, при
![]() 1
в установившемся режиме будет иметь
место постоянная ошибка
1
в установившемся режиме будет иметь
место постоянная ошибка
![]() ,
отличная от нуля. При
,
отличная от нуля. При
![]() 0
ошибка будет увеличиваться.
0
ошибка будет увеличиваться.
 Аналогично
вводится понятие астатизма
Аналогично
вводится понятие астатизма
![]() 3
по управляющему воздействию при
квадратичном изменении управления
3
по управляющему воздействию при
квадратичном изменении управления
![]() (рис.6.4) (кривая 2-го порядка) и т.д.
(рис.6.4) (кривая 2-го порядка) и т.д.
Вопросом статизма или астатизма по отношению к возмущающему воздействию интересуются в системах стабилизации. Если возмущающее воздействие оказывает влияние на регулируемую координату в установившемся режиме, то система называется статической по возмущающему воздействию, в противном случае – астатической.
 Под
статической
характеристикой
понимают зависимость
Под
статической
характеристикой
понимают зависимость
![]() при постоянном управляющем воздействии
при постоянном управляющем воздействии
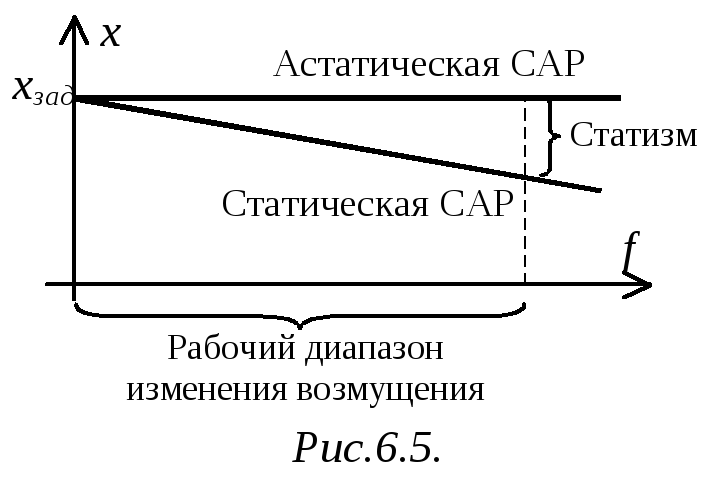
![]() (рис.6.5). Для САР, астатической по
возмущению, статическая характеристика
представляет собой прямую линию,
параллельную оси абсцисс.
(рис.6.5). Для САР, астатической по
возмущению, статическая характеристика
представляет собой прямую линию,
параллельную оси абсцисс.
В технических САР в роли возмущения обычно выступает нагрузка силового агрегата, которая может изменяться в заранее установленном диапазоне (рабочем). При этом максимальное значение возмущения обычно имеет место в нормальном (номинальном) режиме работы САР. Величина ошибка регулируемой координаты в номинальном режиме работы называется статизмом.
Примечание. Одна и та же САР может быть астатической по отношению к управляющему воздействию, но статичной по отношению к возмущающему, и наоборот. Поэтому при использовании терминов статическая или астатическая всегда следует добавлять, по отношению к какому воздействию термин применяется.
Системы точного воспроизведения
Обычно для таких систем ПФ цепи ОС равна единице:
![]() ,
,
т.е., вход равен выходу (рис.6.6).
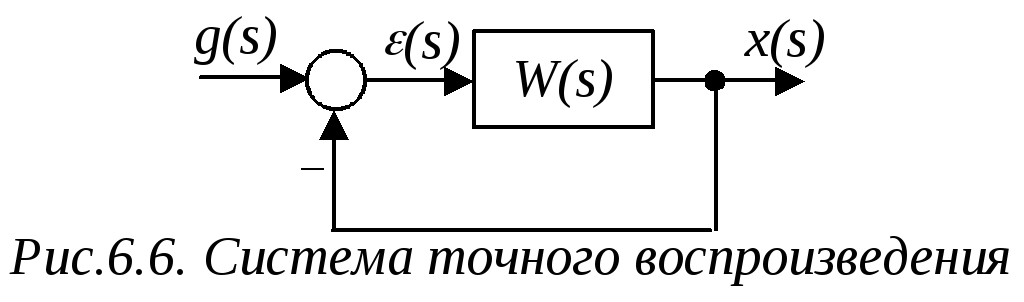 Для
определения установившейся ошибки
может быть использована теорема о
конечном значении (табл.2.2):
Для
определения установившейся ошибки
может быть использована теорема о
конечном значении (табл.2.2):
![]() .
.
Если окажется, что
![]() ,
САР является астатической, в противном
случае – статической.
,
САР является астатической, в противном
случае – статической.
Представим ПФ разомкнутой САР (рис.6.6) в виде:
![]() ,
,
где
![]() – нормированная ПФ разомкнутой САР,
где
– нормированная ПФ разомкнутой САР,
где
![]() .
.
![]() – порядок астатизма
ПФ разомкнутой системы;
– порядок астатизма
ПФ разомкнутой системы;
Система будет
статической (![]() ),
если интегрирующие звенья в чистом виде
отсутствуют, либо все они скомпенсированы
дифференцирующими. В противном случае
САР будет астатической.
),
если интегрирующие звенья в чистом виде
отсутствуют, либо все они скомпенсированы
дифференцирующими. В противном случае
САР будет астатической.
Для определения установившейся ошибки необходимо найти ПФ, считая входом управляющее воздействие g(s), а выходом – сигнал ошибки e(s):
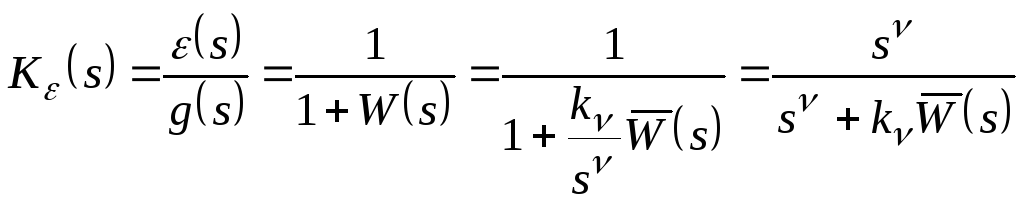 . (1)
. (1)
Тогда установившаяся ошибка может быть вычислена следующим образом:
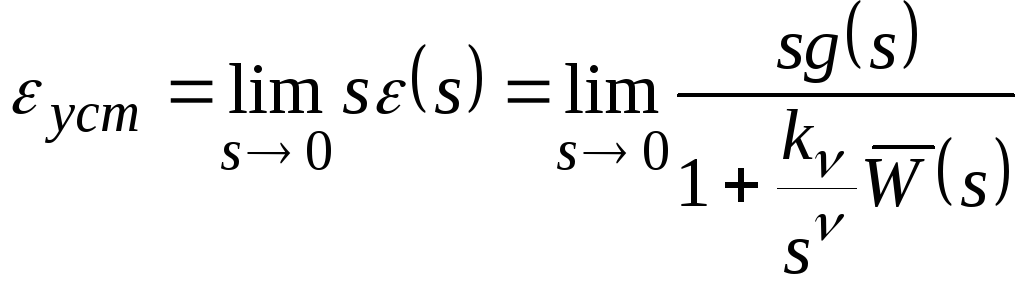 . (2)
. (2)
В частном случае,
при
![]() (постоянное воздействие), когда
(постоянное воздействие), когда
![]() ,
установившаяся ошибка будет равна:
,
установившаяся ошибка будет равна:
![]() . (3)
. (3)
Из (3) видно, что
САР будет астатической, если
![]() .
В противном случае САР будет статической.
Но из (1) следует, что при
.
В противном случае САР будет статической.
Но из (1) следует, что при
![]()
![]() ,
а при
,
а при
![]()
![]() .
.
Таким образом,
если
![]() ,
то САР будет статической, и установившаяся
ошибка будет обратно пропорциональна
коэффициенту усиления
,
то САР будет статической, и установившаяся
ошибка будет обратно пропорциональна
коэффициенту усиления
![]() разомкнутой САР, сложенному с единицей.
разомкнутой САР, сложенному с единицей.
Теоретически ошибку можно приблизить
к нулю, устремляя
![]() к бесконечности. Это положение реализуется
в релейных САР, релейные элементы которых
работают в скользящем режиме.
к бесконечности. Это положение реализуется
в релейных САР, релейные элементы которых
работают в скользящем режиме.
Система будет
астатической, если порядок астатизма
ПФ разомкнутой системы
![]() .
Таким образом, в астатической САР всегда
должны присутствовать интегрирующие
звенья в чистом виде (хотя бы одно) – то
есть, не должны компенсироваться
дифференцирующими звеньями и не должны
быть замкнутыми жесткими ОС.
.
Таким образом, в астатической САР всегда
должны присутствовать интегрирующие
звенья в чистом виде (хотя бы одно) – то
есть, не должны компенсироваться
дифференцирующими звеньями и не должны
быть замкнутыми жесткими ОС.
Обратная связь
является жесткой,
если
![]() ,
если же
,
если же
![]() ,
ОС является гибкой.
,
ОС является гибкой.
Если
![]() ,
то говорят, что замкнутая САР является
астатической 1-го порядка, если
,
то говорят, что замкнутая САР является
астатической 1-го порядка, если
![]() – астатической 2-го порядка и т.д.
– астатической 2-го порядка и т.д.
Таким образом, порядок астатизма замкнутой САР по управляющему воздействию совпадает с порядком астатизма ПФ разомкнутой САР. Это видно из формулы (1).
Доказательство. Пусть имеется САР, ПФ которой по ошибке равна
![]() .
.
Пусть к САР приложено управляющее
воздействие (рис.4.4)
![]() ,
где
,
где
![]() – порядок кривой.
– порядок кривой.
Изображение управляющего воздействия по Лапласу (табл.2.1):
![]() .
.
Вычисляем установившуюся ошибку по (2):
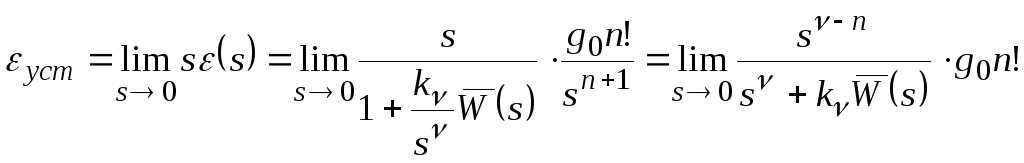
Из последнего выражения следует, что
![]() при
при
![]() .
.
С помощью последней
формулы можно определить установившуюся
ошибку при любых
![]() и
и
![]() .
Так, частные случаи сведены в табл.6.1.
.
Так, частные случаи сведены в табл.6.1.
Табл.6.1.
Установившиеся ошибки
![]()
-
Воздействие
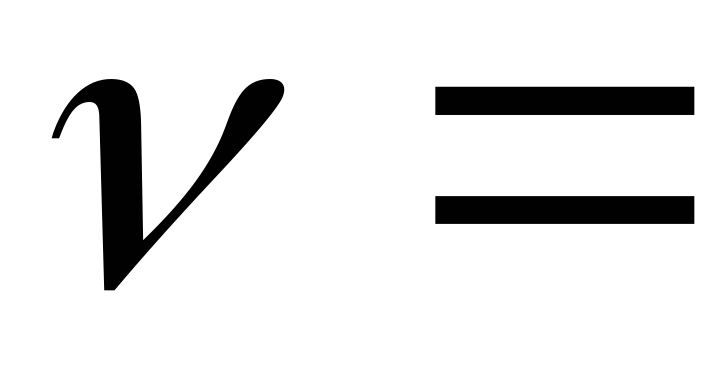 0
0 1
1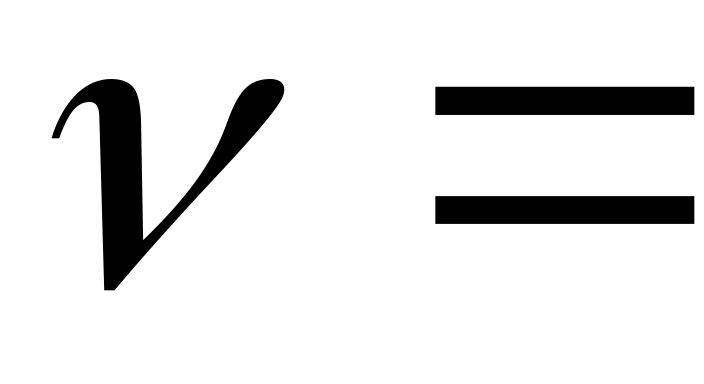 2
2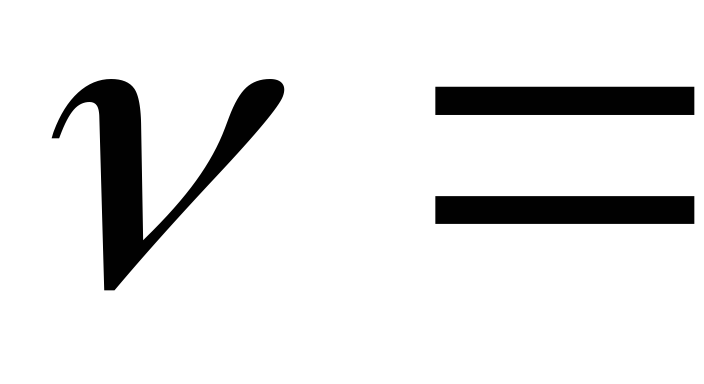 3
3Постоянное (n=0)

0
0
0
Линейное (n=1)

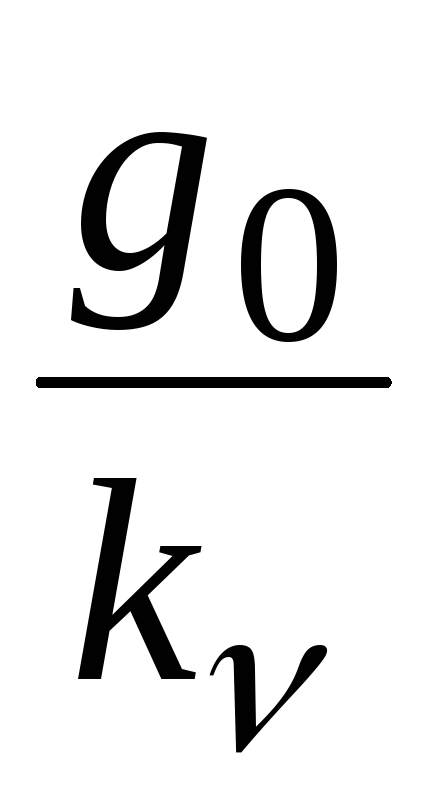
0
0
Парабола (n=2)



0

Таким образом,
астатическая
система 1-го порядка
(![]() )
отрабатывает линейно (n=1)
возрастающий сигнал
)
отрабатывает линейно (n=1)
возрастающий сигнал
![]() – сигнал, изменяющийся с постоянной
скоростью
– сигнал, изменяющийся с постоянной
скоростью
![]() ,
– с ошибкой, прямо пропорциональной
скорости
изменения задающего воздействия V,
и обратно пропорциональной коэффициенту
усиления разомкнутой САР. В установившемся
режиме (рис.6.7) регулируемая координата
x(t)
изменяется также с постоянной скоростью
V.
,
– с ошибкой, прямо пропорциональной
скорости
изменения задающего воздействия V,
и обратно пропорциональной коэффициенту
усиления разомкнутой САР. В установившемся
режиме (рис.6.7) регулируемая координата
x(t)
изменяется также с постоянной скоростью
V.
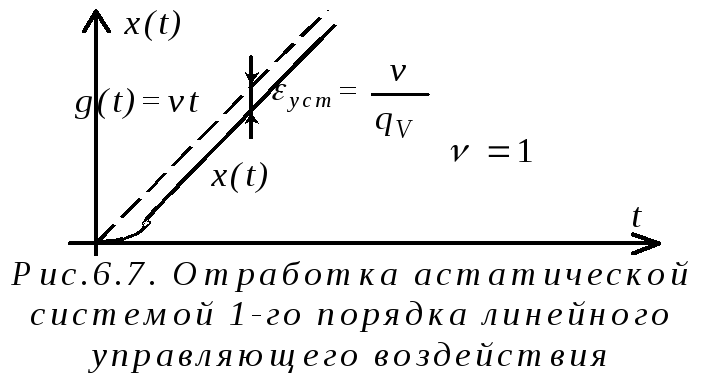 Величина,
показывающая отношение скорости
изменения регулируемой координаты к
ошибке в установившемся режиме, называется
добротностью
САР по скорости,
которая численно равна коэффициенту
усиления
Величина,
показывающая отношение скорости
изменения регулируемой координаты к
ошибке в установившемся режиме, называется
добротностью
САР по скорости,
которая численно равна коэффициенту
усиления
![]() разомкнутой САР:
разомкнутой САР:
![]() .
.
Аналогичным
образом, астатическая
система 2-го порядка
(![]() )
отрабатывает параболически (n=2)
возрастающий сигнал
)
отрабатывает параболически (n=2)
возрастающий сигнал
![]() – сигнал, изменяющийся с постоянным
ускорением
– сигнал, изменяющийся с постоянным
ускорением
![]() ,
– с ошибкой, прямо пропорциональной
ускорению
a,
и обратно пропорциональной коэффициенту
усиления разомкнутой САР. В установившемся
режиме (рис.6.8) регулируемая координата
x(t)
изменяется также с постоянным ускорением
a.
,
– с ошибкой, прямо пропорциональной
ускорению
a,
и обратно пропорциональной коэффициенту
усиления разомкнутой САР. В установившемся
режиме (рис.6.8) регулируемая координата
x(t)
изменяется также с постоянным ускорением
a.
 Величина,
показывающая отношение ускорения
регулируемой координаты к ошибке в
установившемся режиме, называется
добротностью
САР по ускорению,
которая численно равна коэффициенту
усиления
Величина,
показывающая отношение ускорения
регулируемой координаты к ошибке в
установившемся режиме, называется
добротностью
САР по ускорению,
которая численно равна коэффициенту
усиления
![]() разомкнутой САР:
разомкнутой САР:
![]() .
.
Термин добротность системы по скорости применяется к астатическим системам 1-го порядка, а термин добротность системы по ускорению – к астатическим системам второго порядка.
В обоих случаях,
чем выше добротность q,
тем меньше установившаяся ошибка
![]() ,
и тем точнее отработка системой
управляющего воздействия.
,
и тем точнее отработка системой
управляющего воздействия.
Системы стабилизации
Выше уже отмечалось, что для систем стабилизации, помимо астатизма по управлению (как и в системах точного воспроизведения), важным является решение вопроса астатизма САР по возмущающему воздействию. Если возмущающее воздействие влияет на регулируемую координату в установившемся режиме, САР считается статической по возмущению, в противном случае – астатической.
Структурная схема системы стабилизации представлена на рис.6.9.
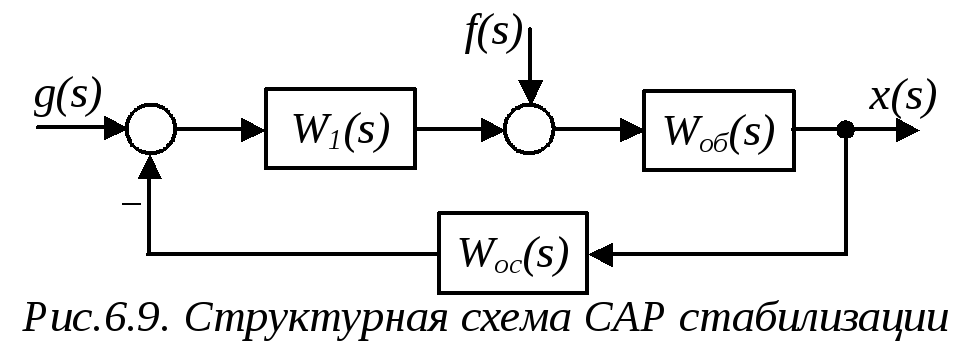 Для
определения влияния возмущения необходимо
сначала найти ПФ САР от возмущения к
выходу. Приравниваем g(s)=0
и, считая цепь со звеньями
Для
определения влияния возмущения необходимо
сначала найти ПФ САР от возмущения к
выходу. Приравниваем g(s)=0
и, считая цепь со звеньями
![]() и
и
![]() отрицательной ОС по отношению к
возмущению, находим:
отрицательной ОС по отношению к
возмущению, находим:
![]() ,
,
где
![]() – ПФ цепи ОС по отношению к возмущающему
воздействию.
– ПФ цепи ОС по отношению к возмущающему
воздействию.
Представим ПФ в знаменателе последнего выражения в виде:
![]()
![]() ,
,
где
![]() – порядок астатизма ПФ ОУ;
– порядок астатизма ПФ ОУ;
![]() – порядок астатизма
ПФ цепи ОС по отношению к возмущающему
воздействию;
– порядок астатизма
ПФ цепи ОС по отношению к возмущающему
воздействию;
![]() ,
,
![]() – соответствующие нормированные ПФ.
– соответствующие нормированные ПФ.
Тогда искомая ПФ
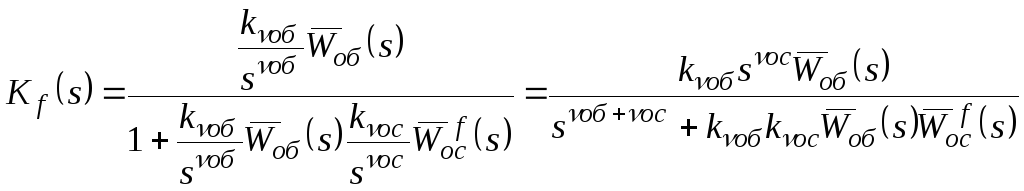 .
.
Для исключения
влияния возмущения на регулируемую
координату (то есть, для обеспечения
астатизма САР по возмущению) необходимо,
чтобы
![]() .
Из последнего выражения следует, что
для этого необходимо, чтобы
.
Из последнего выражения следует, что
для этого необходимо, чтобы
![]() .
.
Астатизм САР по возмущающему воздействию определяется порядком астатизма цепи ОС по отношению к возмущению и не зависит от порядка астатизма ОУ. Другими словами, если чистые интеграторы отсутствуют в цепи ОС, то система будет статической, независимо от того, есть ли интеграторы в ОУ или нет.
Пример 1. Определить, является ли система (рис.6.10) астатической по управляющему и возмущающему воздействиям?
Решение. Находим ПФ разомкнутой САР:
![]() .
.
Таким образом,
![]() ,
следовательно, по отношению к управляющему
воздействию система астатическая 1-го
порядка.
,
следовательно, по отношению к управляющему
воздействию система астатическая 1-го
порядка.
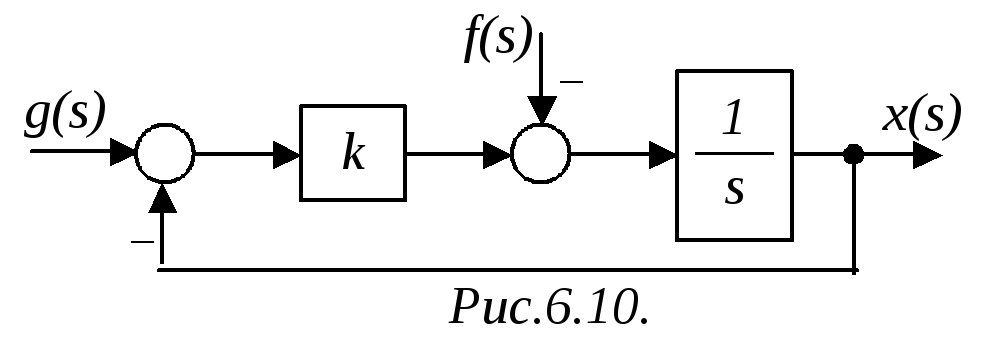 Находим
ПФ цепи отрицательной ОС по отношению
к возмущению:
Находим
ПФ цепи отрицательной ОС по отношению
к возмущению:
![]() .
.
Таким образом,
![]() ,
следовательно, система является
статической по отношению к возмущающему
воздействию.
,
следовательно, система является
статической по отношению к возмущающему
воздействию.
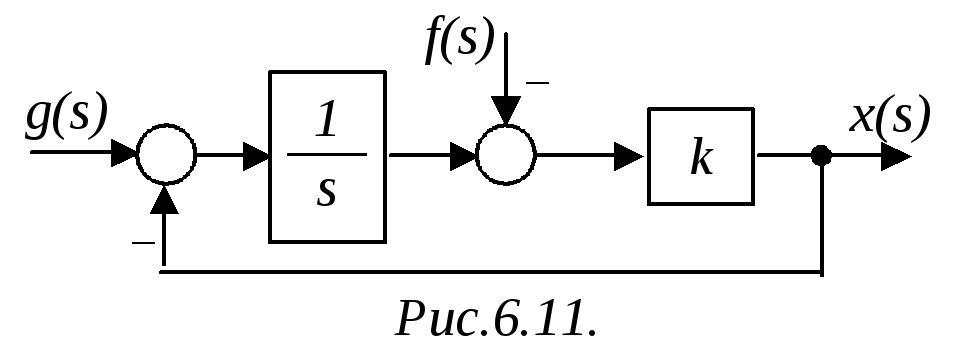
Пример 2. Определить, является ли система (рис.6.11) астатической по управляющему и возмущающему воздействиям?
Решение. Находим ПФ разомкнутой САР:
![]() .
.
Таким образом,
![]() ,
следовательно, по отношению к управляющему
воздействию система астатическая 1-го
порядка.
,
следовательно, по отношению к управляющему
воздействию система астатическая 1-го
порядка.
 Находим
ПФ цепи отрицательной ОС по отношению
к возмущению:
Находим
ПФ цепи отрицательной ОС по отношению
к возмущению:
![]() .
.
Таким образом,
![]() ,
следовательно, и по отношению к
возмущающему воздействию система
является астатической 1-го порядка.
,
следовательно, и по отношению к
возмущающему воздействию система
является астатической 1-го порядка.
Уравнения и передаточные функции системы
"силовой преобразователь – двигатель"
Принципиальная схема система "преобразователь – двигатель" представлена на рис.6.12а.
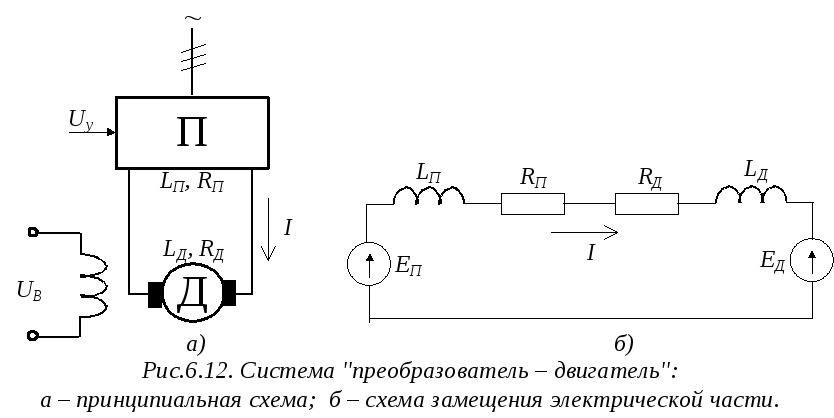
Тиристорный преобразователь П предназначен для выпрямления сетевого трехфазного напряжения, на его выходе имеем выпрямленное ЭДС преобразователя EП, величина которого зависит от значения напряжения управления Uy. Электромагнитные свойства преобразователя характеризуются активным сопротивлением RП и индуктивностью LП.
ЭДС, наводимая в обмотке якоря двигателя EД направлена встречно с ЭДС преобразователя EП и пропорциональна частоте вращения вала двигателя. Индуктивность и активное сопротивление цепи якоря двигателя Д
![]() ;
; ![]() ,
,
где
![]() ,
,
![]() – параметры цепи собственно якоря
двигателя;
– параметры цепи собственно якоря
двигателя;
![]() ,
,
![]() – параметры обмотки добавочных полюсов;
– параметры обмотки добавочных полюсов;
![]() ,
,
![]() – параметры компенсационной обмотке.
– параметры компенсационной обмотке.
Электрическая схема замещения электрической части системы "преобразователь – двигатель" представлена на рис.6.12б.
Обозначив
![]() ;
;
![]() ,
,
дифференциальное уравнение электрического равновесия цепи якоря запишем в следующем виде:
![]() .
.
Соответствующее уравнение в изображениях Лапласа:
![]() .
.
Обозначим
![]() – электромагнитная постоянная времени
силовой цепи якоря двигателя, с. Тогда
последнее уравнение запишется в виде:
– электромагнитная постоянная времени
силовой цепи якоря двигателя, с. Тогда
последнее уравнение запишется в виде:
![]() ,
,
откуда
![]() . (1)
. (1)
ЭДС двигателя пропорциональна частоте вращения вала:
![]() ,
,
или, переходя к изображениям Лапласа,
![]() , (2)
, (2)
где
![]() – конструктивная постоянная,
пропорциональная номинальному магнитному
потоку двигателя.
– конструктивная постоянная,
пропорциональная номинальному магнитному
потоку двигателя.
Наконец, уравнение механического равновесия
![]() ,
,
где M – электромагнитный момент, развиваемый двигателем; MC – момент статического сопротивления (нагрузки); J – суммарный момент инерции вала двигателя.
Уравнение электромагнитного момента имеет вид:
![]() ,
,
и формально статический момент может быть представлен в аналогичном виде:
![]() ,
,
где
![]() – ток статической нагрузки.
– ток статической нагрузки.
С учетом этого уравнение механического равновесия может быть представлено в виде:
![]() .
.
Переходя к изображениям Лапласа:
![]() ,
,
после преобразований получим:
![]() .
.
Вводя понятие
электромеханической постоянной времени
![]() ,
последнее уравнение представим в
окончательном виде:
,
последнее уравнение представим в
окончательном виде:
![]() . (3)
. (3)
Уравнениям (1) – (3) соответствует структурная схема, представленная на рис.6.13.
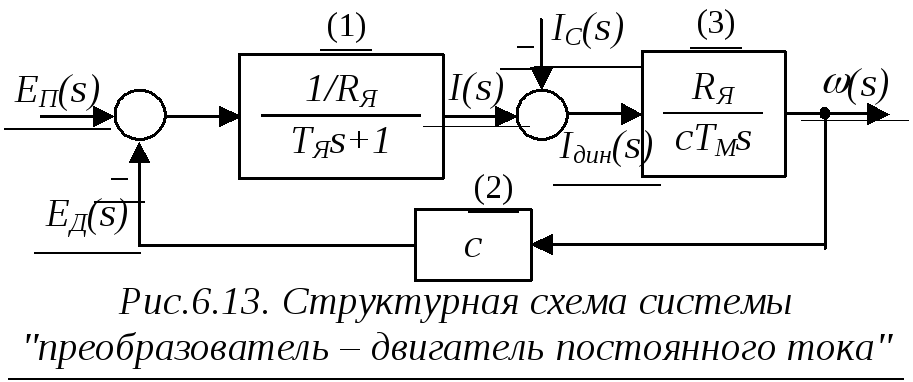
Анализируя структурную схему (рис.6.13), можно увидеть, что данная система астатическая по отношению к управляющему воздействию EП(s) (поскольку присутствует чистый интегратор в блоке (3)), и в то же время статическая по отношению к возмущающему воздействию IC(s) (в блоках (1) и (2) отсутствуют интеграторы). Таким образом, при изменении нагрузки IC на валу двигателя будет изменяться и скорость (s).
ПФ по управляющему воздействию:
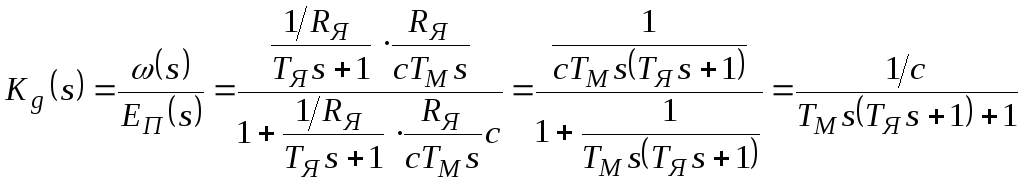 .
.
В установившемся режиме
![]() , и
, и ![]() .
.
ПФ по возмущающему воздействию:
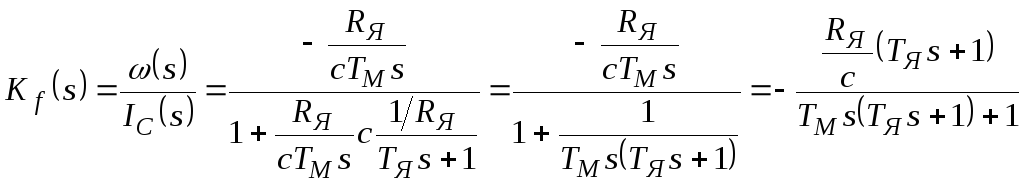 .
.
Установившаяся ошибка:
![]() .
.
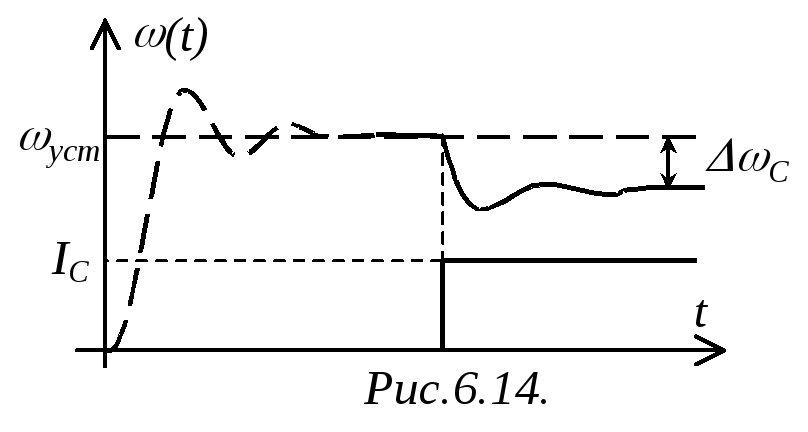 Т.е.,
при подаче какого-то управляющего
воздействия (рис.6.14) двигатель каким-то
образом (показано пунктирной линией)
разгонится до скорости
Т.е.,
при подаче какого-то управляющего
воздействия (рис.6.14) двигатель каким-то
образом (показано пунктирной линией)
разгонится до скорости
![]() .
После скачкообразного приложения
возмущающего воздействия (наброса
нагрузки) будет иметь место ошибка
регулирования, которая после затухания
переходного процесса будет равна
.
После скачкообразного приложения
возмущающего воздействия (наброса
нагрузки) будет иметь место ошибка
регулирования, которая после затухания
переходного процесса будет равна
![]() .
.
Сравнивая ПФ
![]() и
и
![]() ,
видим, что знаменатели, т.е., характеристические
полиномы двигателя, остаются одинаковыми
вне зависимости от того, что является
входом, и что – выходом.
,
видим, что знаменатели, т.е., характеристические
полиномы двигателя, остаются одинаковыми
вне зависимости от того, что является
входом, и что – выходом.
Этот вывод можно
распространить на любую замкнутую САР:
характеристический полином
![]() не зависит от того, на основании какой
ПФ он записан.
не зависит от того, на основании какой
ПФ он записан.
Для определения
характера переходного процесса при
подаче управляющего воздействия
рассмотрим детальней ПФ
![]() :
:
![]() .
.
Таким образом,
если
![]() ,
будем иметь колебательное звено, если
же
,
будем иметь колебательное звено, если
же
![]() ,
то данная ПФ является ПФ двух последовательно
соединенных апериодических звеньев.
,
то данная ПФ является ПФ двух последовательно
соединенных апериодических звеньев.
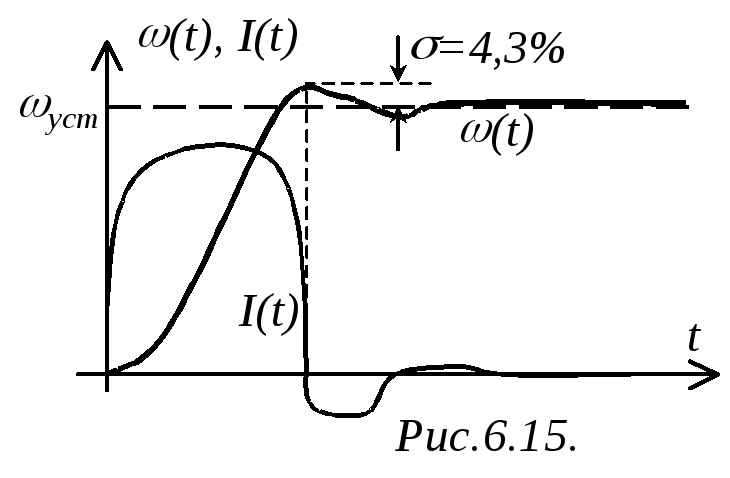 Например,
при
Например,
при
![]() и
и
![]() переходный процесс по току и скорости
качественно будет иметь вид, показанный
на рис.6.15. Отметим, что точки экстремума
кривой (t)
совпадают по времени с нулевыми значениями
I(t),
поскольку ток, согласно (3), является
производной от скорости.
переходный процесс по току и скорости
качественно будет иметь вид, показанный
на рис.6.15. Отметим, что точки экстремума
кривой (t)
совпадают по времени с нулевыми значениями
I(t),
поскольку ток, согласно (3), является
производной от скорости.
