;

;

; ;

преобразование :

 

; ;

 

;

 

 

; ;

 

 

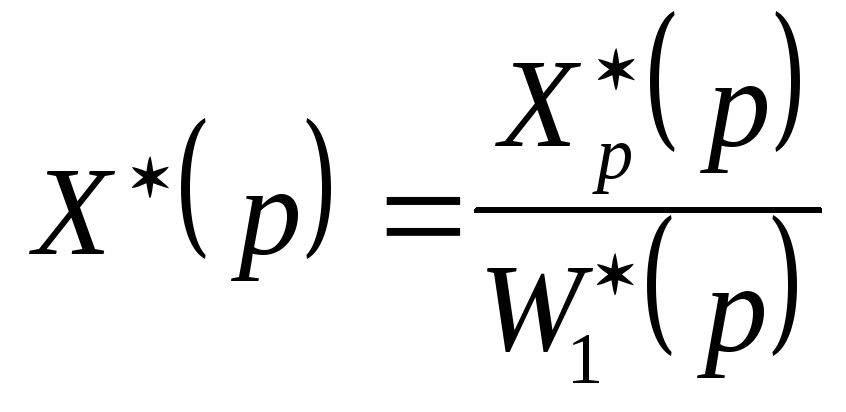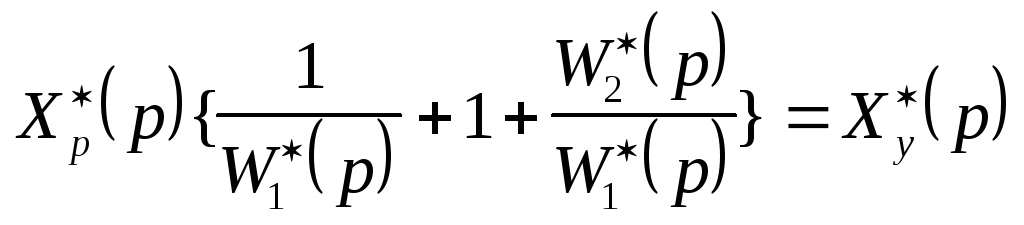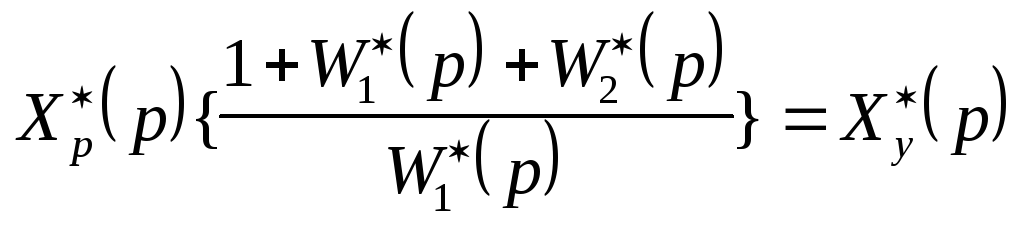2-ой способ :

;

Правила структурного преобразования импульсных систем :

В непрерывной части импульсной системе можно производить любые преобразования .

Нельзя переставлять передаточную функцию и импульсный элемент .

Когда импульсный элемент стоит на входе системы , можно написать передаточную функцию непрерывной замкнутой системы , а затем проставить звездочки .

 

 

 

52 . Устойчивость импульсных систем . Необходимые и достаточные условия устойчивости .

Система устойчива , если после снятия кратковременного воздействия она возвращается в исходное состояние .

 

 

 

 

 

Если непрерывная система устойчива , то импульсная система будет также устойчива .

 

 

 

 

 

 

 

Необходимое и достаточное условие устойчивости импульсных систем .

 

-корни ; ;

 

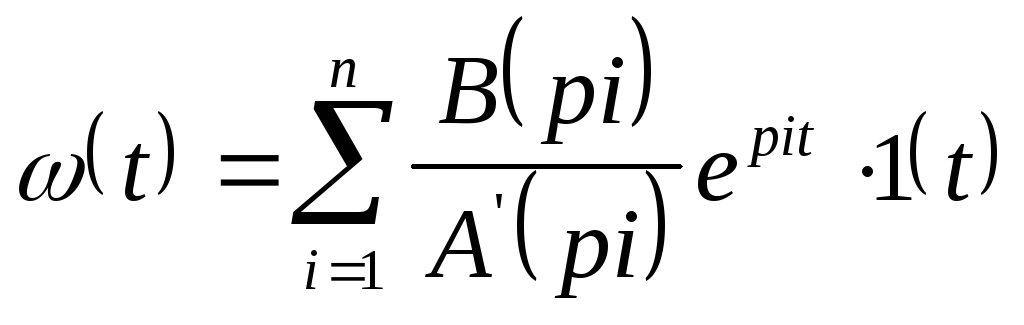- форма разложения .

 

; ;

 

; ; ( ) ; ;

 

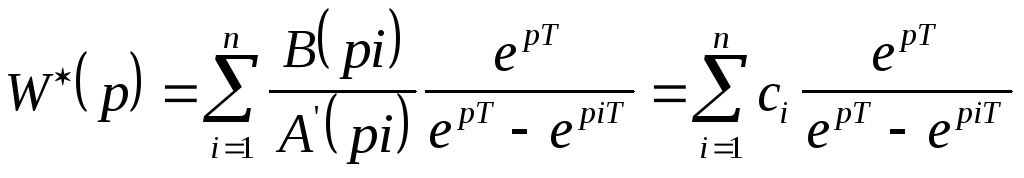; ; ; ( корни , ) .

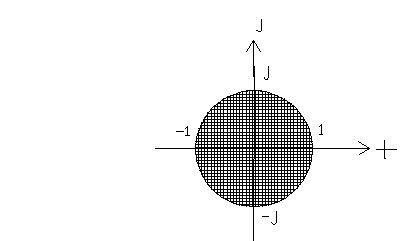
	1)    В полосе ; полюса дискретной передаточной функции и непрерывной передаточной функции совпадают . 2)    Если непрерывная передаточная функция устойчива , то соответствующая ей дискретная передаточная функция устойчива . Для устойчивости импульсной системы необходимо и достаточно , чтобы полюса ее дискретной передаточной функции лежали в левой части комплексной плоскости . Система нейтральна , если хотя бы один из них попадает на ось .
Система неустойчива , если хотя бы один попадает в правую часть плоскости .

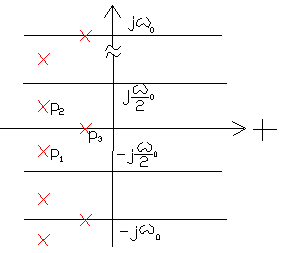
53 . Критерий Гурвица для импульсных систем .

- упреждение на 1 такт квант.

-запаздывание на 1 такт квант .

P	0	-1
Z	1

 

Для устойчивости системы необходимо и достаточно , чтобы полюса характеристического полинома А*(Z) лежали внутри окружности единичного радиуса . Система нейтральна , если хотя бы один полюс попадает на окружность единичного радиуса . Система неустойчива , если хотя бы один полюс попадает вне окружности единичного радиуса .

 

 

Применение критерия Гурвица к анализу устойчивости импульсных систем .

;

; ;

; ; ;

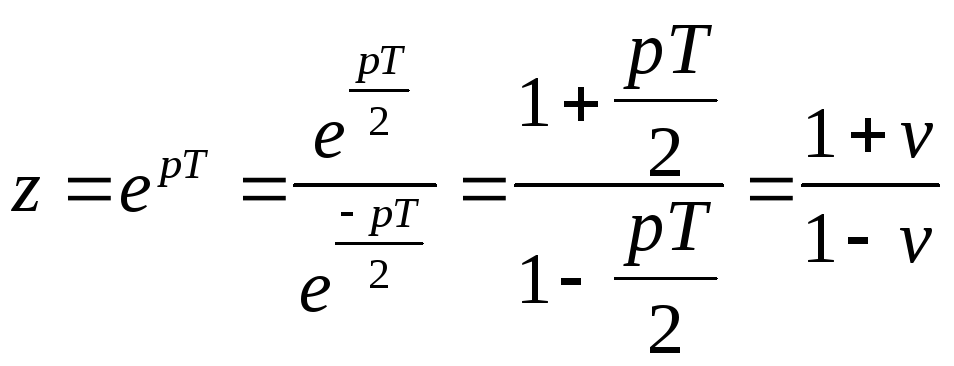Z	1	-1	j	-j	0
V	0	¥	j	-j

 

 

 

54 . Критерий устойчивости Найквиста для импульсных систем .

Критерий устойчивости Найквиста так же как и для непрерывных систем позволяет судить об устойчивости замкнутой импульсной системы по амплитудно-частотной характеристике (АЧХ), или годографу Найквиста, разомкнутой импульсной системы. При этом АЧХ может быть построена экспериментально.

По аналогии с критерием для непрерывных систем сформируем функцию.

С учетом равенства ,

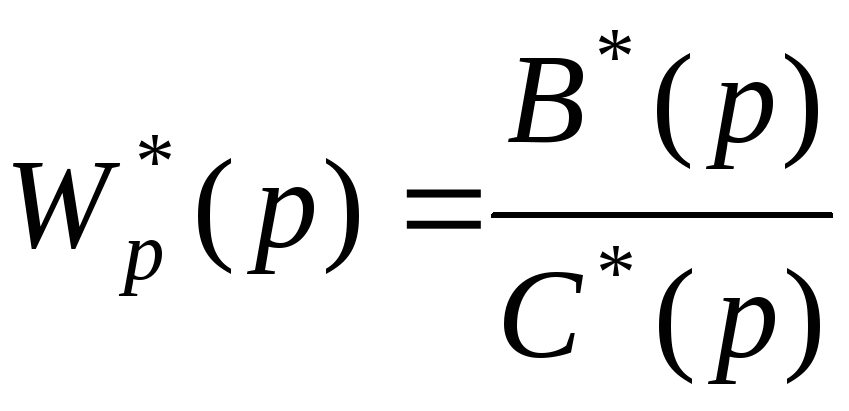где - полиномы от степени m и n соответственно (mn) ,

 

можно записать

.

Таким образом, функция связывает характеристический полином замкнутой импульсной системы с характеристическим полиномом разомкнутой системы .

Так же как и для случая непрерывных систем, найдем приращение аргумента вектора при изменении частоты в диапазоне : .

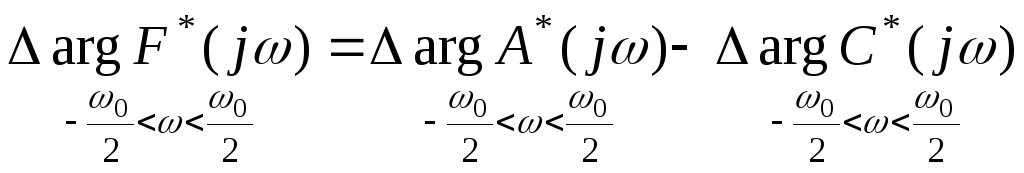или в диапазоне : .

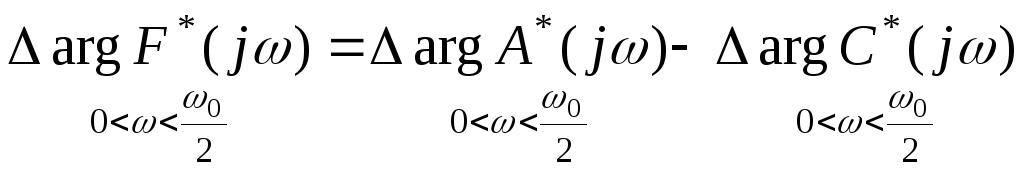Поскольку мы интересуемся условиями устойчивости замкнутой системы, при выполнении которых все n корней характеристического полинома лежат внутри окружности единичного радиуса, то в соответствии с принципом аргумента для импульсных систем

.

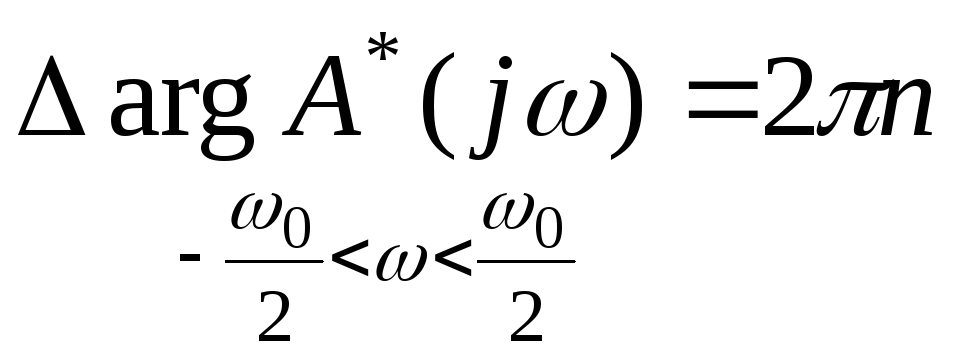
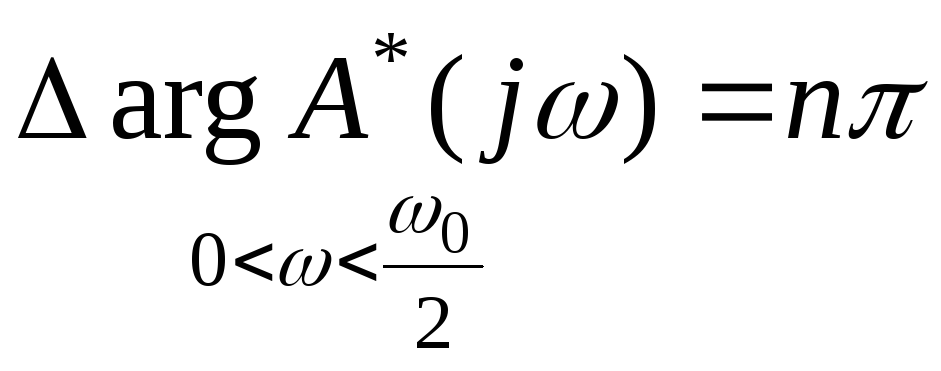Для определения приращения аргумента вектора рассмотрим три случая:

1. a)      Разомкнутая импульсная система устойчива, т.е. все n корней ее характеристического полинома лежат внутри окружности единичного радиуса. Тогда в соответствии с принципом аргумента

и

а приращение аргумента функции будет равно нулю в соответствии с выражениями

и

.

Рассмотрим геометрическую интерпретацию этой ситуации.

На рис.1.11 а представлен график функции , для которой изменение аргумента при изменении частоты в диапазоне равно нулю, а на рис. 1.11 б - график соответствующей ей .

 

 

а б

Рис.1.11