3.2. Амплитудно-частотная характеристика систем.

При анализе процессов преобразования сигналов электрическими цепями представляет интерес исследование зависимостей пере­даточных и входных функций рассматриваемой цепи от часто­ты. График частотной зависимости модуля передаточной функ­ции называется амплитудно-частотной характеристикой, а гра­фик зависимости аргумента передаточной функции от частоты – фазочастотной характеристикой. Обе зависимости, построенные в широком частотном диапазоне, дают наглядное представление о характере передачи сигналов данной цепью.

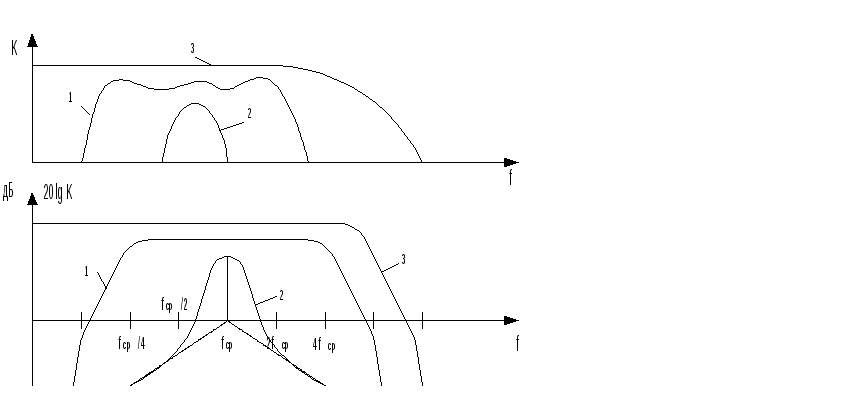
Рисунок 3.2

На Рис. 3.7 приведены частотные характеристики уси­лителя, различающиеся между собой по диапазону пропускаемых частот. Характеристика 1 соответствует широкополосному усили­телю, у которого частотный диапазон сигналов, усиливаемых с оди­наковым коэффициентом усиления K­_ср может быть довольно значи­телен. Характеристика 2 относится к избиратель­ному усилителю, усиливающему сигналы в узкой полосе частот. У некоторых типов усилителей АЧХ (кривая 3) может не иметь завала в области низких частот, у них K_f->0 = K_f->fср. Такие усилители, предназначенные для работы при весьма низких частотах и на постоянном токе, носят название усилителей постоянного тока.

Изменение коэффициента усиления в функции частоты позволяет говорить о частотных искажениях, которые называются линейными, так как не сопровождаются искажением формы усиливаемого сиг­нала, если входной сигнал гармонический. АЧХ и ФЧХ всегда снимаются при такой амплитуде входного сигнала, при какой можно не опасаться нелинейных искажений формы выходного сиг­нала в процессе усиления.

Для количественной оценки частотных искажений пользуются понятием коэффициента частотных искажений М, который пред­ставляет собой отношение коэффициента усиления на средней ча­стоте Kср к коэффициенту усиления на данной частоте. Обычно рас­сматривают частотные искажения, возникающие на границах диапазона f_ниж и f_верх. Соответственно этому определяют коэффициенты частотных искажений

M_н = K_ср/K_н и M_в = K_ср/K_в

Частотные искажения сопровождаются сдвигом фазы между входным и выходным сигналом, или, иначе говоря, фазовыми искаже­ниями.

Разность частот f_в – f_н называют рабочим диапазоном частот устройства (полосой пропускания). Как следует из определения коэффициента частотных искажений, полоса пропускания является субъективной характеристикой и всегда требуется уточнение, по какому уровню сигнала она отсчитывается. Наиболее часто границы полосы пропускания определяют по уменьшению выходной мощности сигнала в два раза, что соответствует уменьшению напряжения (тока) в раз.

Амплитудные и фазовые характеристики часто изображают не в линейном, а в логарифмическом масштабе (рис. 4.7,б), когда на оси ординат амплитудно-частотной характеристики указывают не сам модуль передаточной функции, а его логарифм. На логарифмических частотных характеристиках принято откладывать значение 20lgК. Эта величина оценивается в децибелах. При этом значению модуля К = 10 отвечает значение рассматриваемой функции в 20 дБ.

Положительные значения 20lgК отвечают усилению сигна­ла данной цепью, отрицательные — его ослаблению. Заметим, что фазовый сдвиг j на фазочастотных характеристиках откла­дывают в линейном масштабе.

При построении графика логарифмической АЧХ (ЛАЧХ) LKu = 20lgKu no оси абсцисс удобно откладывать значения частоты через октаву. Октава равна разности частот 2f и f. Если использовать логарифмическую шкалу с основанием логарифма 2, то расстояние между соседними отсчётами будет равно log₂2f — log₂ f = 1.

Если диапазон частот, отражаемый на графике, приближается к 10⁵—10⁶ Гц, целесообразно применить более крупную единицу — декаду, которая соответствует интервалу частот между 10f и f, т. е. lg10f – lgf = 1. Логарифмический масштаб позволяет одинаково подробно изображать на графике область как низких, так и верх­них частот.

За единицу по оси ординат принят децибел. На рис. 4.7,б приведены в логарифмическом масштабе графики кривых, изобра­женных на рис. 4.7, а. Кривые имеют в каждой частотной области определенный наклон. Его выражают в изменении коэффициента усиления, происходящем за одну октаву (декаду). Наклон ±6 дБ/окт (±20 дБ/дек) имеют ЛАЧХ соответственно дифференцирующих и интегрирующих RC-цепей.