
- •Устойчивость систем автоматического управления.
- •Основные понятия теории устойчивости.
- •Алгебраические критерии устойчивости.
- •Необходимое условие устойчивости.
- •Критерий устойчивости Гурвица.
- •3.3.3. Критерий устойчивости Рауса.
- •Частотные критерии устойчивости
- •Принцип аргумента.
- •Критерий устойчивости Найквиста.
- •Запасы устойчивости.
- •Оценка устойчивости по лчх
- •3.5. Выделение областей устойчивости
- •Допустим, что коэффициенты характеристического уравнения
3.5. Выделение областей устойчивости
Среди физических параметров, характеризующих САУ, всегда имеется несколько, легко поддающихся изменению и использующихся для определенной настройки системы. При конструировании системы весьма важно знать диапазоны значений изменяемых параметров, допустимые с точки зрения сохранения устойчивости САУ. Об этих диапазонах можно судить, если в пространстве изменяемых параметров построить область устойчивости, т.е. выделить область значений параметров, при которых система сохраняет устойчивость.
Область устойчивости в теории автоматического управления принято называть D – областью, а представление области параметров в виде областей устойчивости и неустойчивости называют D – разбиением.
3.5.1. Построение области устойчивости по алгебраическим критериям
Допустим, что коэффициенты характеристического уравнения
![]()
зависят от двух изменяемых параметров и . Для построения области устойчивости прежде всего нужно, в соответствии с необходимым условием устойчивости, выделить область изменяемых параметров при нахождении в которой, коэффициенты характеристического уравнения положительны. Это можно сделать, решив систему уравнений
![]() (3.26)
(3.26)
![]()
Для построения границы положительности коэффициентов аi необходимо из решений уравнений (3.26) выбрать те, которые обеспечивают положительность всех коэффициентов. Из всех границ положительности только две одновременно могут быть и границами устойчивости. Такими являются границы, уравнениями которых являются
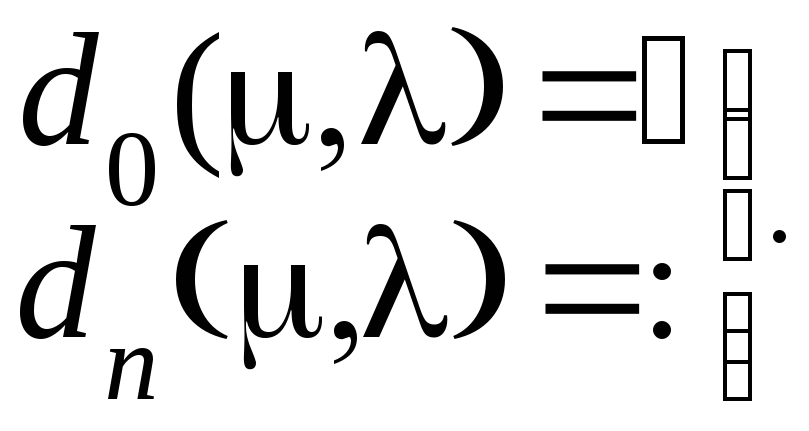 (3.27)
(3.27)
Доказано, что если d0 и dn приблизятся к нулю, то характеристическое уравнение будет иметь два действительных корня
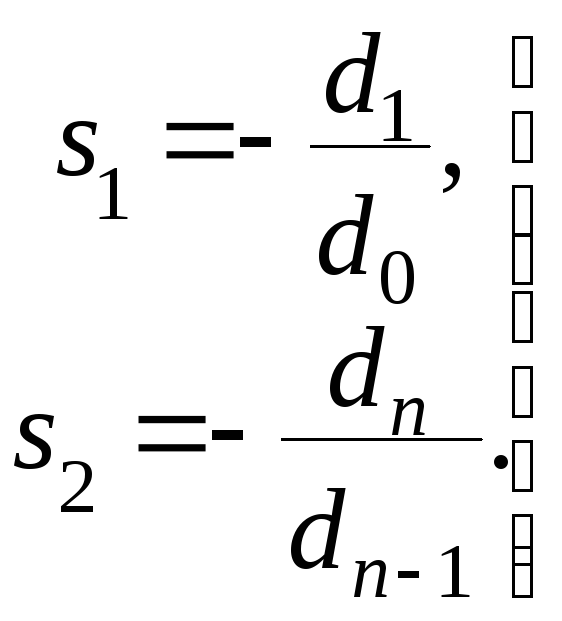 (3.28)
(3.28)
При дальнейшем уменьшении коэффициенты d0 и dn перейдут через ноль, станут отрицательными, а корни (3.28) окажутся положительными. Так как вещественные корни определяют апериодические составляющие решения дифференциального уравнения, то границы (3.27) называют апериодическими границами устойчивости. На самих границах устойчивости корни (3.28) равны соответственно и 0. Стороны кривых, di(,)=0, примыкающие к области положительности соответствующих коэффициентов, штрихуются в сторону положительности. Может случиться так, что какой либо из коэффициентов, d0 или dn не зависит от изменяемых параметров. Это означает отсутствие соответствующей апериодической границы устойчивости.
Колебательной границей устойчивости называется кривая в плоскости изменяемых параметров, при переходе через которую пара комплексно – сопряженных корней изменяет знак своей вещественной части на обратный. Доказано, что колебательная граница устойчивости определяется выражением
![]() (3.29)
(3.29)
В этом выражении n-1 – (n-1) – й определитель Гурвица. Колебательная граница устойчивости штрихуется в сторону положительности n-1.
Пример. Построить область устойчивости в плоскости параметров k и kz системы стабилизации угла тангажа.
Характеристическое уравнение замкнутой системы имеет вид
![]()
Исследуем неравенства d2>0, d3>0, d4>0 . Из первого неравенства следует, что для положительности коэффициента d2 необходимо, чтобы выполнялось условие
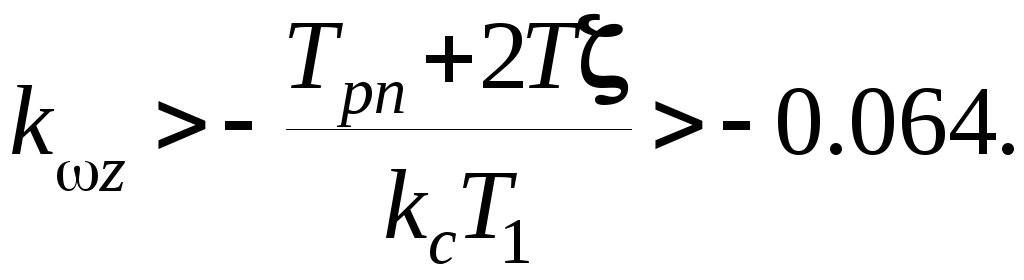
Неравенство d4>0 определяет, что для положительности этого коэффициента необходимо, чтобы k>0. Для выполнения неравенства d3>0 требуется, чтобы
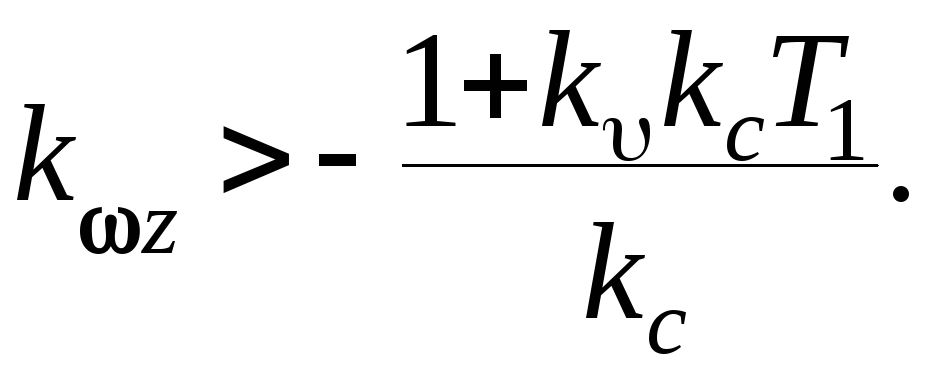
При любых значениях передаточного числа по углу больших нуля, правая часть последнего выражения по модулю будет больше единицы. Таким образом, границами положительности коэффициентов будут
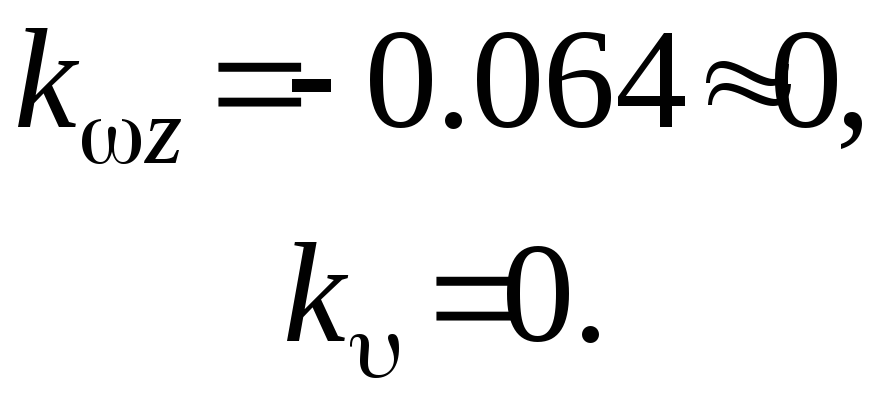
От изменяемых параметров зависит коэффициент dn=d4 и не зависит коэффициент d0. Поэтому уравнение k=0 одновременно является и апериодической границей устойчивости.
Составив определитель Гурвица, для его n-1 минора получим
![]()
Подставим в это выражение значения коэффициентов d2, d3, d4, как функций параметров k и k , после преобразований получим квадратное уравнение, определяющее передаточное число по угловой скорости как функцию от передаточного числа по углу тангажа
![]()
По этому выражению строится колебательная граница устойчивости. График деления области исследуемых параметров на области устойчивости и неустойчивости показан на рис. 3.19.
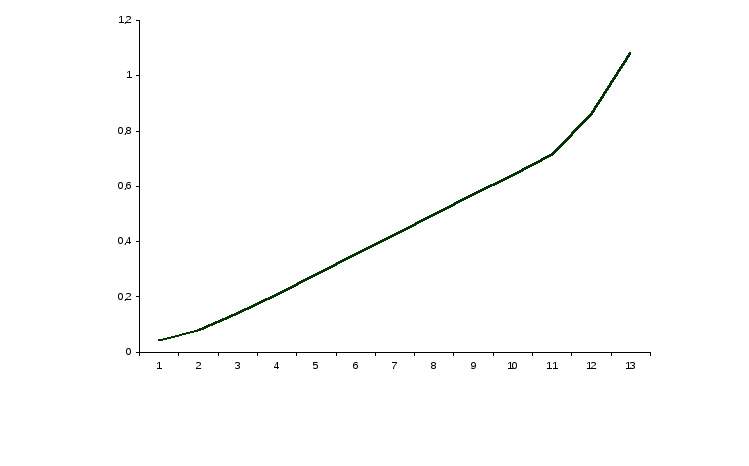
kz















 Область
устойчивости
Область
устойчивости











































































k
Рис.3.19. Область устойчивости системы стабилизации угла тангажа
Граница колебательной неустойчивости штрихуется в сторону положительности n-1- го определителя Гурвица, а прямая kz=0 в сторону положительности этого коэффициента. Для проверки полученных результатов выберем какие – либо значения параметров внутри заштрихованной области, например k=5, kz=0.6, вычислим значения коэффициентов характеристического уравнения и оценим устойчивость замкнутой системы по критерию Гурвица. Получим, что при выбранных значениях передаточных чисел система устойчива. Это означает, что и вся область, внутрь которой обращены штрихи, является областью устойчивости.
3.5.2 D – разбиение в плоскости одного параметра
Пусть нас интересует влияние какого – либо одного параметра на устойчивость САУ и этот параметр входит в характеристическое уравнение линейно, так что это уравнение можно представить в виде
![]() (3.30)
(3.30)
Сделав замену s= j , получим
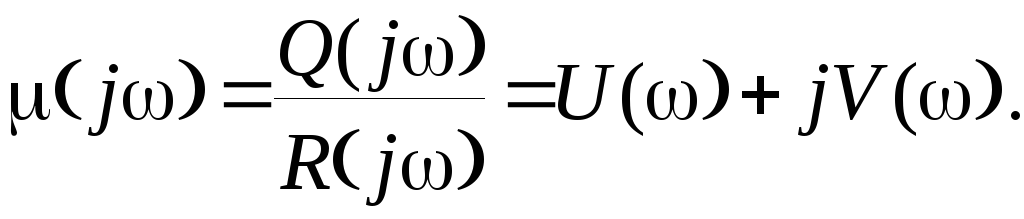 (3.31)
(3.31)
Задавая значения частоты от - до +, можно построить кривую (), отображающую мнимую ось плоскости корней на плоскость . Эта граница D – разбиения симметрична относительно вещественной оси. Поэтому вычисления можно вести в диапазоне частот от 0 до +, а затем дополнить полученную кривую ее зеркальным отображением на диапазон частот от - до нуля. При движении по мнимой оси от - до + на плоскости корней область устойчивости остается слева. Поэтому при движении по кривой D – разбиения в сторону увеличения частоты ее штрихуют слева. Область, внутрь которой обращены штрихи, является предполагаемой областью устойчивости. Для окончательного решения, необходимо взять какое – либо вещественное значение параметра в исследуемой области и воспользоваться каким – либо критерием устойчивости. Если при избранном значении параметра система устойчива, то рассматриваемая область является областью устойчивости.
Пример. Построить область устойчивости системы стабилизации угла тангажа в плоскости передаточного числа k.
Характеристическое уравнение исследуемой системы можно записать в виде
![]()
где
![]()

В полученных выражения сделаем замену s=j и получим


В этих выражениях
![]()
Построенная по этим выражениям кривая D – разбиения показана на рис. 3.20.

 V()
V()








 16.56
16.56

















 5
5
-
U







 ()
()
-



















Рис. 3.20. Область устойчивости в плоскости k.
Так как необходимым условием устойчивости рассматриваемой системы является k>0, то мнимая ось также является границей устойчивости и штрихуется в сторону положительности k. Значение этого коэффициента, равное 5, находится внутри заштрихованной области и мы знаем, что при этом значении система устойчива. Значит и весь отрезок вещественной оси, расположенный внутри заштрихованной области, дает значения передаточного числа по углу, при которых система устойчива. Можно показать, что окончание этого отрезка находиться в точке, равной критическому значению коэффициента k=16.56.
3.5.3. D – разбиение в плоскости двух параметров
Пусть коэффициенты характеристического уравнения линейно зависят от двух параметров и так, что его можно записать в виде
![]() (3.32)
(3.32)
После замены s=j получим
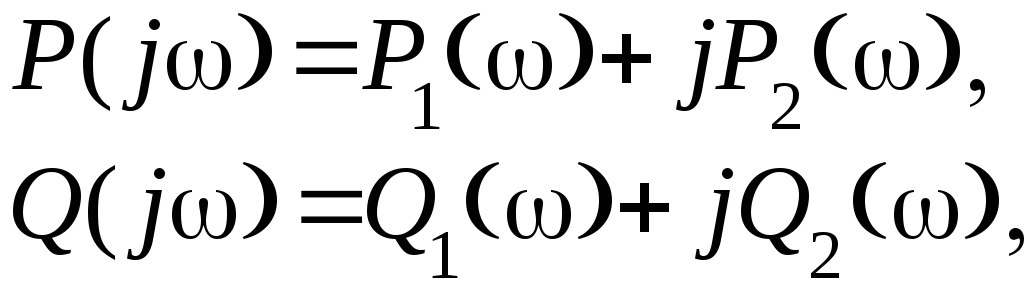
![]()
![]()
Так как равенство нулю всего преобразованного характеристического уравнения может выполняться только, если одновременно равны нулю его вещественная и мнимая части, то получим систему уравнений относительно изменяемых параметров
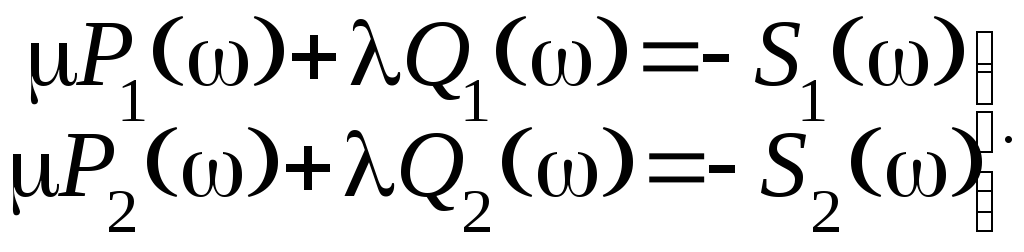 (3.33)
(3.33)
Разрешив систему (3.33) относительно и , получим
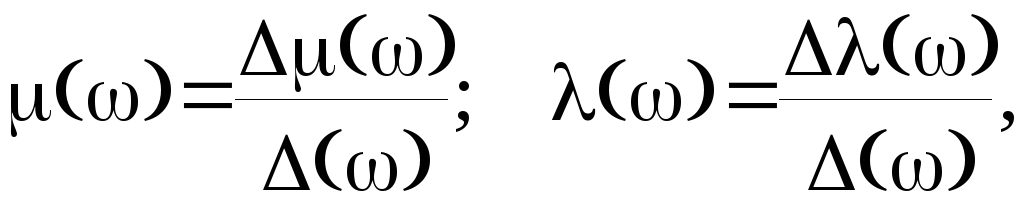
где
![]()
![]()
![]()
Задавая значения частоты от - до +, определим совокупность точек на плоскости - , образующих кривую D – разбиения. Функции () и () являются четными, и поэтому, при изменении частоты в указанных выше пределах, кривая D – разбиения пробегается дважды. При построении кривой D – разбиения в плоскости двух параметров необходимо руководствоваться следующими правилами [8,14]:
1) если в системе (3.33) первое уравнение получено из вещественных частей, а второе – из мнимых частей функций P(j), Q(j) и S(j) и если параметр по написанию стоит первым, а - вторым, то система координат должна быть правой, т.е. ось является осью абсцисс с отсчетом положительных значений вправо, а ось - осью ординат с отсчетом положительных значений вверх;
2)двигаясь по кривой D – разбиения при изменении частоты в сторону увеличения, ее штрихуют слева, если ()>0, и справа, если ()<0; в результате кривая штрихуется дважды с одной стороны, так как на концах кривой при =0 и = знак главного определителя () изменяется.
Может быть случай, когда при =* 0, одновременно (*)= =(*)=(*)=0. Тогда система (3.33) становится линейно – зависимой и ее уравнения отличаются друг от друга только на постоянный множитель. В этом случае эта система сводится к одному уравнению, определяющему на плоскости - прямую линию, которая называется особой прямой. Если особая прямая пересекает кривую D – разбиения в точке =* и в этой точке определитель () меняет знак, то эта прямая также является границей устойчивости и в указанной точке изменяется направление штриховки кривой и особой прямой. Если при =* изменение знака главного определителя не происходит, то штриховка на особую прямую не наносится. Если свободный член характеристического уравнения dn=dn(,), то это соответствует существованию особой прямой для =0 и ее уравнение будет
![]() (3.34)
(3.34)
Уравнение особой прямой для = определяется выражением
![]() (3.35)
(3.35)
Прямые (3.34) и (3.35) называются концевыми. Они штрихуются одинарной штриховкой, согласованной в точках =0 и = с напрвлением штриховки основной линии. Предполагаемая область устойчивости находится внутри заштрихованного участка и проверяется аналогично предыдущему. Переход через кривую D – разбиения, заштрихованную дважды, соответствует переходу через границу устойчивости двух корней, а переход через особую концевую с одинарной штриховкой – переходу одного корня. Если концевые прямые не имеют общих точек с основной кривой, то штриховка на них наносится в сторону положительности параметров.
Пример. Построить область устойчивости системы стабилизации угла тангажа в плоскости параметров k и kz.
Характеристическое уравнение замкнутой системы может быть представлено в виде (3.32), где

После подстановки s=j и выделения вещественных и мнимых частей, получим

Составив систему уравнений (3.33) и решив ее, получим
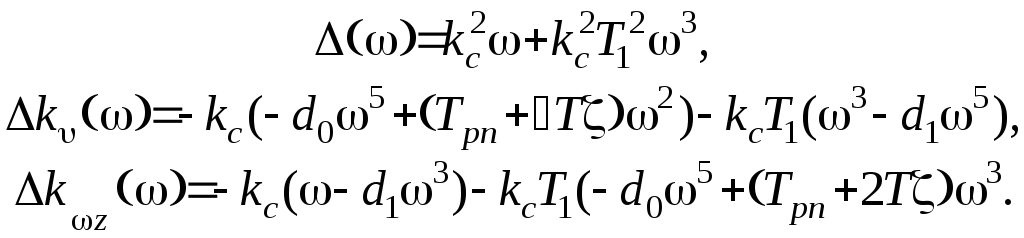
Определив корни этих уравнений, можно сделать вывод, что общих корней, кроме нулевого корня, не существует. Значит особых прямых нет, существует только концевая прямая, соответствующая уравнению dn=kck=0. Руководствуясь выше приведенными правилами, построим кривую D – разбиения и заштрихуем ее и концевую прямую. Проверку осуществим в точке k=5, kz=0.6.

kz




















 Область
устойчивости
Область
устойчивости













































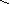















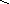














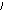
























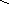



















k
Рис. 3.32. Область устойчивости в плоскости параметров k и kz.
уже ранее установили, что в этой точке система устойчива, а значит и заштрихованная область является областью устойчивости.
