1. Выберем в инструментальной линейке «поверхности и кривые» команду «поверхность вращения» .

1. Выберем в качестве конструктивной плоскости построения плоскость X-Z, если центры оснований конусов лежат в плоскости, параллельной фронтальной плоскости проекций (т.е. В=0).Если нет, то, используя кнопку »параллельная плоскость» укажите плоскость X-Z, а затем расстояние, на которое эта плоскость смещена (В).

2. Построим прямоугольный треугольник с катетами D/2 и H. Для этого в инструментальной линейке «Построения» выбираем команду «Отрезок» , и построим в визуальном режиме треугольник, расположив его примерно в центре системы координат, как это показано на рисунке.

3. С помощью команды «Умный размер» наносим размеры катетов прямоугольного треугольника. Далее задаем ось вращения

Рис.. Эскиз прямоугольного треугольника

После завершения нажимаем кнопку и возвращаемся в среду «Деталь».

4. Зададим угол поворота с помощью кнопки «поворот на 360» в поле «Расстояние» ленточного меню.

В поле построения появится трехмерная модель прямоугольного треугольника. На этом шаге Вы можете поменять ее размеры, выбрав нужный и указав его новое значение в ленточном меню.

Если модель Вас устраивает, нажмите кнопку в ленточном меню.

Рис..

г) Пример построения цилиндра, расположенного вдоль оси Y.

1. Для создания цилиндра воспользуйтесь командой «Поверхность проецирования» в инструментальной линейке «Поверхности и кривые».

2. Выберем конструктивную плоскость построения. В качестве такой плоскости необходимо выбрать плоскость, на которой цилиндр проецируется в окружность. Используя кнопку »параллельная плоскость» укажите плоскость X-Z, а затем расстояние, на которое эта плоскость смещена (В).

3. С помощью команды «Отверстие по центру» построим окружность, задав диаметр, который задан под «D». Центр окружности привяжите к центру координат размерами заданными под буквами «А» и «H»(Рис 11).

Рис. Визуальное изображение окружности

Завершаете операцию нажатием кнопки

7. В поле «Расстояние» ленточного меню задаем высоту «B+80» цилиндра, и выбираем направление формирования поверхности цилиндра (вверх) (Рис. 12).

Рис. Задание направление формирования поверхности цилиндра

Завершаете операцию нажатием кнопки (Рис. 13).

Рис. 13. Результат построения второй поверхности.

Для завершения операции нажатием в ленточном меню кнопку .

3. Пример построения линии пересечения.

1. Выберем в инструментальной линейке «поверхности и кривые» команду «Линия пересечения» .

2. В ленточном меню в графе «Выбор» укажите на слово поверхность.

3. Наведите курсор мыши на конус и нажмите ЛКМ. Выбор подтвердите, нажав на кнопку .

4. Укажите на вторую поверхность и также подтвердите выбор.

5. Создание чертежей.

Загружаем среду «Чертеж»

Нажимаем кнопку «Виды детали» и в появившемся окне указываем деталь или сборочную единицу. Нажимаем кнопку «Открыть»

Переходим в окно «Мастер чертежных видов».

Далее убираем галочки. Нажимаем «Дальше»

Указываем на вид «Спереди» и кнопку «Выбор». Появляется окно главного вида.

Если главный вид нас не устраивает, то используя кнопку , поворачиваем в нужное положение и нажимаем «закрыть». Возвращаемся в окно «Мастер чертежных видов».

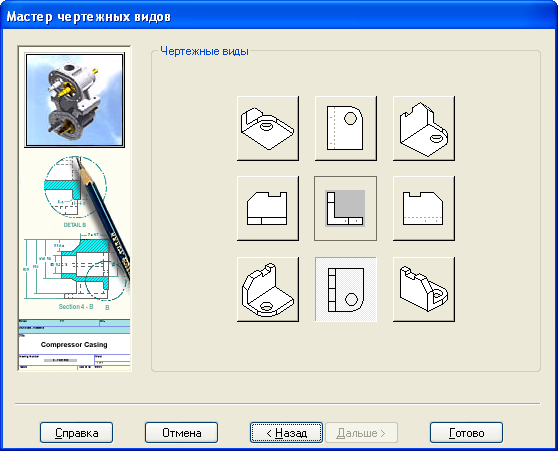
Указываем необходимые виды детали и нажимаем «Готово». Переходим в среду деталь. Указываем масштаб и нажимаем кнопку «параметры отображения детали».

Устанавливаем необходимые стили и нажимаем кнопку «Ок».

Размещаем видовой квадрат приблизительно в середине и нажимаем ЛКМ.

1. Установка атрибутов чертежного вида

2. Выберите элемент на чертежном виде.

3. Поместите курсор на рамку чертежного вида и щелкните ЛКМ.

4. В меню "Правка" выберите команду "Атрибуты".

5. В диалоговом окне атрибутов задайте требуемые параметры.

Нажмите кнопку «Ок».

Далее проставляем необходимые размеры и оси симметрии.

Далее заполняем основную надпись.

РАЗВЕРТКА ПОВЕРХНОСТИ.

Разверткой называется плоская фигура, полученная совмещением поверхности тела с плоскостью.

Для построения многогранной поверхности необходимо совместить с плоскостью все ее грани. Для построения развертки поверхности в общем случае надо в нее вписать многогранную поверхность и совместить с плоскостью. Поверхности, которые разворачиваются на плоскость без разрывов и складок, называются развертываемыми. К ним относятся линейчатые поверхности, у которых образующие параллельны или пересекаются (цилиндры, торсы, конусы). Остальные поверхности неразвертываемые. Развертки обладают многими одинаковыми свойствами самих поверхностей: равенством длинами прямых, равенством углов между линиями, параллельностью прямых. Развертки простых фигур можно строить и математически. Для цилиндра - это прямоугольник с длиной S = 2pR; для конуса - сектор с углом при вершине j= 2 pR / l (l - длина образующей). Однако чаще это сложные поверхности с вырезами и срезами на них, развертки которых возможно только использую графические приемы. Основной метод графического построения разверток - это аппроксимация заданной поверхности в виде многогранной поверхности. Часто вписывают многогранник с гранями в виде треугольников. Данный способ называется способом триангуляции. Самой трудоемкой частью при построении разверток является определение натуральной величины граней вписываемого в поверхность многогранника. Имеется ряд способов и приемов, сокращающих эту работу и облегчающих построение разверток. К ним относятся способ треугольников, способ нормального сечения и способ раскатки, которые, в свою очередь, используют, методы определения натуральной величины граней методами замены плоскостей проекций (ортогонального проецирования по нормали к плоскости грани) или вращения вокруг проецирующих осей.

Развертка конусов производится по принципу развертывания пирамиды, для чего поверхность конуса предварительно аппроксимируют n - гранной пирамидой. На рис. выполнено построение развертки наклонного конуса. Основание конуса разделено на 8 частей. Натуральные величины образующих определены методом вращения.

Для построения ее используем то, что очерковая образующая конуса L на фронтальной плоскости изобразилась в натуральную величину. Выбрав положение вершины развертки — точку S, радиусом L проводим дугу и откладываем на ней 12 равных частей, на которые предварительно разделили окружность основания конуса, изображенного на горизонтальной плоскости проекции в натуральную величину. Чем на большее количество равных участков разделим окружность, тем точнее построим развертку. Положение точки М на развертке поверхности конуса определим следующим образом: через фронтальную проекцию точки проведем образующую и построим ее горизонтальную проекцию. Найдем, что образующая пересекла основание конуса между точками 5 и 6. Точку К переносим на дугу развертки, расположив ее между точками 5 и 6, и соединим с вершиной конуса развертки S. Из проекции точки M₂ проведем горизонтальную линию до пересечения с очерковой образующей L и получим точкуМ₂. Расстояние от основания конуса до точки M₂ по образующей является высотой точки, которую откладываем на развертке от точки К на линии KS. Полученная точка определит истинное положение точки M на развертке. Таким образом, развертку конической поверхности построим с помощью соседних точек окружности основания, в которую вписан правильный двенадцатиугольник, т. е. коническая поверхность условно заменена поверхностью, вписанной правильной двенадцатиугольной пирамидой, а для построения развертки применен способ триангуляции.

Задание выполнено.