Реализация типовых динамических звеньев.

В радиотехнике наибольшее распространение получила реализация динамических звеньев на операционных усилителях.

Операционный усилитель – устройство, умеющее высокий коэффициент усиления дифференциального сигнала, высокое входное сопротивление и низкое выходное сопротивление.

Большинство решающих элементов строят по единой общей схеме, охватывая операционный усилитель обратной связью. Обратная связь позволяет формировать амплитудную характеристику, соответствующую реализации заданной математической функции. Непосредственный анализ и расчет таких схем с учетом неидеальности свойств ее отдельных частей достаточно сложен. Поэтому в настоящее время сначала проектируют решающие элементы с учетом идеализированных операционных усилителей и последующим уточнением решений путем вычисления возникающих ошибок. При необходимости проверяется устойчивость работы устройства.

Отличительной особенностью операционного усилителя является то, что он имеет два входа. В зависимости от подачи сигнала на инвертирующий или неинвертирующий вход выходное напряжение относительно входного имеет фазовый сдвиг 0 или π радиан. Это свойство широко используют при составлении схем на операционных усилителях.

Анализ свойств операционного усилителя, охваченного параллельной обратной связью, по инвертирующему входу в первом приближении дает выражение для коэффициента передачи системы.

Д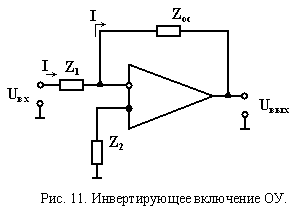ля идеализированного ОУ (R_вх= ∞,K_оу= ∞):

отсюда:

Источники сигнала и входные сопротивления можно подключать и к неинвертирующему входу ОУ.

При замкнутой цепи обратной связи:

при совместном решении этих равенств, учитывая, что K_оу= ∞, получим:

Выполняя комплексные сопротивления из различных соединений RиC, можно придать устройству любую необходимую частотную характеристику. Это может быть безынерционное звено с необходимым коэффициентом передачи, интегрирующее или дифференцирующее звено и др.

Рис. 13. Реализация безынерционного звена на ОУ.

Так, безынерционное звено может быть реализовано как с помощью инвертирующего (Рис. 13. А), так и с помощью неинвертирующего включения (Рис. 13. Б).

По тому же принципу на ОУ могут быть реализованы сумматор и элемент сравнения (вычитатель):

Рис. 14. Инвертирующий сумматор (А) и вычитатель (Б) на ОУ.

Реализовать интегрирующее и дифференцирующее звенья можно по схемам на Рис.14. А и Б соответственно.

Рис. 15. Интегрирующее (А) и дифференцирующее (Б) звенья на ОУ.

Реализация апериодического звена первого порядка и звена второго порядка показана на Рис. 15. А и Б соответственно.

Для апериодического звена первого порядка:

Для звена второго порядка:

Поставив после этого звена интегратор и подобрав номиналы элементов, можно получить типовое колебательное звено или типовое апериодическое звено второго порядка.

Рис. 16. Апериодическое звено 1-ого порядка (А) и звено 2-ого порядка (Б) на ОУ.

Передаточные функции систем радиоавтоматики и кибернетики.

При исследовании автоматической системы составляют ее схему, в которой указывают все функциональные элементы системы и связи между элементами. Такую схему называют функциональной.

Однако при анализе процессов управления имеет значение не функциональное значение элементов системы, а их динамические характеристики, заданные в виде дифференциальных уравнений, а для линейных систем – в виде передаточных функций этих элементов. Поэтому составляют схему автоматической системы, в которой указывают динамические звенья системы и связи между ними. Такую схему называют структурнойсхемой автоматической системы. Ее получают из функциональной, замещая обоз­начения функциональных элементов системы обозначениями или яв­ными выражениями передаточных функций этих элементов.

Структурная схема автоматической системы позволяет получить передаточную функцию или дифференциальное уравнение этой сис­темы при известных динамических характеристиках ее звеньев.

При определении передаточной функции достаточно сложной авто­матической системы ее структурную схему упрощают, пользуясь ме­тодами преобразования структурных схем, позволяющими перейти от сложных перекрестных соединений звеньев в системе к некоторым простейшим, типовым соединениям. Существует три вида таких сое­динений: последовательное,параллельноеивстречно-параллельное, или охват обратной связью одного звена посредством другого.

Последовательнымназывают такое соединение звеньев, при котором выходная величина одного звена является входной величиной другого (см. Рис. 17.).

Рис. 17. Последовательное соединение звеньев.

При последовательном соединении звеньев переда­точная функция такого соединения равна произведению передаточных функций отдельных звеньев:

Это выражение справедливо при условии, что соединение выхода каждого i-ого звена со входом следующего, (i+1)-ого звена не изменяет передаточную функцию i-ого звена. В противном случае передаточную функцию W_i(p) i-ого звена нужно составлять с учетом влияния сле­дующего звена.

Рис. 18. Различные соединения звеньев (параллельное и с обратной связью соответственно).

При параллельномсоединении звеньев входная величинаx₁(t) поступает на входы всех звеньев, входящих в это соединение, а выходная вели­чина x₂(t) равна сумме выходных величин отдельных звеньев (см. Рис. 18.), значит:

Схема звена, охваченного обратной связью, показана на Рис. 18. Как видно из схемы, на вход звена с передаточной функ­цией W₁(p), охваченного обратной связью посредством звена с пере­даточной функцией W₂(p), поступает сумма или разность (в зависимо­сти от характера обратной связи) двух величин – входнойx₁(t) и выходной x₂(t), прошедшей через звено обратной связи. Тогда выражение для передаточной функции выглядит так:

где знак минус соответствует положительной обратной связи, а знак плюс — отрицательной.

Рассматривая структурные схемы линейных автоматических систем, видим, что лю­бая структурная схема состоит из элементов трех типов: звеньев, уз­лов и сумматоров, соединенных между собой связями. Элемент сравнения (вычитатель), имеющийся в сос­таве структурной схемы, является частным случаем сумма­тора, на выходе которого образуется разность двух его входных вели­чин.

Если в структурной схеме исследуемой системы имеется участок, содержащий сложные перекрестные связи, не сводящиеся к рассмо­тренным простейшим соединениям звеньев, то этот участок выделяют и подвергают структурным преобразованиям с целью приведения всех его соединений к простейшим типовым. Структурные преобразования состоят в изменении взаимного расположения элементов структурной схемы (звеньев, узлов и сумматоров) таким образом, чтобы, не изме­няя входных и выходных величин преобразуемого участка схемы, изменить (упростить) характер соединений его звеньев.

Правила изменений взаимного расположения элементов структур­ной схемы определяются табл. 2. Смысл этих правил на можно уяснить на при­ме (см. Рис. 19.).

Рис. 19. Пример структурного преобразования схем.

Не трудно убедиться, что общая передаточная функция при структурных преобразованиях остается неизменной.

Таблица 2. Правила преобразования структурных схем линейных систем.

Пример: Рассмотрим структурную схему Рис. 20. В этой схеме пере­крестные связи обусловлены наличием между сумматорами 1 и 2 звена W_4.

Рис. 20. Схема к примеру.

Чтобы избавиться в этой схеме от перекрестных связей, достаточно, например, сумма­тор 1 перенести со входа звена W₄ на его выход. При этом получим схему Рис. 21

Рис. 21. Структурное преобразование схемы на Рис. 20.

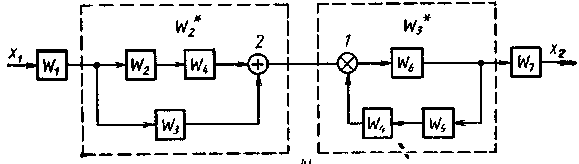
Рис. 22. Структурное преобразование схемы на Рис. 21.

Поменяв сумматоры местами, придем к схеме Рис. 22, для которой можно без особого труда найти передаточную функцию, учитывая, что:

При исследовании автоматических систем возникают различные задачи, например, определение характеристик переходного процесса в системе, определение ее точности, помехоустойчивости и т. д. Решение этих задач требует установления зависимости между различными переменными автоматической системы, например между выходной и выходной величинами системы, между ошибкой и входной величиной и т. д. Эти зависимости устанавливаются посредством соответствующих передаточных функций автоматической системы.

Для анализа работы системы радиоавтоматики применяют представление системы структурной схемой, приведенной на Рис. 23.

Рис. 23. Типичная структурная схема исследуемых систем.

Здесь – входное воздействие,– возмущение, точкой приложения делящее прямую ветвь системы на два звена с передаточными функциямии. При исследовании системы необходимо располагать:

1. Передаточной функцией разомкнутой системы.

где – коэффициент передачи (добротность) системы поl-ой производной входного воздействия;m– число форсирующих звеньев;n –порядок характеристического уравнения, причемn>m;(n-l)– число апериодических звеньев;l – число интеграторов (порядок астатизма системы).

2. Передаточной функцией замкнутой системы

3. Передаточной функцией для ошибки по воздействию

4. Передаточной функцией для ошибки по возмущению (помехе).

В частности, если помеха действует на входе системы, то