4. Объем многомерного параллелепипеда.

Найдем площадь параллелограмма, образованного двумя направленными отрезками и с общим началом в точке – начале координат. Для этого разложим, например, : . Искомая площадь равна . Назовем эту площадь «двумерным объемом» или объемом системы векторов ,; обозначение: . Очевидно, что в том и только в том случае, если и коллинеарны.

Найдем объем параллелепипеда, образованного тремя направленными отрезками ,, с общим началом в точке – начале координат. Для этого используем, например, разложения и . Искомый объем равен . Очевидно, что в том и только в том случае, если ,, лежат в одной плоскости (такие направленные отрезки называют компланарными).

Вообще, пусть – элементы евклидова пространства , . Снова будем пользоваться обозначениями , причем под будем подразумевать нулевое подпространство пространства . Ясно, что в разложении . Назовем объемом -мерного параллелепипеда, образованного векторами , произведение чисел: . Очевидно, что в том и только в том случае, если система векторов линейно зависима.

5. Метрические пространства.

Наличие скалярного произведения в линейном пространстве позволяет ввести в нем евклидову норму (длину) вектора и евклидово расстояние между точками. Однако, часто требуется измерять длины и расстояния по-другому, в ином смысле. Рассмотрим наиболее общий подход к измерению расстояний между точками.

Пусть – произвольное множество, не обязательно линейное пространство. Говорят, что в введено расстояние между его элементами ( точками), если каждой паре элементов поставлено в соответствие действительное число , причем выполнены следующие аксиомы:

1. для любых .

2. , если ; если .

3. для любых .

Такая функция двух переменных называется расстоянием или метрикой. Множество с метрикой называется метрическим пространством.

Примеры метрических пространств.

1. , .

2. – произвольное множество, 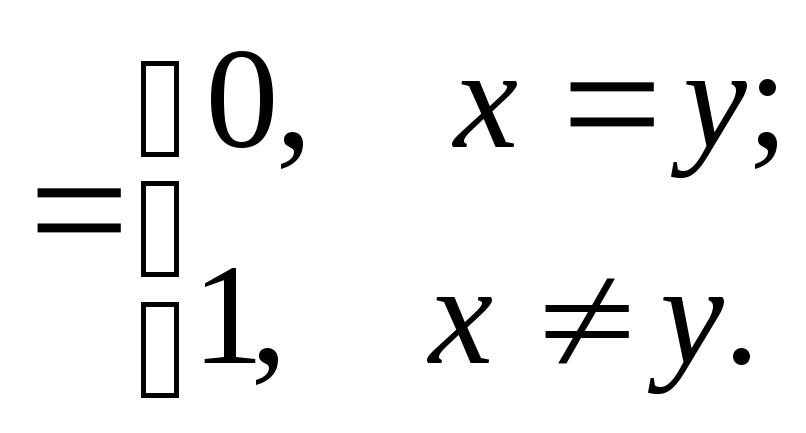Такое метрическое пространство называется пространством изолированных точек.

3. , .

4. , но расстояние введено отличным от примера 3 способом: .

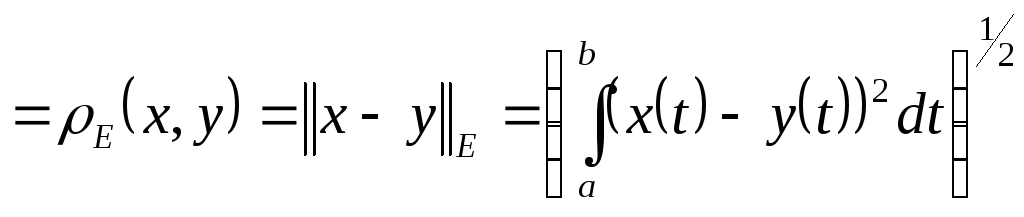5. , .

6. , но расстояние введено отличным от примера 5 способом: .

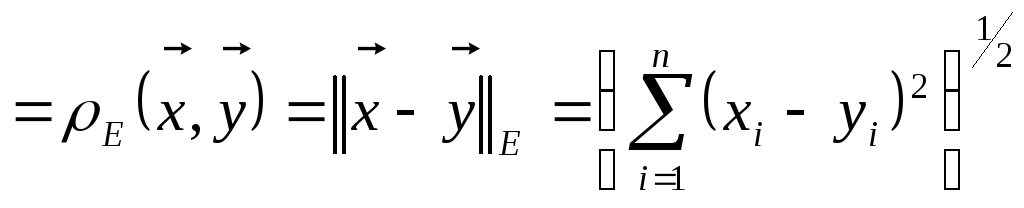Задача. Проверьте, что в приведенных примерах выполнены аксиомы метрики.¨

Наличие метрики во множестве позволяет ввести понятие предела последовательности элементов этого множества.

Определение. Пусть – бесконечная последовательность элементов множества . Элемент называется пределом последовательности , если для любого действительного числа найдется такой номер, что при всех выполнены неравенства .

Задача. Сформулируйте определение фундаментальной последовательности элементов метрического пространства.

Замечание. Критерий Коши справедлив не во всех метрических пространствах!

Одна и та же последовательность может быть сходящейся в одной метрике и расходящейся в другой метрике. Например, если , , то в метрике примера 1 эта последовательность сходится к числу . Но в метрике примера 2 такая последовательность не имеет предела, поскольку она состоит из попарно различных элементов.

Множество всех элементов метрического пространства, которые удовлетворяют неравенству ( – некоторый фиксированный элемент), называется открытым шаром радиуса с центром . Множество всех элементов , удовлетворяющих неравенству , называется замкнутым шаром. Множество метрического пространства называется ограниченным, если оно целиком содержится в некотором шаре конечного радиуса (т.е. существуют такой элемент и такое число , что для всех выполнено неравенство ).

Задача. Функция задана на метрическом пространстве (). Сформулируйте определение непрерывности этой функции в точке в смысле метрики .