Тема 4. Евклидовы и нормированные пространства.
1. Скалярное произведение и евклидова норма.
Через
будем обозначать в данном разделе
действительное линейное пространство
(поле чисел
).
Введем в
функцию двух переменных: каждой паре
элементов
поставим в соответствие действительное
число
.
Такая функция называется скалярным
произведением, если выполнены следующие
аксиомы:
1.
для всех
.
2.
для всех
.
3.
для всех
и любого числа
.
4.
,
если
;
.
Примеры.
1. В качестве
возьмем линейное пространство
геометрических векторов (направленных
отрезков). Скалярное произведение в
можно задать в виде
,
где
и
– длины направленных отрезков
и
,
а
– угол между ними.
2.
– линейное пространство всех действительных
непрерывных на отрезке
функций (
означает, что функция
непрерывна в каждой точке
).
Двум таким функциям
и
поставим в соответствие их скалярное
произведение по формуле
.
В том же линейном пространстве
скалярное произведение можно ввести
по-другому. Фиксируем, например, некоторую
положительную непрерывную функцию
(
для
всех
).
Под скалярным произведением функций
и
будем понимать
.
В частности, можно выбрать
.
3.
.
Двум векторам-строкам
и
из пространства
поставим в соответствие их скалярное
произведение
.
В том же линейном пространстве
скалярное произведение можно ввести
по-другому. Фиксируем числа
.
Под скалярным произведением элементов
и
будем понимать
.
В частности, можно выбрать
.
Задача. В приведенных выше примерах проверьте выполнение всех аксиом скалярного произведения.
Определение. Действительное линейное пространство со скалярным произведением называется евклидовым пространством.
Теорема
1. Для любых двух элементов
евклидова пространства справедливо
неравенство Коши-Буняковского:
.
Доказательство.
Пусть
– произвольные элементы евклидова
пространства, а
– любое число. По аксиомам скалярного
произведения
.
В левой части этого неравенства написан
квадратный трехчлен относительно
.
Он неотрицателен при всех
в том и только в том случае, если его
дискриминант
.
Отсюда и получаем
.
Величина
называется евклидовой нормой
элемента
.
Введем для нее специальное обозначение:
.
Теорема 2. Евклидова норма обладает следующими свойствами:
1.
,
если
;
,
если
.
2.
для любого элемента
и любого числа
.
3.
для любых элементов
.
(Докажите самостоятельно.)
Евклидова норма
направленного отрезка – это его длина
( см. пример 1). Евклидова норма элемента
абстрактного евклидова пространства
тоже имеет смысл длины этого элемента.
Если в действительном линейном
пространстве введено скалярное
произведение, то кроме длин его элементов
можно ввести понятие угла
между ненулевыми элементами
и
и евклидова расстояния
между любыми элементами
и
.
Угол
между векторами
и
определяется из условий
,
.
Евклидовым расстоянием между точками
и
называется
.
Теорема 3. Евклидово расстояние обладает следующими свойствами:
1.
для любых элементов
.
2.
,
если
;
,
если
.
3.
для любых элементов
.
(Докажите самостоятельно.) Свойство 3 расстояния называется неравенством треугольника.
Замечание.
Если в пространстве
введено скалярное произведение
,
то неравенство Коши-Буняковского
означает, что
для
любых
.
Замечание.
Если в пространстве
введено скалярное произведение
,
то неравенство Коши-Буняковского
означает, что
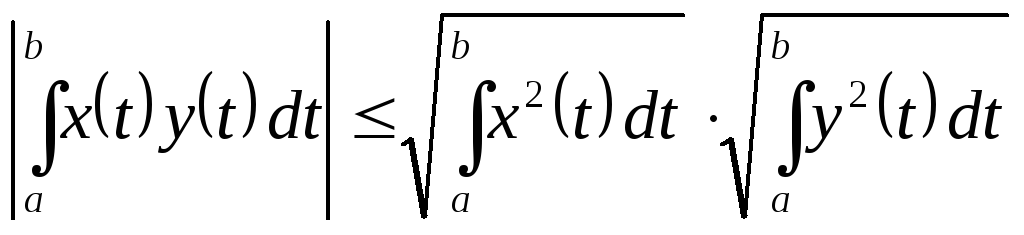для любых
.
Задача.
Векторы
и
называются коллинеарными, если
существует такое число
,
что
,
или существует такое число
,
что
.
Докажите, что неравенство Коши-Буняковского
обращается в равенство в том и только
в том случае, если
и
коллинеарны.