4. Геометрическая интерпретация множества решений.

Опишем с точки зрения теории линейных пространств множество всех решений однородной системы

(4)

и неоднородной системы (1)

Теорема 6. Множество всех решений однородной системы (4) образует в пространстве линейное подпространство размерности .

Доказательство. Обозначим через множество всех решений системы (4): . Пусть . Тогда для любых получим , т.е. – линейное подпространство в .

Найдем . Снова будем предполагать, что , и что базисный минор матрицы находится в ее левом верхнем углу (этого можно добиться перенумерацией неизвестных и перестановкой уравнений). Тогда являются свободными неизвестными. Пусть ; поставим в соответствие этому решению системы (4) вектор-столбец . Такое соответствие между элементами и взаимно однозначно и является линейным изоморфизмом. Поэтому .

Из теоремы 6 видно, что если и , т.е. , то (см. теорему 5).

В линейном пространстве решений системы (4) выберем какой-нибудь базис:

. Тогда любое решение системы (4) имеет вид .

Определение. Любые линейно независимых решений системы (4) называются фундаментальной системой решений.

Пример фундаментальной системы решений.

Если, как предполагалось выше, и базисный минор матрицы находится в ее левом верхнем углу, то фундаментальной системой решений (4) является, например,

, ,

,. Здесь

определяются однозначно из систем уравнений вида (3), в которых . В качестве значений свободных неизвестных в этих системах берутся

.

Можно вместо указанного базиса в взять любой другой базис. Тогда получим другую фундаментальную систему решений (4).

Теорема 7. Общее решение неоднородной системы (1) () является суммой общего решения соответствующей однородной системы (4) и произвольного частного решения неоднородной системы (1).

Доказательство. Пусть , а – частное решение неоднородной системы: . Тогда . С другой стороны, если и таковы, что и , то , т.е. .

Теорема 7 показывает, что общее решение неоднородной системы (1) получается сдвигом множества на произвольный вектор , который удовлетворяет условию. При этом результат сдвига не зависит от выбора конкретного такого , поскольку речь идет о всем множестве в целом.

Теорема 7* (другая формулировка). Общее решение неоднородной системы (1) представляет собой плоскость размерности в пространстве . Ее направляющим подпространством является , а в качестве вектора сдвига можно взять любое частное решение системы (1).

5. Метод Гаусса.

Метод Гаусса (или метод последовательного исключения неизвестных) приводит систему уравнений (1) к эквивалентной системе наиболее простого вида. Опишем выполнение элементарных преобразований системы (1) по шагам.

Предположим, что в (1) коэффициент . Если среди коэффициентов есть отличные от нуля, то этого всегда можно добиться, переставляя, в случае необходимости, уравнения и (или) изменяя нумерацию неизвестных. Умножим первое уравнение на и вычтем его из второго уравнения. Затем умножим первое уравнение на и вычтем его из третьего уравнения. И так далее. В результате получим систему уравнений

()

Коэффициент называют ведущим элементом первого шага. В системе () первое уравнение совпадает с первым уравнением исходной системы (1), а из остальных уравнений мы исключили .(Выразите все коэффициенты и свободные члены через коэффициенты и свободные члены исходной системы (1).)

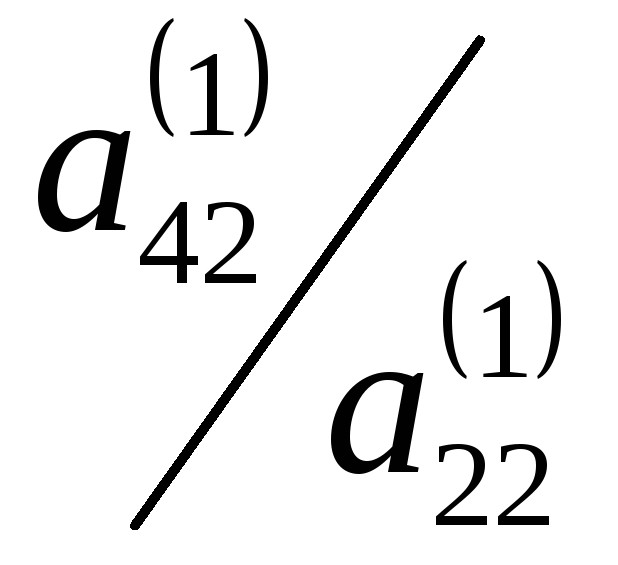Предположим, что в () коэффициент . Если среди коэффициентов , , , есть отличные от нуля, то этого всегда можно добиться, переставляя, в случае необходимости, уравнения с номерами и (или) изменяя нумерацию неизвестных с теми же номерами. Умножим второе уравнение в () на и вычтем его из третьего уравнения в (). Затем умножим второе уравнение в () на и вычтем его из четвертого уравнения в (). И так далее. В результате получим систему уравнений

()

Коэффициент называют ведущим элементом второго шага. В системе () два первых уравнения совпадают с первыми двумя уравнениями системы (), а из остальных уравнений мы исключили и .(Выразите все коэффициенты и свободные члены через коэффициенты и свободные члены системы ().)

В конечном счете, выполнив некоторое число шагов описанных преобразований, мы получим систему уравнений

()

Здесь , , . Если среди чисел есть отличные от нуля, то система () несовместна; тогда и исходная система (1) несовместна. Несовместность системы (1) можно было обнаружить и раньше, если на некотором шаге получилось бы уравнение , где . Если , то система () совместна. Для отыскания её решений достаточно использовать только первые уравнений. В случае получаем систему треугольного вида; она имеет единственное решение: из -го уравнения однозначно определяем , подставляя его в предыдущее уравнение, однозначно определяем , и т.д. В случае получаем трапециевидную систему; она имеет бесконечно много решений: неизвестные являются свободными. В этом случае, придавая свободным неизвестным произвольные значения , мы получим относительно неизвестных систему уравнений с невырожденной треугольной матрицей, решить которую можно указанным только что способом.

Очевидно, что описанными элементарными преобразованиями системы (1) мы находим ранг её основной матрицы. Базисный минор основной матрицы преобразованной системы () окажется в eё левом верхнем углу. По-другому выбирая ведущие элементы на каждом шаге метода Гаусса, можно на -ом шаге получить систему другой конфигурации.