
- •Тема 3. Системы линейных алгебраических уравнений.
- •1. Системы линейных алгебраических уравнений.
- •2. Системы с невырожденной квадратной матрицей.
- •3. Критерий совместности системы. Общее решение. Критерий единственности решения.
- •4. Геометрическая интерпретация множества решений.
- •5. Метод Гаусса.
- •Тема 4. Евклидовы и нормированные пространства.
- •1. Скалярное произведение и евклидова норма.
- •2. Унитарное пространство.
- •3. Ортогональность.
- •4. Объем многомерного параллелепипеда.
- •5. Метрические пространства.
- •6. Линейные нормированные пространства.
Тема 3. Системы линейных алгебраических уравнений.
1. Системы линейных алгебраических уравнений.
Системой
![]() линейных алгебраических уравнений с
линейных алгебраических уравнений с
![]() неизвестными называется совокупность
уравнений
неизвестными называется совокупность
уравнений
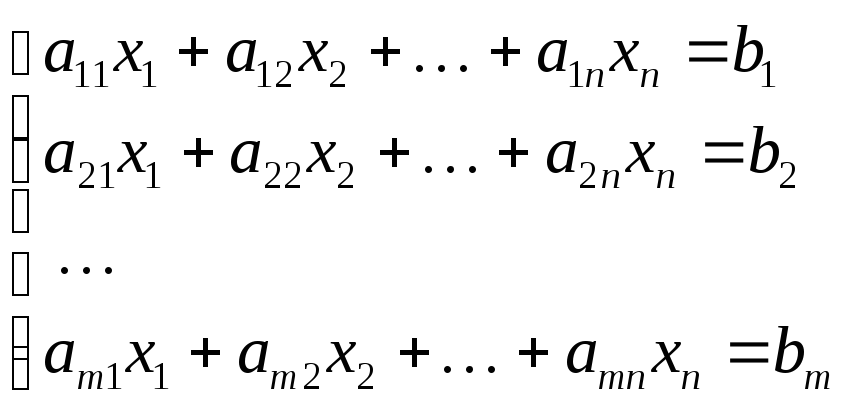 (1)
(1)
относительно искомых величин
![]() ;
коэффициенты системы
;
коэффициенты системы
![]() ,
свободные члены
,
свободные члены
![]() и неизвестные
и неизвестные
![]() суть числа из одного и того же поля
суть числа из одного и того же поля
![]() (
(![]() или
или
![]() ).
Если при подстановке чисел
).
Если при подстановке чисел
![]()
![]() во все уравнения (1) вместо
во все уравнения (1) вместо
![]() все эти уравнения обращаются в тождества,
то совокупность таких чисел называется
решением системы (1). Система уравнений
(1) называется совместной, если она имеет
хотя бы одно решение
все эти уравнения обращаются в тождества,
то совокупность таких чисел называется
решением системы (1). Система уравнений
(1) называется совместной, если она имеет
хотя бы одно решение
![]() ;
если же система не имеет ни одного
решения, то она называется несовместной.
Кроме вопроса о существовании решений
у системы (1) нас будет интересовать,
единственно ли найденное решение.
;
если же система не имеет ни одного
решения, то она называется несовместной.
Кроме вопроса о существовании решений
у системы (1) нас будет интересовать,
единственно ли найденное решение.
Введем матрицу
![]() коэффициентов системы (1):
коэффициентов системы (1):
![]() (
(![]() называется основной матрицей
системы). Неизвестные и свободные члены
будем записывать в виде векторов-столбцов:
называется основной матрицей
системы). Неизвестные и свободные члены
будем записывать в виде векторов-столбцов:
![]()
![]() ,
,
![]()
![]() .
Тогда систему линейных алгебраических
уравнений (1) можно коротко записать в
виде
.
Тогда систему линейных алгебраических
уравнений (1) можно коротко записать в
виде
![]() .
Ту же систему можно представить и в виде
.
Ту же систему можно представить и в виде
![]() ,
где
,
где
![]() –
векторы-столбцы матрицы
–
векторы-столбцы матрицы
![]() ,
,
![]() .
Нас интересует ответ на вопрос: является
ли вектор-столбец
.
Нас интересует ответ на вопрос: является
ли вектор-столбец
![]() линейной комбинацией векторов-столбцов
линейной комбинацией векторов-столбцов
![]() ?
Или, что то же самое, принадлежит ли
?
Или, что то же самое, принадлежит ли
![]() линейной оболочке
линейной оболочке
![]() ?
Если существуют такие
?
Если существуют такие
![]() ,
что
,
что
![]()
![]() ,
т.е.
,
т.е.
![]()
![]()
![]() ,
то следующим будет вопрос: является ли
такое разложение вектора-столбца
,
то следующим будет вопрос: является ли
такое разложение вектора-столбца
![]() по системе векторов-столбцов
по системе векторов-столбцов
![]() единственным; в случае неединственности
решений надо описать множество всех
решений системы (1). Мы увидим, что ответы
на поставленные вопросы достаточно
просты и допускают геометрическую
интерпретацию.
единственным; в случае неединственности
решений надо описать множество всех
решений системы (1). Мы увидим, что ответы
на поставленные вопросы достаточно
просты и допускают геометрическую
интерпретацию.
В процессе построения решений системы (1) эту исходную систему приходится преобразовывать; при этом важно сохранить множество ее решений. Две системы линейных алгебраических уравнений с одинаковым числом неизвестных называются эквивалентными, если множества всех их решений совпадают.
Теорема
1. Если
![]() –
невырожденная
–
невырожденная
![]() -матрица,
то системы
-матрица,
то системы
![]() и
и
![]() эквивалентны.
эквивалентны.
Доказательство.
Пусть
![]() – решение системы
– решение системы
![]() ,
т.е.
,
т.е.
![]() .
Тогда, очевидно,
.
Тогда, очевидно,
![]() .
.
Пусть теперь
![]() – решение второй системы, т.е.
– решение второй системы, т.е.
![]() .
В силу невырожденности матрицы
.
В силу невырожденности матрицы
![]() существует обратная к ней матрица
существует обратная к ней матрица
![]() .
И тогда
.
И тогда
![]() ,
что означает
,
что означает
![]() .
.
2. Системы с невырожденной квадратной матрицей.
Рассмотрим
частный случай:
![]() .
.
Теорема
2. Пусть
![]() ,
и основная матрица
,
и основная матрица
![]() системы (1) не вырождена. Тогда система
(1) совместна, и ее решение единственно.
системы (1) не вырождена. Тогда система
(1) совместна, и ее решение единственно.
Доказательство.
Из невырожденности матрицы
![]() вытекает существование обратной к ней
матрицы
вытекает существование обратной к ней
матрицы
![]() .
Тогда из
.
Тогда из
![]() имеем
имеем
![]() ,
т.е.
,
т.е.
![]() .
Очевидно, что других решений нет: если
еще
.
Очевидно, что других решений нет: если
еще
![]() ,
то
,
то
![]() ,
,
![]() ,
,
![]() .
.
Если
![]() – квадратная невырожденная матрица,
то
– квадратная невырожденная матрица,
то
![]() ,
где
,
где
![]() – матрица, присоединенная к
– матрица, присоединенная к
![]() .
.
![]() составлена
из алгебраических дополнений
составлена
из алгебраических дополнений
![]() к элементам
к элементам
![]() матрицы
матрицы
![]() и транспонирована. Поэтому
и транспонирована. Поэтому
![]() для всех
для всех
![]() .
Это можно записать в виде
.
Это можно записать в виде
![]() ,
где матрица
,
где матрица
![]() получается из матрицы
получается из матрицы
![]() заменой ее
заменой ее
![]() -го
столбца на вектор-столбец ее свободных
членов
-го
столбца на вектор-столбец ее свободных
членов
![]() .
Такой способ построения решений
называется правилом Крамера.
.
Такой способ построения решений
называется правилом Крамера.
3. Критерий совместности системы. Общее решение. Критерий единственности решения.
Припишем к
основной матрице
![]() системы (1) вектор-столбец
системы (1) вектор-столбец
![]() ;
полученную
;
полученную
![]() -матрицу
называют расширенной матрицей
системы (1):
-матрицу
называют расширенной матрицей
системы (1):
![]() .
.
Теорема
3. (Теорема Кронекера-Капелли).
Система линейных алгебраических
уравнений (1) совместна в том и только в
том случае, если
![]() .
.
Доказательство.
Необходимость.
Совместность системы
![]() означает, что существуют числа
означает, что существуют числа
![]()
![]() ,
для которых справедливо равенство
,
для которых справедливо равенство
![]()
![]() .
То есть, вектор-столбец
.
То есть, вектор-столбец
![]() является линейной комбинацией
векторов-столбцов
является линейной комбинацией
векторов-столбцов
![]() матрицы
матрицы
![]() .
Поэтому
.
Поэтому
![]() .
.
Достаточность.
Пусть
![]() .
Выберем в матрице
.
Выберем в матрице
![]() какой-либо ее базисный минор. Тогда
этот же минор является базисным минором
матрицы
какой-либо ее базисный минор. Тогда
этот же минор является базисным минором
матрицы
![]() .
Поэтому вектор-столбец
.
Поэтому вектор-столбец
![]() можно представить в виде линейной
комбинации всех векторов-столбцов
матрицы
можно представить в виде линейной
комбинации всех векторов-столбцов
матрицы
![]() .
Коэффициенты этой линейной комбинации
образуют решение системы (1).
.
Коэффициенты этой линейной комбинации
образуют решение системы (1).
Выберем в матрице
![]() какой-либо ее базисный минор. Ради
удобства перенумеруем неизвестные
какой-либо ее базисный минор. Ради
удобства перенумеруем неизвестные
![]() и свободные члены
и свободные члены
![]() ,
и переставим уравнения (1) так, чтобы
матрица выбранного минора оказалась в
левом верхнем углу основной матрицы
системы. Короче говоря, будем считать,
что
,
и переставим уравнения (1) так, чтобы
матрица выбранного минора оказалась в
левом верхнем углу основной матрицы
системы. Короче говоря, будем считать,
что
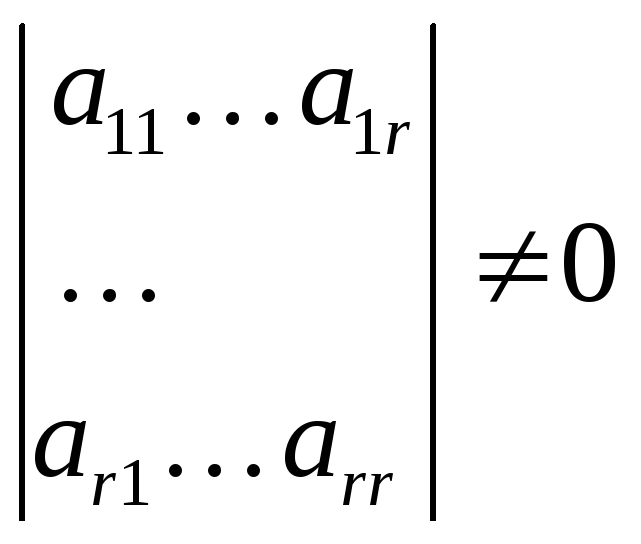 ,
где
,
где
![]() .
В этом предположении рассмотрим наряду
с системой (1) систему
.
В этом предположении рассмотрим наряду
с системой (1) систему
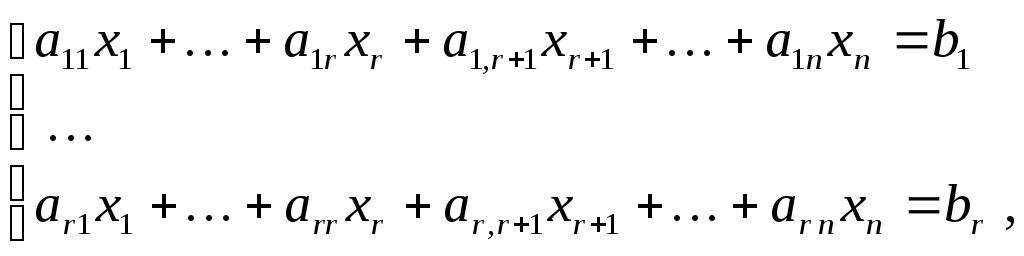 (2)
(2)
состоящую только из первых
![]() уравнений системы (1).
уравнений системы (1).
Теорема 3. Системы (1) и (2) эквивалентны.
Доказательство. Обе системы содержат одинаковое число неизвестных.
1. Если система (1) совместна, то, очевидно, любое ее решение является решением и системы (2) – части системы (1).
2. Докажем, что
если система (2) совместна, то любое ее
решение является решением и системы
(1). В расширенной матрице
![]() системы (1) первые
системы (1) первые
![]() строк базисные. По теореме о базисном
миноре все остальные ее строки суть
линейные комбинации этих базисных
строк. Поэтому в системе (1) каждое
уравнение, начиная с
строк базисные. По теореме о базисном
миноре все остальные ее строки суть
линейные комбинации этих базисных
строк. Поэтому в системе (1) каждое
уравнение, начиная с
![]() -го,
представляет собой линейную комбинацию
первых
-го,
представляет собой линейную комбинацию
первых
![]() уравнений. Следовательно, каждое решение
первых
уравнений. Следовательно, каждое решение
первых
![]() уравнений обращает в тождество все
остальные уравнения.
уравнений обращает в тождество все
остальные уравнения.
3. Если система (2), являющаяся частью системы (1), несовместна, то и вся система (1), очевидно, несовместна.
4. Если система (1) несовместна, то и система (2) несовместна: иначе мы получили бы противоречие с доказанным в пункте 2.
Замечание.
Если
![]() ,
то (1) совпадает с (2) и имеет единственное
решение как система с квадратной
невырожденной матрицей (см. теорему 2).
Если
,
то (1) совпадает с (2) и имеет единственное
решение как система с квадратной
невырожденной матрицей (см. теорему 2).
Если
![]() ,
то назовем
,
то назовем
![]() главными неизвестными, а
главными неизвестными, а
![]() – свободными неизвестными. Запишем
в этом случае систему (2) в виде
– свободными неизвестными. Запишем
в этом случае систему (2) в виде
 .
.
Придадим
свободным неизвестным
![]() произвольные значения
произвольные значения
![]() .
Тогда относительно
.
Тогда относительно
![]() получим систему уравнений
получим систему уравнений
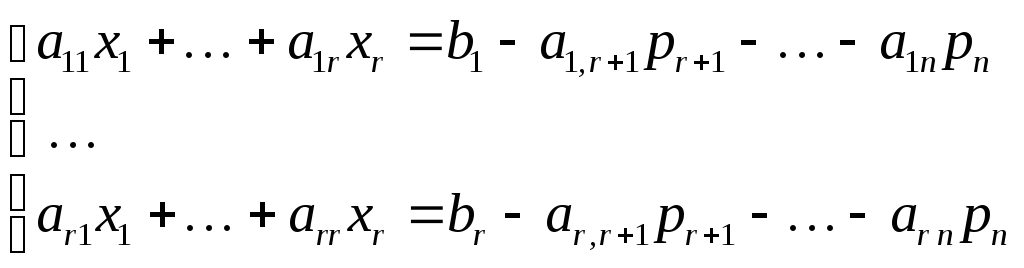 (3)
(3)
с квадратной
невырожденной матрицей. Система (3) имеет
единственное решение
![]() .
Ясно, что
.
Ясно, что
![]() является решением системы (2), а в силу
теоремы 3 – и решением системы (1). Как
видно, в случае
является решением системы (2), а в силу
теоремы 3 – и решением системы (1). Как
видно, в случае
![]() обе системы имеют бесконечно много
решений:
обе системы имеют бесконечно много
решений:
![]() можно выбрать произвольно.
можно выбрать произвольно.
Легко видеть,
что все решения системы (2) получаются
из (3) при некоторых
![]() .
Действительно, если
.
Действительно, если
![]() – решение (2), то взяв в качестве значений
свободных неизвестных именно компоненты
этого решения
– решение (2), то взяв в качестве значений
свободных неизвестных именно компоненты
этого решения
![]() ,
мы получим из (3)
,
мы получим из (3)
![]() в силу однозначной разрешимости
системы (3).
в силу однозначной разрешимости
системы (3).
Итак, в случае
![]()
![]() множество
множество
![]() всех решений системы (1) содержит
всех решений системы (1) содержит
![]() произвольно меняющихся свободных
неизвестных. При любом выборе значений
этих свободных неизвестных значения
остальных
произвольно меняющихся свободных
неизвестных. При любом выборе значений
этих свободных неизвестных значения
остальных
![]() неизвестных определяются однозначно.
Множество
неизвестных определяются однозначно.
Множество
![]() всех решений системы (1) является
всех решений системы (1) является
![]() -параметрическим
семейством и содержит все частные
решения системы (1). Такое множество
называется общим решением системы
(1).
-параметрическим
семейством и содержит все частные
решения системы (1). Такое множество
называется общим решением системы
(1).
Следствие.
Система уравнений (1) с
![]() неизвестными имеет единственное
решение в том и только в том случае, если
неизвестными имеет единственное
решение в том и только в том случае, если
![]()
![]() .
(Докажите самостоятельно.)
.
(Докажите самостоятельно.)
Система уравнений
![]() называется однородной
называется однородной
![]() .
Она совместна:
.
Она совместна:
![]() – тривиальное решение. (Решение
– тривиальное решение. (Решение
![]() называют нетривиальным.)
называют нетривиальным.)
Теорема
4. Однородная система
![]() с
с
![]() неизвестными имеет нетривиальное
решение в том и только в том случае, если
неизвестными имеет нетривиальное
решение в том и только в том случае, если
![]() .
(Докажите самостоятельно.)
.
(Докажите самостоятельно.)
Теорема
5. Однородная система
![]() с квадратной матрицей имеет нетривиальное
решение в том и только в том случае, если
с квадратной матрицей имеет нетривиальное
решение в том и только в том случае, если
![]() .
(Докажите самостоятельно.)
.
(Докажите самостоятельно.)
