Контрольное задание
Задача 1. На заданном множестве точек плоскости Q определены предикаты P1(x), P2(x), P(x). Областью истинности предиката P1(x) является множество Р1, областью истинности предиката P2(x) – множество Р2, областью истинности предиката Р(х) – множество Р, заштрихованная часть области Q.
a) Используя операции над множествами, записать формулу получения множества Р.
б) Используя логические операции, записать формулу предиката P(x).
|
|
|
|
Вариант 1 |
Вариант 2 |
|
|
|
|
Вариант 3 |
Вариант 4 |
|
|
|
|
Вариант 5 |
Вариант 6 |
|
|
|
|
Вариант 7 |
Вариант 8 |
|
|
|
|
Вариант 9 |
Вариант 10 |
Задача 2. Дано множество M={a, b}. Предикат P(x,y), где x M, y M, задан следующей таблицей.
|
x |
y |
P(x,y) |
|
a |
a |
0 |
|
a |
b |
1 |
|
b |
a |
1 |
|
b |
b |
1 |
Определить значение истинности высказывания (с объяснением)
|
Вариант 1 |
x P(x, a) |
Вариант 6 |
y x P(x, y) |
|
Вариант 2 |
x P(x, a) |
Вариант 7 |
x y P(x, y) |
|
Вариант 3 |
y P(a, y) |
Вариант 8 |
y x P(x, y) |
|
Вариант 4 |
y P(a, y) |
Вариант 9 |
x y P(x, y) |
|
Вариант 5 |
x y P(x, y) |
Вариант 10 |
x y P(x, y) |
Задача 3. Выписать все элементы
отношений
и
.
Исследовать свойства отношения
и представить его в виде ориентированного
графа и координатной диаграммы.
|
Вариант 1 |
X = {2, 4, 6, 8}, R = {<x, y>: x < y} |
|
Вариант 2 |
X = {1, 3, 5, 7}, R = {<x, y>: x > y} |
|
Вариант 3 |
X = {2, 5, 7, 9}, R = {<х, y>: (x*y) делится на 2} |
|
Вариант 4 |
X = {1, 4, 9, 22}, R = {<x, y>: (x+y) больше 12} |
|
Вариант 5 |
X = {2, 4, 8, 10}, R = {<x, y>: x y} |
|
Вариант 6 |
X = {3, 6, 9, 15}, R ={<x, y>: y/x нечетно} |
|
Вариант 7 |
X = {2, 4, 16, 22}, R = {<x, y>: (x+y) делится на 6} |
|
Вариант 8 |
X = {2, 4, 16, 22}, R = {<x, y>: x / y четно} |
|
Вариант 9 |
X = {2, 4, 8, 10}, R = {<x, y>: (x – y) делится на 3} |
|
Вариант 10 |
X = {3, 6, 9, 11}, R = {<х, y>: (x*y) меньше 55 } |
Задача 4. Решить задачу
|
Вариант 1 |
В классе изучают 10 предметов. В понедельник 6 уроков, причем все уроки различные. Сколькими способами можно составить расписание на понедельник? |
|
Вариант 2 |
Сколько имеется пятизначных чисел, которые делятся на 5? |
|
Вариант 3 |
В роте имеется 3 офицера и 40 солдат. Сколькими способами может быть выделен наряд, состоящий из 1 офицера и 3 солдат? |
|
Вариант 4 |
Сколько способов можно использовать при разложении в 2 кармана 9 монет различного достоинства? |
|
Вариант 5 |
Сколько возможно вариантов при посадке за круглый стол n мужчин и n женщин так, чтобы никакие два лица одного пола не сидели рядом? |
|
Вариант 6 |
Сколько способов можно использовать при выборе 6 карт из колоды, содержащей 52 карты, так, чтобы среди них были карты каждой масти? |
|
Вариант 7 |
В некотором царстве каждые 2 человека отличаются набором зубов. Какова может быть численность населения царства (максимальное количество зубов у человека – 32)? |
|
Вариант 8 |
На рояле 88 клавиш. Сколько существует последовательностей из 6 попарно различных звуков? (В последовательности звуки идут один за другим.) Сколько существует аккордов 6 попарно различных звуков? (Аккорд получается, если 6 клавиш нажаты одновременно.) |
|
Вариант 9 |
Пассажир оставил вещи в автоматической камере хранения, а когда пришел получать вещи, выяснилось, что он забыл номер. Он только помнит, что в номере были числа 23 и 37. Чтобы открыть камеру, нужно правильно набрать пятизначный номер. Какое наибольшее количество номеров нужно перебрать, чтобы открыть камеру? |
|
Вариант 10 |
У англичан принято давать детям несколько имен. Сколькими способами можно назвать ребенка, если ему дадут не более 3 имен, а общее число имен равно 300? |
Задача 5. Для орграфа, представленного следующей матрицей инциденций, найти матрицу смежности, нарисовать диаграмму графа и определить будет ли он связным, сильно связным или несвязным.
|
- 0 -1 0 0 0 0 -1 1 1 0 0 0 0 0 0 0 1 -1 0 0 0 0 0 0 0 0 -1 1 0 0 0 1 1 1 0
|
- 1 -1 0 0 0 -1 0 -1 0 1 -1 0 0 0 0 0 0 0 1 -1 0 0 1 1 0 0 0 1 -1 0 0 0 0 0 0 0 1 1 0 0 |
|
Вариант 1 |
Вариант 2 |
|
-1 1 0 0 0 1 0 1 0 -1 1 0 0 0 0 0 0 0 -1 1 0 0 -1 -1 0 0 0 -1 1 0 0 0 0 0 0 0 -1 -1 0 0 |
-1 1 0 0 0 0 0 0 0 -1 1 0 0 0 1 -1 0 0 -1 1 0 1 0 0 0 0 0 -1 1 0 0 0 0 0 0 0 -1 -1 -1 0 |
|
Вариант 3 |
Вариант 4
|
|
- 1 -1 0 0 0 0 0 0 0 1 -1 0 0 0 -1 1 0 0 1 -1 0 -1 0 0 0 0 0 1 -1 0 0 0 0 0 0 0 1 1 1 0 |
|
|
Вариант 5 |
|
1 0 -1 0 -1 0 0 
1 0 0 0 0 0 -1 0 
1 0 0 0 0 0 1 0 
1 0 0 0 0 0 0 1 
1 0 0 0 0 0 0 -1 Для орграфа, представленного следующей матрицей смежности, найти матрицу инциденций, нарисовать диаграмму графа и определить будет ли он связным, сильно связным или несвязным.
|
0 1 0 1 0 0 1 1 0 1 0 1 0 1 0 0 1 0 0 0 0 |
0 1 0 1 1 0 0 1 0 0 1 1 1 0 0 0 0 0 1 0 0 |
|
Вариант 6 |
Вариант 7 |
|
0 1 0 0 0 0 1 0 0 1 1 0 0 1 0 0 0 0 1 0 0 |
0 1 0 0 1 1 1 0 0 0 1 1 1 0 0 1 1 1 1 1 0 |
|
Вариант 8 |
Вариант 9 |
|
0 1 1 1 0 1 0 0 0 1 1 0 0 1 0 1 0 1 0 1 0 1 0 1 0 |
|
|
Вариант 10 |
|
1 1 1 1
1 0 1 0
1 1 0 0
1 1 1 1
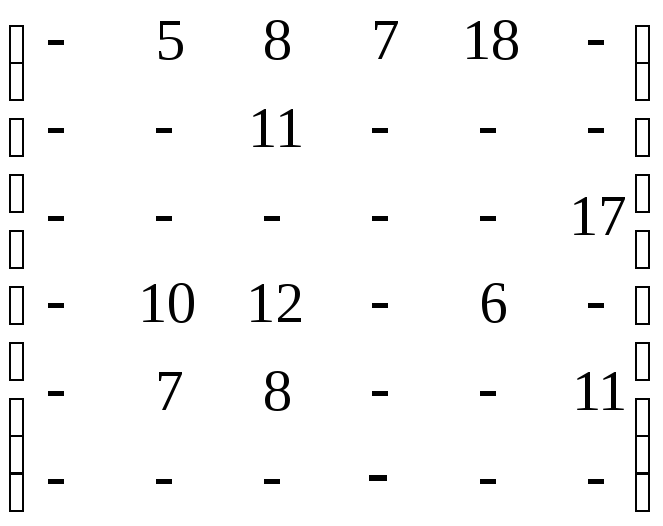
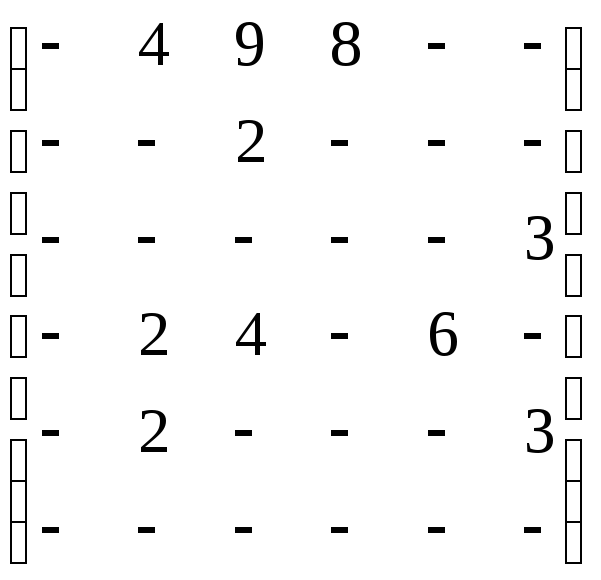
Задача 5. По заданной матрице расстояний графа G найти величину минимального пути и сам путь от вершины s=х1 до вершины t=х6, а затем величину максимального пути и сам путь между теми же вершинами.
|
|
|
|
Вариант 1 |
Вариант 2 |
|
|
|
|
Вариант 3 |
Вариант 4 |
|
|
|
|
Вариант 5 |
Вариант 6 |
|
|
|
|
Вариант 7 |
Вариант 8 |
|
|
|
|
Вариант 9 |
Вариант 10 |
