лабораторная работа / Определение устойчивости системы по критерию Шур-Кона / ТАУ - Лаба _3

Пусть дана схема системы:

Рисунок 1 – Первоначальная структурная схема системы

Значения передаточных функций каждого из элементов выглядят следующим образом:

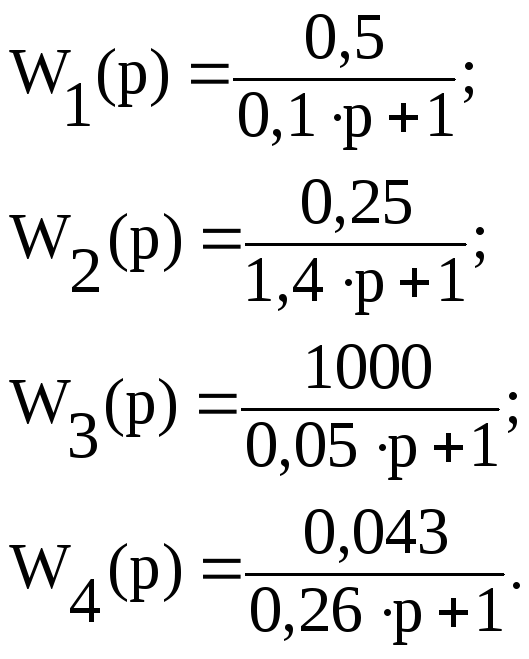
Применяя правила преобразования структурных схем, упростим данную схему системы.

Преобразуем в схеме последовательно стоящие элементы:

Рисунок 2 – Преобразованная схема системы

Преобразуем схему с учетом обратной связи:

Используя программу MathCAD, подставив значения функций, получим выражение общей передаточной функции:

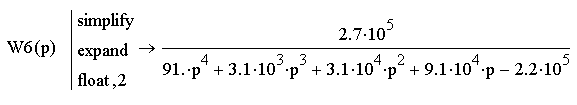
Разобьем общую передаточную функцию на простейшие дроби:

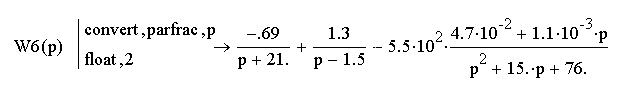
Проведем z-преобразование. Для импульсных систем характерно построение решетчатых функций. Для решетчатых функций времени может быть введено понятие дискретного преобразования Лапласа. Для исследования импульсных систем большое распространение получило так называемое z-преобразование, которое связано с дискретным преобразование Лапласа и вытекает из него.

С помощью программы MathCad проведем обратное преобразование Лапласа:

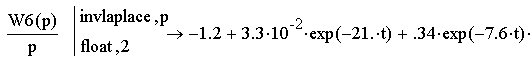
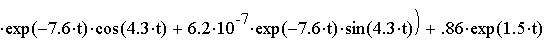
Проведем z-преобразование с помощью функции ztrans прикладной программы MathCAD:

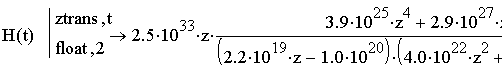
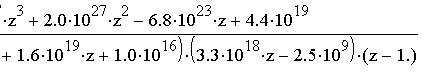
Проведя обратное преобразование Лапласа, найдем значение переходной функции системы:

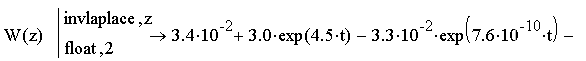
Построим график переходного процесса системы:

Рисунок 3 – График переходного процесса системы

Определим устойчивость системы по критерию Шур-Кона.

Алгебраический критерий Шур-Кона по характеристическому уравнению замкнутой системы позволяет судить о расположении корней на плоскости z. Корни характеристического уравнения будут лежать внутри единичной окружности, что указывает на устойчивость системы, если коэффициенты уравнения удовлетворяют следующим условиям:

Упростив выражение W(z), получаем:

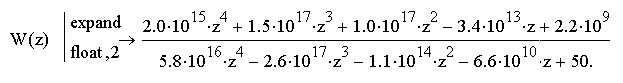
В нашем случае характеристическое уравнение имеет следующий вид:

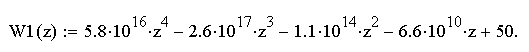
Запишем коэффициенты определителя Шур-Кона:

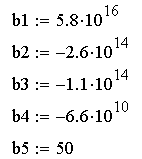
Подсчитаем миноры определителя Шур-Кона:

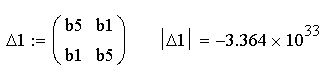
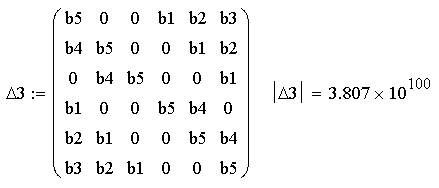
Вывод: после преобразования структурной схемы системы и проведе- ния z-преобразования, было получено значение передаточной функции систе-мы и построен график переходного процесса, по которому видно, что данная система не является устойчивой. Также было проведено определение устой-чивости системы по критерию Шур-Кона, которое тоже показало, что система является неустойчивой, так как третий минор определителя Шур-Кона положи-телен, а по условию устойчивости должен быть отрицательным.