Индивидуальное задание 5 Численные методы решения задачи Коши для обыкновенных дифференциальных уравнений

Цель задания - закрепление теоретического материала, составление алгоритмов и программ для решения систем дифференциальных уравнений первого порядка, удовлетворяющих начальным условиям.

Варианты индивидуальных заданий приведены в табл. 5-7

Порядок выполнения задания

1. Составить головную программу, содержащую обращение к подпрограммам EYLER, RGK.

2. Составить подпрограмму вычисления правых частей уравнений системы.

3. Произвести вычисления на ЭВМ.

4. Произвести анализ полученных результатов.

5. Оформить отчет и представить его к защите.

42

Таблица 5

Варианты индивидуального задания 5

а)

Номер варианта	f ( x; y1, y2)	a	y20
1 2 3 4 5 6	-a0.8x	0.01 0.02 0.03 0.07 0.09 0.05	0.05 1/3 0.25 0.2 1/6 1/9
7 8 9 10	-axy2-y1	0.01 0.02 0.03 0.04	0.5 0.33 0.25 0.2
11 12 13 14	-ay1e-x	0.01 0.02 0.05 0.06	0.5 1/3 0.25 0.2
15 16 17	-0.04e-1.2x	- - -	0.2 0.3 0.4
18	-0.04e0.8	-	0.2
19 20 21 22	-axy2-x2y1		0.2 1/6 1/7 0.125

б)привести к системе дифференциальных уравнений путем введения дополнительных переменных

y®y(1) , y’®(2) , y” ®y(3) и т.д.

45

Таблица 6.

Номер варианта	Дифференциальное уравнение	Интервал [а;b]	x0	y0	y0’	Шаг h
23	y”=3y’-2y+2x-3	0; 0.3	0	1	0	0.1
24	y”+4y’+4y=0	0; 0.5	0	1	-1	0.05
25	y”+yy’-6y=2x2-x	0; 0.6	0	-1	1	0.1
26	y”+2y’+2y=2e-xcosx	0; 1	0	1	0	0.1
27	(1+x2)y”+(y’)2+1=0	1; 2	1	1	-1	0.1
28	y”+4y=sinx+sin2x	0; 1	0	1	-0.5	0.1
29	y(3)=y”-y’+1	0; 2	0	1	0	0.4

в)

Таблица 7

Номер варианта	f1 ( x; y1; y2 )	f2 ( x; y1; y2)	Интервал [а;b]	x0	y10	y20	Шаг h
30	y1+y2+x	-4y1+3y2+2x	0; 0.3	0	1	0	0.05

Краткие сведения из теории и основные алгоритмы .

Определение 1. Дифференциальное уравнение - уравнение, содержащее неизвестную функцию одного или нескольких переменных , независимые переменные и производные неизвестной функции по независимым переменным.

Примеры:

- неизвестная функция (1)

- неизвестная функция (2)

неизвестная функция (3)

46

Определение 2. обыкновенным дифференциальным уравнением порядка r называется уравнение (относительно неизвестной функции y одного независимого х ) вида :

F (x, y(x), y'(x), ... y^(r)(x)) = 0 (4)

где r - порядок наивысшей производной, входящей в уравнение.

Определение 3.Если уравнение линейно по y, y', .. y^{( r )} , то оно называется линейным .

Определение 4.Под дифференциальным уравнением в явной форме понимают дифференциальное уравнение , разрешенное относительно старшей производной:

y^(r) (x) = f (x, y(x), y'(x), ... y^(r-1)(x)) (5)

Определение 5.Уравнение (4) называется уравнением в неявной форме. Решить дифференциальное уравнение - это значит найти все неизвестные функции, обращающее уравнение в тождество. В общем случае неизвестные функции определяются дифференциальным уравнением неоднозначно (если решение вообще существует), поэтому на искомые функции часто накладываются дополни тельные условия.

Под интегрированием уравнения (4) понимают нахождение функции y(x),которая удовлетворяет этому уравнению. При этом y(x) называется решением дифференциального уравнения.

Общее решение обыкновенного дифференциального уравнения порядка r имеет вид

y = y ( x; C ₁ ... C_r) ,

где C1...Cr - произвольные постоянные. При любом наборе конкретных постоянных получаются частные решения.

Задача Коши (задача с начальными условиями) есть задача о нахождении частного решения,

которого удовлетворяет r начальным условиям

y(x₀)=y₀ y'(x₀)=y₀',...y^(r-1) (x₀)=y₀^(r-1)

Если известно общее решение , то для решения задачи Коши постоянные находят из уравнений

y(x; C₁ ... C_r ) = y₀

47

Определение 6.Графическое изображение частного решения называют интегральной кривой

Общее решение дифференциального уравнения r-го порядка определяет r-параметрическое семейство интегральных кривых. Обратно, каждое r-параметрическое семейство определяет (при некоторых дополнительных условиях) дифференциальное уравнение r-го порядка, которое получается путем исключения постоянных C1...Cr из уравнений

___

y⁽ⁱ⁾ (x) = y⁽ⁱ⁾ (x; C1 ... Cr ) ( i = 0, r )

Таким образом дифференциальное уравнение описывает семейство кривых.

Пример:

Семейство всех окружностей на плоскости ( x - C₁ )² + ( y-C₂ )² = C₃² содержит три параметра. Трехкратное дифференцирование приводит к уравнениям

x - C₁ + ( y - C₂ ) y' = 0

1 + ( y - C₂ ) y'' + ( y' )² = 0

( y - C₂ ) y'''+ 3y'y'' = 0

Исключая С₂ из двух последних уравнений, получаем

y'''( 1 + (y')² ) - 3y' ( y'')² = 0

Дифференциальное уравнение в явной форме имеет вид:

y'= f(x,y)

Если через точку М(x,y) проходит график решения y=y(x) уравнения y'= f(x,y), то наклон & касательной к графику в точке М(x,y) определяется непосредственно из уравнения

tg a = y'(x) = f(x,y)

Таким образом дифференциальное уравнение в каждой точке рассматриваемой области задает направление касательной к кривой решения. Через каждую точку проходит единственная интегральная кривая.

Любое дифференциальное уравнение n - порядка, которое можно разрешить относительно старшей производной, легко сводится из n уравнений первого порядка путем введения новых переменных.

y⁽ⁿ⁾ = f( x; y', y'', ... , y^(n-1) )

y₁ = y

y₂ = y'

y₃ = y'' (6)

. . .

y_n = y^(n-1)

48

тогда

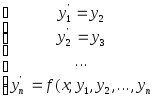(7)

Численное решение задачи Коши состоит в построении таблицы приближенных значений y₁, y₂, ... , y_m решения уравнения в точках (узлах) сетки:

x_i = x₀ + ih, i = 1, 2 ... , M ; x₀ = a, x_m = b ;

h - шаг интегрирования