2. Метод Гаусса с выбором главного элемента в строке.

Hа каждом i-м шаге выбирается элемент, равный max|a_ij|. Пусть это будет элемент a_iL. Переобозначаем неизвестные: x_L = x_i, ax_i = x_L, т.е. переставляем L и i столбцы матрицы , а далее производим i-й шаг метода Гаусса.

Блок-схема алгоритма приведена на рис. 3.

М - массив индексов неизвестных ; К - номер столбца, содержащего max элемент; R - рабочая переменная , используемая для перестановки элементов столбцов матрицы коэффициентов, а также для переобозначения индексов неизвестных (элементы массива М меняются местами).

Индивидуальное задание 2.

Численные методы определения интегралов.

Цель - закрепление теоретического материала, составление алгоритмов и программ для приближенного вычисления определенных интегралов с заданной точностью.

Варианты индивидуальных заданий приведены в табл.2.

Порядок выполнения задания.

1. Представить геометрическую интерпретацию метода.

2. Составить алгоритм вычисления определенного интеграла, используя предложенный вам численный метод.

3. Составить программу на алгоритмическом языке.

4. Ввести программу в ЭВМ и получить результаты.

5. Оформить отчет и представить его к защите.

Варианты индивидуального задания 2.

Таблица 2

№ п/п	Подынтегральная функция	Границы интегриро-вания	Формула Ньютона-Лей-бница	Точность вычисления	Нача-льное число разбие-ния	Метод вычис-ления
1	2	3	4	5	6	7
1		[ 2 , 5 ]	-	10-4	10	Симсо-на
2		[ 0 , 2 ]	1/4 ln(a4+x4)	10-3	10	Симсо-на

13

Продолжение таблицы 2

1	2	3	4	5	6	7
31		[ 0 , 2 ]	-	5	20	Трапеций и прямо- угольников
42		[ 0 , x ], xÎ[0,1], шаг 0,25	-	-	30	Симпсона
52		[ 0 , x ], xÎ[0,2], шаг 0,25	-	-	50	Трапеций
62		[ 0 , x ], xÎ[0,1], шаг 0,25	-	10-4	20	Симпсона
7		[-p/3,-p/4]	x-1/a*tg(ax/2)	10-3	20	Симпсона
8	x cos(ax), a=2.5	[0, p/3]	-	10-4	10	Симпсона
9		[ 0 , 3 ]				Трапеций
10		[ 1 , 5 ]		10-5	20	Прямоугольников
11		[ 1 , 5 ]		10-4	30	Симпсона
12		[ 1 , 2 ]		10-5	50	Трапеций
13	cos2(ax),a=1,15	[-p/4,p/4]		10-3	30	Симпсона
14		[ 0 , 6 ]		10-4	20	Симпсона
152	(x-5)2(10-x)	[ 0 , 20 ]	-	10-5	10	Трапеций и прямо- угольников
16		[ -1 , 2 ]	-	5,10-5	10	Трапеций и прямо- угольников
17		[ 0 , 5 ]	-	4	10	Трапеций и Симпсона

15

1	2	3	4	5	6	7
18		[1,3]	-0.25 ln(a4-x4)	10-3	10	Симпсона
19*	esin2(x) sin(3x)	[0,p]	-	10-4	10	Симпсона; m-?
20		[0.1, p /2]	-	10-4	20	Прямо- угольников, трапеций
21		[0,1]	-	10-3	20	Прямо-угольников, трапеций, Симпсона
22		[-1,1]		10-4	10	Симпсона
23		[0,2]		10-3	10	Симпсона
24	ecos(x)cos(2x)	[0, p]	-	10-4	6	Симпсона
25	cos2(2x)	[-2,2]	-	10-4	10	Симпсона
26		[-1,1]	-	10-4	10	Прямо-угольников, трапеций
27	a2 - x2 a=15.36	[1,5]		10-4	30	Трапеций
28		[1,3]		10-3	50	Прямо-угольников
29		[1,4]		10-4	40	Симпсона
303		[2,5]		10-4	20	Симпсона

16

Примечания:

1. Сравнить результат, полученный по формуле трапеций и по формуле прямоугольников за 5 итераций (на каждой итерации число разбиений увеличивается вдвое).

2. Построим таблицу функции F(x) на указанном отрезке с указанным шагом.

3. Сравнить результат, полученный по формуле Симпсона и по формуле Ньютона-Лейбница, если за 5 иттераций заданная точность достигнута не будет, то вывести на печать соответствующее сообщение.

Замечания:

1. Во всех вариантах, в которых указана формула Ньютона-Лейбница, производятся вычисления по данной формуле и результат сравнивается с величиной, полученной с использованием приближенных методов вычисления определенных интегинтегралов.

2. Результаты выводятся на печать с соответствующими комментариями.

Краткие сведения из теории и основные алгоритмы

Определение.

Определенный интеграл с пределами интегрирования a и b можно представить как площадь фигуры, ограниченной ординатами а и b, осью абсцисс x и графиком подынтегральной функции ¦(x) (рис.4)

Рис. 4.

Обыкновенный интеграл, у которого известна его первообразная

F(x)(F'(x) = ¦(x))

вычисляется по формуле Ньютона-Лейбница

I = F(b) - F(a)

поэтому достаточно вычислить значение функции F(x)

17

Численное интегрирование применяется, если нахождение F(x) сложно или невозможно. Оно заключается в интерполяции ¦(x) на отрезке [a,b] подходящим полиномом, для которого определенный интеграл вычисляется по формулам численного интегрирования. Обычно отрезок [a,b] разбивается на m частей , к каждой из которых применяется соответствующая простая формула.Таким образом получают составные формулы численного интегрирования.

1. Метод прямоугольников

Метод прямоугольников - простейший прием численного интегрирования, при котором функция ¦(x) заменяется интерполяционным многочленом нулевого порядка.

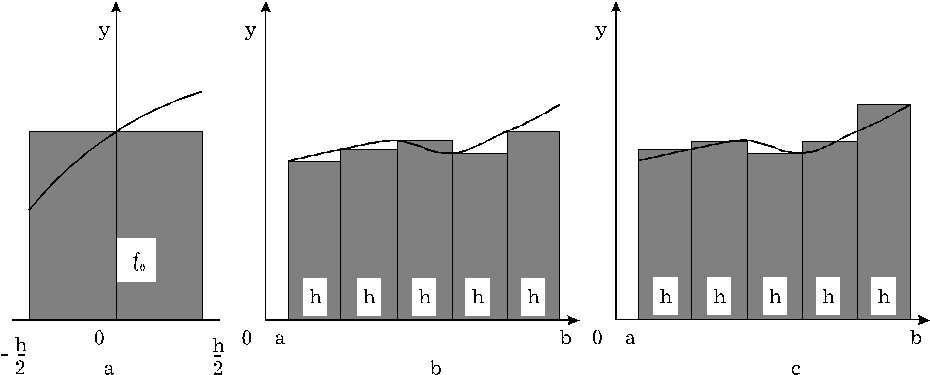
Рис. 5.

Функцию ¦(x) на интервале [-h/2,h/2] (рис.5,а) можно заменить на ¦₀=const, тогда

Это и есть формула прямоугольников , т.е. S₁ = ¦₀* h

Для повышения точности интегрирования отрезок [a,b] разбивается на m частей и формула прямоугольников применяется к каждому отрезку, на котором значение функции ¦(x) заменяется константой.

формула левых прямоугольников

(рис.5,в)

18

формула правых прямоугольников

(рис.5,с)

2. Метод трапеций

Метод трапеций заключается в замене функции ¦(x) на интервале [a,b] интерполяционным многочленом первого порядка (линейная интерполяция),рис.6,а

рис.6

Функцию ¦(x) на интервале [0,h] можно заменить интерполяционным многочленом первой степени в форме Лагранжа или Ньютона:

¦(x)»¦₀+(¦₁-¦₀)*x/h

тогда

а это и есть площадь прямоугольников

Для повышения точности интерполирования отрезок [a,b] разбивается на m частей и формула трапеций применяется к каждому отрезку, на котором значение функции f(x) заменяется интерполяционным многочленом первой степени (рис.6,в)

19

3. Метод парабол (Симпсона)

Метод парабол заключается в замене функции ¦(x) на интервале [a,b] интерполяционным многочленом второго порядка (квадратичная интерполяция).(рис 7 а).Парабола проходит через точки с координатами (-h , ¦_-1) ; (0, ¦₀) ; (h, ¦₁).

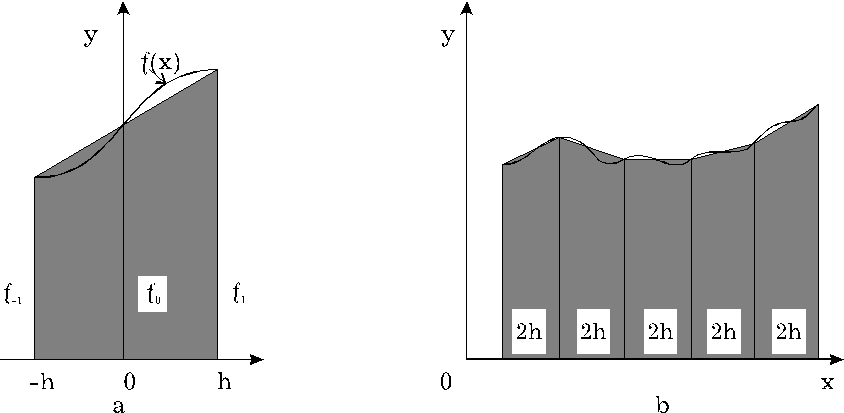
рис. 7

(после раскрытия скобок и приведения подобных)

формула парабол

Для повышения точности интегрирования отрезок [a,b] разбивается на 2m частей и формула парабол применяется к каждому отрезку [x_2f,x_2f+2], на котором значение функции f(x) заменяется интерполяционным многочленом второй степени (рис. 7, в)

20

Просуммируем по всем интервалам

Формулу Симпсона можно записать в виде

обозначив N=2m, имеем

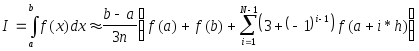
Блок-схемы алгоритмов приведены на рис.8.

Рекомендации. Алгоритм вычисления подынтегральной функции оформить либо в виде процедуры FUNCTION, либо оператором определения функции пользователя.

Индивидуальное задание 3