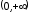Применение теории max и min в решении задач

С помощью теории max и min можно решать задачи механики, физики, геометрии, в которых требуется найти минимальное или максимальное значение функции.

Задача. Какое положительное число, будучи сложенное с обратным ему числом дает наименьшую сумму?

Решение.

Обозначим за x неизвестное число, тогда обратное ему число – 1/x.

Надо найти 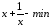. ОДЗ:

Так как , то – искомое число.

Тогда .

Выполним проверку, действительно ли в точке минимум.

X		-1		0		1
	+	0	–	Ø	–	0	+
		max				min

Выпуклость графика функции. Точки перегиба

Определение. Функция называется выпуклой вверх или просто выпуклой, если все точки кривой расположены ниже любой ее касательной.

Определение. Функция называется выпуклой вниз или просто вогнутой, если все ее точки расположены выше любой касательной, проведенной к графику.

y y

0 x 0 x

Теорема. Если функция во всех точках интервала имеет отрицательную вторую производную, то есть , то функция выпукла на этом интервале. Если же , , то функция вогнутая.

Определение. Точки, в которых выпуклая часть отделяется от вогнутой, называются точками перегиба.

Теорема. В точках перегиба вторая производная обращается в нуль или не существует.

Пример.

Исследуйте на выпуклость, вогнутость и точки перегиба функцию .

x = 0 – точка перегиба.

X		0
	–	0	+

Теорема. Если функция имеет вторую, третью, … (n-1)-ую производную в точке x = x₀ равную нулю и у этой функции будет существовать n-ая производная, которая не равна нулю в точке x = x₀, то

1. если n – нечетное, то x = x₀ – точка перегиба;

2. если n – четное, то x = x₀ – точка экстремума, а именно точка максимума, если ; точка минимума, если .

Контрольные вопросы:

1. Приведите пример нечетной функции.

2. Приведите пример функции возрастающей на интервале .

3. Приведите пример окрестности точки .

4. Будет ли точка – точкой экстремума, если ?

5. Какая функция называется вогнутой, а какая выпуклой?

6. Будет ли прямая асимптотой графика функции ?

Схема исследования функции и построения графика с помощью производных

Основные вопросы:

1. Схема исследования функции.

2. Пример исследования функции и построения графика.

СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ И ПОСТРОЕНИЯ ГРАФИКА С ПОМОЩЬЮ ПРОИЗВОДНЫХ

Исследование функции целесообразно вести в определенной последовательности.