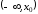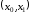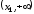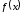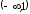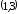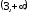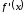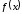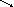- •Исследование функций при помощи производных
- •Условие постоянства функции
- •Четность и нечентность функции
- •Асимптоты
- •Условия монотонности функции
- •Максимум и минимум функции
- •Наибольшее и наименьшее значения функции на отрезке
- •Применение теории max и min в решении задач
- •Выпуклость графика функции. Точки перегиба
- •Асимптоты.
- •4. Асимптоты.
- •Формула Тейлора для произвольной функции
- •Разложения по формуле Маклорена некоторых элементарных функций:
Максимум и минимум функции
Определение.
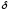 -окрестностью
точки
-окрестностью
точки
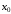 называется интервал (x0–δ,
x0+δ),
где
называется интервал (x0–δ,
x0+δ),
где
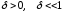 .
.
Определение.
Точка
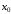 называется точкой максимума (
называется точкой максимума (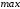 )
функции f(x),
если существует такая
)
функции f(x),
если существует такая
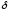 -окрестность
точки
-окрестность
точки
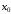 ,
что для всех
,
что для всех
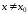 из этой окрестности выполняется
неравенство:
из этой окрестности выполняется
неравенство:
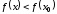 .
.
Определение.
Точка
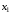 называется точкой минимума (
называется точкой минимума (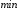 )
функции f(x),
если существует такая
)
функции f(x),
если существует такая
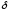 -окрестность
точки
-окрестность
точки
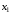 ,
что для всех
,
что для всех
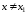 из этой окрестности
из этой окрестности
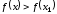 .
.
y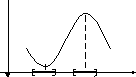
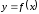

min max x0–δ x0 x0+δ x
0 x1 x0 x
Определение. Минимум и максимум функции называется экстремумом функции.
Теорема (Необходимые
условия экстремума).
Если дифференцируемая функция
 имеет экстремум в точке
имеет экстремум в точке
 ,
то ее производная в этой точке равна
нулю, то есть
,
то ее производная в этой точке равна
нулю, то есть
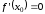 .
.
Замечание.
Обратная теорема неверна, то есть если
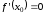 ,
то это не значит, что
,
то это не значит, что
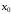 – точка экстремума.
– точка экстремума.
Определение. Точки, в которых производная функции равна нулю или не существует, называются критическими.
Замечание. Таким образом, непрерывная функция может иметь экстремум лишь в критических точках.
Теорема.
Если непрерывная функция
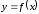 дифференцируема в некоторой
дифференцируема в некоторой
 -окрестности
критической точки x0
и при переходе через нее (слева направо)
производная
-окрестности
критической точки x0
и при переходе через нее (слева направо)
производная
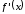 меняет знак с плюса на минус, то x0
– есть точка максимума; с минуса на
плюс, то x1
– точка минимума.
меняет знак с плюса на минус, то x0
– есть точка максимума; с минуса на
плюс, то x1
– точка минимума.
|
x |
|
x0 |
|
x1 |
|
|
|
+ |
0 |
– |
0 |
+ |
|
|
|
max |
|
min |
|
Пример.
Найдите интервалы монотонности и экстремумы функции
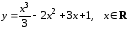 .
.
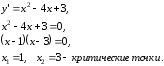
|
x |
|
1 |
|
3 |
|
|
|
+ |
0 |
– |
0 |
+ |
|
|
|
max |
|
min |
|
Точка максимума x = 1, ymax (1)=7/3, А(1,7/3).
Точка минимума x = 3, ymin (3)=1, В(3,1).
На
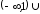
 функция возрастает, на
функция возрастает, на
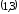 убывает.
убывает.
y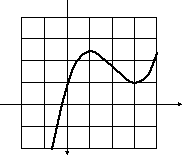
2
1
–1 0 1 3 x
Теорема.
Если в точке
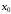 первая производная функции
первая производная функции
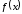 равна нулю, то есть
равна нулю, то есть
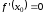 ,
а
,
а
 ,
то при
,
то при
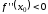 в точке
в точке
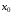 – max,
при
– max,
при
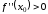 в точке
в точке
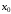 – min.
– min.
Пример.
Исследуйте на экстремумы функцию
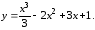
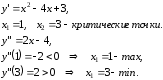
Наибольшее и наименьшее значения функции на отрезке
y
наиб max
max
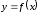
min
min наим
0 a b x
Для различных участков функция имеет различные наибольшие и наименьшие значения.
Правило
нахождения наибольшего и наименьшего
значений функции на
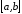 :
:
-
найдите критические точки функции на интервале
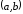 ,
, -
вычислите значения функции в найденных критических точках,
-
вычислите значения функции на концах отрезка, (в точках a и b),
-
среди всех вычисленных значений функции выберите наибольшее и наименьшее.
Пример.
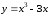 .
Найдите наименьшее и наибольшее значения
на отрезке
.
Найдите наименьшее и наибольшее значения
на отрезке
 .
.
1)
 ,
,
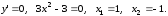
2)
 ,
,
 .
.
3)
 ,
,
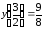 .
.
4)
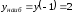 ,
,
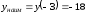 .
.