Исследование функций при помощи производных

Основные вопросы:

1. Четность и нечетность функции.

2. Монотонность функции.

3. Асимптоты.

4. Экстремумы.

5. Наибольшее и наименьшее значения функции на отрезке.

6. Выпуклость графика функции. Точки перегиба.

Условие постоянства функции

Теорема. Пусть функция определена и дифференцируема на некотором интервале . Тогда, для того чтобы функция была постоянна на этом интервале, необходимо и достаточно, чтобы ее производная равнялась нулю.

.

y

с

0 a b x

Четность и нечентность функции

Определение. Функция 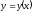называется четной, если .

Определение. Функция называется нечетной, если .

График четной функции симметричен относительно оси ординат, нечетной – относительно начала координат.

Определение. Функция ни четная, ни нечетная называется функцией общего положения.

Асимптоты

Построение графика функции значительно упрощается, если знать его асимптоты.

Определение. Асимптотами графика функции называются прямые, к которым функция неограниченно приближается при увеличении ее в бесконечность.

y y

0 x

0 x

Асимптоты бывают трех видов:

1. вертикальные асимптоты задаются уравнением вида: .

Определение. Прямая является вертикальной асимптотой графика функции , если .

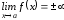• Вертикальная асимптота может возникнуть в точках разрыва 2-го рода.

• На границах области определения, если она ограничена.

y

Пример.

имеет вертикальную асимптоту в точке , 0

так как

Пример. y

. Следовательно, – 0

вертикальная асимптота.

2. Горизонтальные асимптоты задаются уравнением .

Определение. Прямая является горизонтальной асимптотой графика функции , если .

Пример.

.

Следовательно, при график имеет горизонтальную асимптоту .

Следовательно, при 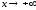горизонтальной асимптоты нет.

3. Наклонные асимптоты имеют уравнение прямой , где .

Замечание.

При наклонная асимптота вырождается в горизонтальную при условии, что .

Если 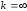, то наклонная асимптота вырождается в вертикальную.

Если , то асимптота проходит через начало координат.

Если , то асимптоты не существует.

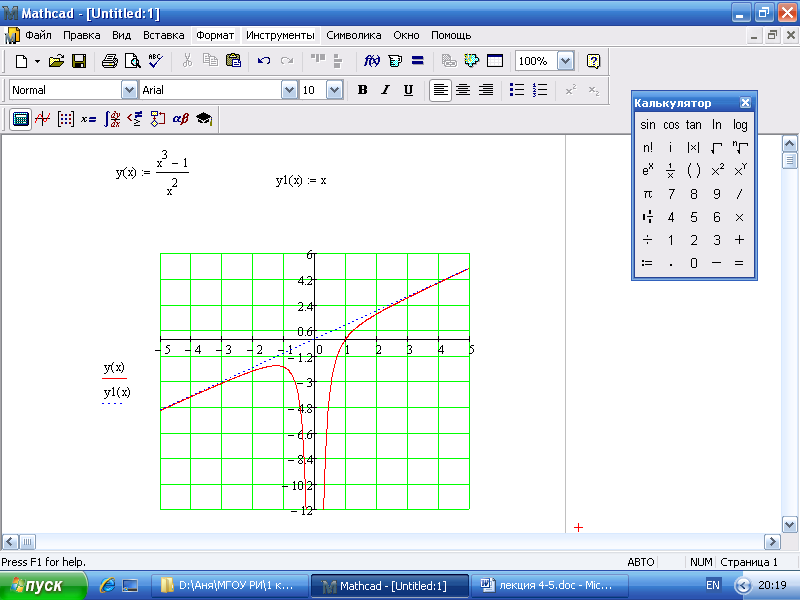
Пример.

Найдите наклонную асимптоту .

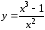Уравнение наклонной асимптоты будет иметь вид , где

То есть – наклонная асимптота.

Условия монотонности функции

Определение. Функция называется возрастающей на интервале , если .

Определение. Функция называется убывающей на интервале , если .

y y

f(x₂) f(x₁)

f(x₁) f(x₂)

0 x₁ x₂ x 0 x₁ x₂ x

Определение. Возрастающие и убывающие функции называются монотонными функциями.

Теорема (Необходимые условия). Если дифференцируемая на интервале функция f(x) возрастает, то , если убывает, то .

Теорема (Достаточные условия). Если функция f(x) дифференцируема на интервале и , то эта функция возрастает (или убывает) на интервале .