
- •Практическое занятие 2. Определители. Вычисление определителей
- •Практическое занятие 3. Вычисление определителей порядка
- •Теоретический диктант.
- •Проверка домашнего задания.
- •Решение типовых задач.
- •Практическое занятие 4. Обратная матрица. Нахождение обратной матрицы с помощью линейных преобразований.
- •Проверка домашнего задания.
- •Решение типовых задач.
- •Проверка домашнего задания.
- •Решение типовых задач.
- •Практическое занятие 6. Матричные уравнения.
- •Проверка домашнего задания.
- •Решение типовых задач.
- •Практическое занятие 7. Подготовка к рубежной аттестации 1.
- •Теоретический диктант.
- •Решение типовых задач.
- •Практическое занятие 10. Решение систем линейных уравнений матричным методом.
- •Проверка домашнего задания.
- •Решение типовых задач.
- •Практическое занятие 11. Решение систем линейных уравнений методом Крамера.
- •Теоретический диктант.
- •Проверка домашнего задания.
- •Решение типовых задач.
- •Практическое занятие 12. Векторы и операции над ними. Линейная комбинация системы векторов.
- •Теоретический диктант.
- •Проверка домашнего задания.
- •Решение типовых задач.
- •Практическое занятие 13. Система векторов и ее линейная зависимость. Базис системы векторов.
- •Теоретический диктант.
- •Проверка домашнего задания.
- •Решение типовых задач.
- •Практическое занятие 14. Базис и ранг системы векторов. Разложение вектора по базису.
- •Проверка домашнего задания.
- •Решение типовых задач.
- •Практическое занятие 15. Однородные системы линейных уравнений. Фундаментальный набор решений.
- •Теоретический диктант.
- •Проверка домашнего задания.
- •Решение типовых задач.
- •Проверка домашнего задания.
ПЛАНЫ
ПРАКТИЧЕСКИХ ЗАНЯТИЙ
ПО ЛИНЕЙНОЙ АЛГЕБРЕ
для студентов 1 курса группы ЭОО 11/1
Практическое занятие 1.
Матрицы и операции над ними.
Контрольные вопросы:
-
Матрица размера
 .
. -
Квадратная матрица
 -го
порядка.
-го
порядка. -
Главная диагональ квадратной матрицы.
-
Побочная диагональ квадратной матрицы.
-
Нулевая матрица.
-
Единичная матрица.
-
Матрица ступенчатого вида.
-
Элементарные преобразования матриц.
-
Сумма матриц.
-
Произведение матрицы на число.
-
Транспонирование матрицы.
-
Произведение матриц.
План занятия.
-
Теоретический диктант.
-
Проверка домашнего задания.
-
Решение типовых задач.
|
Номер задания |
Аудиторная работа |
Домашняя работа |
|
1 |
+ |
- |
|
2 |
+ |
- |
|
3 |
+ |
- |
|
4 |
+ |
- |
|
5 |
1 |
2 |
|
6 |
1 |
2 |
|
7 |
1,5 |
2,3,4 |
|
8 |
2,3 |
1,4,5 |
|
9 |
2,4 |
1,3,5 |
Задание 1 (устно).
Чему равны в матрице A
элементы
![]() ,
,
![]() ,
если
,
если
 ?
?
Задание 2
(устно). Какие элементы в матрице
 составляют главную диагональ, а какие
– побочную?
составляют главную диагональ, а какие
– побочную?
Задание 3
(устно). Укажите, какие из матриц
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() являются диагональными, треугольными,
ступенчатыми?
являются диагональными, треугольными,
ступенчатыми?
Задание 4
(устно). Даны две матрицы
 и
и
![]() .
Какое из соотношений верно?
.
Какое из соотношений верно?
1) A = B; 2) A > B; 3) ![]() ; 4) A = B = E;
; 4) A = B = E;
Задание
5. Даны матрицы
![]() и
и
![]() .
Найти:
.
Найти:
1) матрицы
![]() и
и
![]() ,
если
,
если
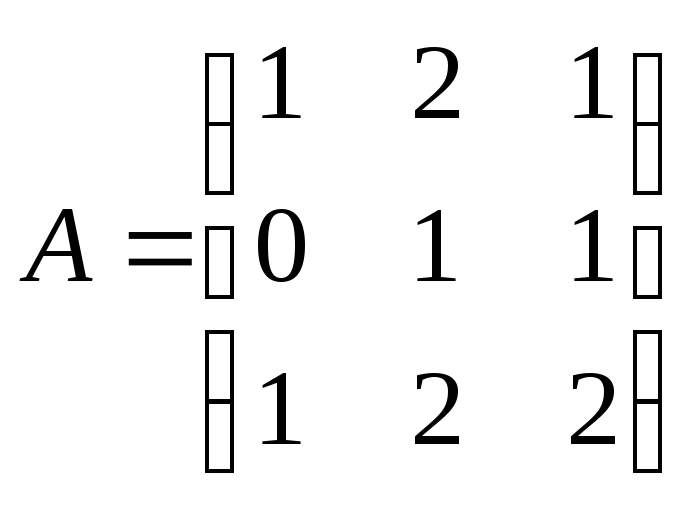 ,
,
 ;
;
2) матрицы
![]() и
и
![]() ,
если
,
если
 ,
,
 .
.
Задание 6. Найдите матрицу X, если:
1)
 ;
;
2)
![]() .
.
Задание 7. Перемножьте матрицы:
1)
 ,
,
![]() ;
;
2)
![]() ,
,
 ;
;
3)
![]() ,
,
 ,
,
 ;
;
4)
 ,
,
 ,
,
![]() ;
;
5)
 ,
,
![]() ,
,
 .
.
Задание 8. Найти
![]() ,
если:
,
если:
1)
![]() ,
,
 ;
;
2)
![]() ,
,
 ;
;
3)
![]() ,
,
 ;
;
4)
![]() ,
,
 ;
;
5)
![]() ,
,
 .
.
Задание 9. Вычислить матричный многочлен:
1)
![]() ,
если
,
если
 ,
,
![]() ,
,
![]() ;
;
2)
![]() ,
если
,
если
![]() ,
,
 ,
,
![]() ,
,
![]() ;
;
3)
![]() ,
если
,
если
 ,
,
 ,
,
 ;
;
4)
![]() ,
если
,
если
![]() ,
,
![]() ,
,
![]() ;
;
5)
![]() ,
если
,
если
![]() ,
,
![]() ,
,
![]() .
.
Практическое занятие 2. Определители. Вычисление определителей
2-го и 3-го порядков.
Контрольные вопросы:
-
Перестановка
 -ой
степени.
-ой
степени. -
Инверсия перестановки.
-
Четная перестановка.
-
Нечетная перестановка.
-
Определитель
 -го
порядка.
-го
порядка. -
Свойства определителей.
-
Вычисление определителя второго порядка.
-
Вычисление определителя третьего порядка (правило Сарриуса).
План занятия.
-
Теоретический диктант.
-
Проверка домашнего задания.
-
Решение типовых задач.
|
Номер задания |
Аудиторная работа |
Домашняя работа |
|
1 |
+ |
|
|
2 |
1,3 |
2,4 |
|
3 |
1,2 |
3,4 |
|
4 |
3,5,6 |
1,2,4 |
|
5 |
1,2,4,5,6 |
3,7,8 |
|
6 |
1 |
2 |
Задание 1 (устно). Как изменится определитель 3-го порядка, если у всех его элементов изменить знак на противоположный?
Задание 2. Определить число инверсий в перестановке:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() .
.
Задание 3. Подберите
![]() и
и
![]() так, чтобы перестановка
так, чтобы перестановка
1)
![]() была нечетной;
была нечетной;
2)
![]() была четной;
была четной;
3)
![]() была четной;
была четной;
4)
![]() была нечетной.
была нечетной.
Задание 4. Входит
ли в определитель
![]() -го
порядка данное произведение. Если да,
то с каким знаком?
-го
порядка данное произведение. Если да,
то с каким знаком?
1)
![]() ,
,
![]() ;
;
2)
![]() ,
,
![]() ;
;
3)
![]() ,
,
![]() ;
;
4)
![]() ,
,
![]() ;
;
5)
![]() ,
,
![]() ;
;
6)
![]() ,
,
![]() .
.
Задание 5. Вычислить определители:
-
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 .
.
Задание 6.
Найдите
![]() из уравнения:
из уравнения:
1)
 ;
;
2)
 ;
;
3)
 .
.
Практическое занятие 3. Вычисление определителей порядка
![]()
Контрольные вопросы:
-
Алгебраическое дополнение элемента определителя.
-
Минор элемента.
-
Разложение определителя по
 -ой
строке.
-ой
строке. -
Разложение определителя по
 -му
столбцу.
-му
столбцу. -
Связь алгебраического дополнения и минора элемента.
-
Вычисление определителей порядка

План занятия.
-
Теоретический диктант.
-
Проверка домашнего задания.
-
Решение типовых задач.
|
Номер задания |
Аудиторная работа |
Домашняя работа |
|
1 |
1,3 |
2 |
|
2 |
2,3 |
1 |
|
3 |
1-3 |
4-6 |
Задание 1. Разложить следующие определители:
-
 по элементам 4-го
столбца;
по элементам 4-го
столбца; -
 по элементам 1-го
столбца;
по элементам 1-го
столбца; -
 по элементам 3-ей
строки.
по элементам 3-ей
строки.
Задание 2 (устно). Как изменится определитель n-го порядка, если:
-
каждый его элемент умножить на -1;
-
его строки записать в обратном порядке;
-
к каждой строке, начиная со 2-ой, прибавить предыдущую.
Задание 3. Вычислить определители:
-
 ;
; -
 ;
; -
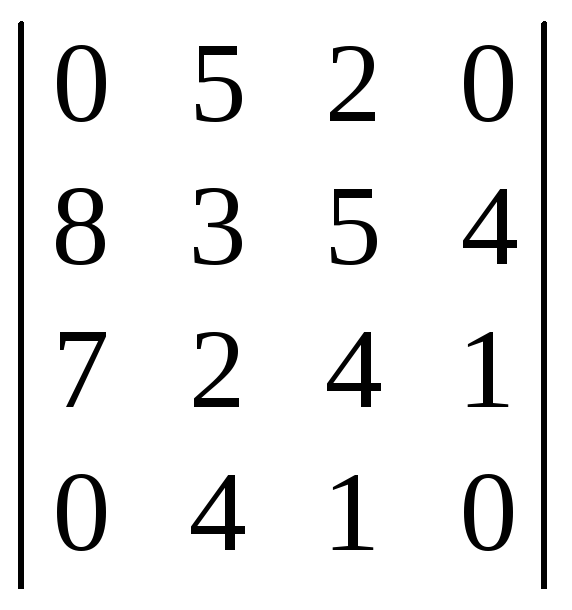 ;
; -
 ;
; -
 ;
; -
 .
.
Практическое занятие 4. Обратная матрица. Нахождение обратной матрицы с помощью линейных преобразований.
Контрольные вопросы:
-
Обратимая матрица.
План занятия.
