VI.4. Электрическое дипольное поле и излучение

Если ограничиться первым членом разложения (6.38), то векторный потенциал окажется равным

. (6.41)

Этот интеграл можно представить в более привычной форме с помощью интегрирования по частям

,

где использовано уравнение непрерывности .

Таким образом, векторный потенциал равен

, (6.42)

где величина

(6.43)

представляет собой электрический дипольный момент. Для рассмотрения гармонической составляющей потенциала, которая обладает частотой , можно также записать .

Поля электрического диполя, согласно (6.34) и (6.35), запишутся в виде

, . (6.44)

Заметим, что магнитное поле перпендикулярно радиус-вектору на любых расстояниях, а электрическое поле имеет составляющие, как параллельные, так и перпендикулярные .

В волновой зоне поля принимают асимптотическую форму

, , (6.45)

характерную для полей излучения.

Наоборот, в ближней зоне они выражаются следующим образом:

, . (6.46)

Если отвлечься от колебаний во времени, то электрическое поле совпадает с электростатическим дипольным полем. В области магнитное поле в раз меньше электрического. Поэтому, поле в ближней зоне имеет в основном электрический характер. В пределе , соответствующему статическому полю, магнитное поле исчезает, и ближняя зона распространяется до бесконечности.

В каждой точке волновой зоны поток электромагнитной энергии определяется вектором Пойтинга, усредненным по периоду колебаний

, (6.47)

где поля определяются выражениями (6.44).

Интенсивностью излучения в элемент телесного угла называется энергия, протекшая в единицу времени через элемент сферической поверхности большого радиуса r, центр которой расположен в начале координат. Вычисляя поток вектора Пойтинга (6.47) через указанный элемент сферической поверхности, находим угловое распределение интенсивности излучения

. (6.48)

Рассмотрим в качестве примера поле вертикального электрического диполя, расположенного в вакууме в начале координат и обладающего дипольным моментом . Введем декартовую систему координат и совместим ось z с осью диполя. Воспользуемся потенциалами Герца для нахождения полей.

Наряду с декартовой введем сферическую систему координат с тем же началом и полярной осью, совмещенной с осью z. Тогда, имеем следующие выражения для поля в сферической системе координат

(6.49)

В ближней зоне выражения (6.49) переходят в квазистационарное поле диполя

,

В дальней, или волновой зоне , компоненты поля приобретают следующий вид:

,

так что векторы и оказываются перпендикулярными направлению распространения волны, а отношение их амплитуд . Таким образом, в дальней зоне электрического диполя формируется локально плоская волна.

Рассмотрим диаграмму направленности дипольного излучения. Пусть имеется скалярная функция . Тогда диаграммой направленности этой функции является полярная диаграмма , где - угол, при котором функция принимает максимальное значение. Усредненный по периоду колебаний вектор плотности потока энергии (6.47) точечного электрического диполя направлен по радиусу, так что

.

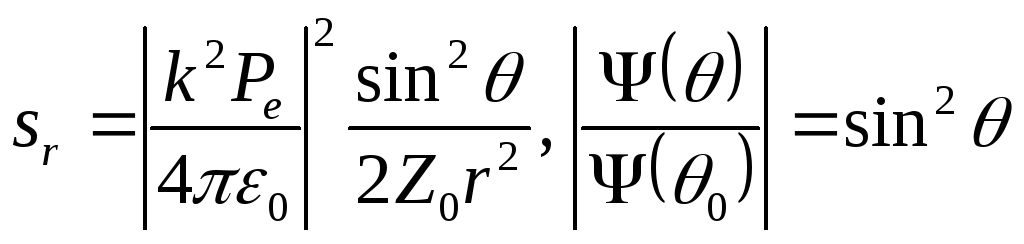Отсюда следует, что в осевом направлении диполь не излучает, максимум излучения находится при . Для углового распределения интенсивности дипольного излучения (6.48) получаем

. (6.50)

Проинтегрировав по углам, получим полную мощность излучения

. (6.51)

Для напряженности магнитного поля и интенсивности дипольного излучения во временной области имеют место также следующие формулы:

. (6.52)