
- •Сельскохозяйственная академия
- •Введение
- •1. Общие требования к оформлению домашних расчётно–графических работ.
- •По сопротивлению материалов Вариант №
- •Г. Екатеринбург 2002 г.
- •2. Растяжение (сжатие) прямого бруса - задание №1
- •2.1. Примеры решения задач.
- •2.2. Варианты домашних заданий
- •3. Геометрические характеристики плоских сечений – задание № 2.
- •Пример решения задачи
- •3.2. Варианты домашних заданий
- •Варианты домашнего задания № 2
- •4. Кручение бруса и прямой изгиб балок – задание № 3.
- •Методом начальных параметров.
- •Методом мора – верещагина
- •4.1. Примеры решения задач.
- •Решение
- •Решение
- •4.2. Варианты домашних заданий
- •Исходные данные к 1 – ой задаче задания № 3
- •5. Сложное сопротивление – задание № 4
- •5.1. Примеры решения задач
- •5.2. Варианты домашних заданий.
- •6. Расчет рамных конструкций – Задание № 5.
- •6.1 Пример расчета рамы.
- •6.2. Варианты домашних заданий
- •7. Устойчивость сжатых стержней – задание №6.
- •Примеры решения задач.
- •7.2 Варианты домашних заданий.
- •Литература:
- •Приложения
-
Методом начальных параметров.
![]()
![]()
![]()
![]()
![]() (23)
(23)
![]()
![]()
![]()
![]()
![]() (24)
(24)
Здесь
![]() и
и
![]() - прогиб и угол поворота в начале системы
координат, начало координат всегда
располагается в левом крайнем сечении
балки;
- прогиб и угол поворота в начале системы
координат, начало координат всегда
располагается в левом крайнем сечении
балки;
Z – расстояние от начала координат до сечения, где определяется прогиб и угол поворота;
а, в, с, d – расстояние от начала координат до места приложения соответствующих внешних сил m, p, q.
-
Методом мора – верещагина
Для этого строятся эпюры изгибающих
моментов от заданной внешней нагрузки
![]() (рис. 43, а), от единичной силы
(рис. 43, а), от единичной силы
![]() (рис. 43б) при определении прогиба и
единичного момента -
(рис. 43б) при определении прогиба и
единичного момента -
![]() (рис. 43в) при вычислении угла поворота,
и производится “перемножение”
соответствующих эпюр, т.е. с одной эпюры
берем ее площадь
(рис. 43в) при вычислении угла поворота,
и производится “перемножение”
соответствующих эпюр, т.е. с одной эпюры
берем ее площадь
![]() ,
а с другой – ординату
,
а с другой – ординату
![]() ,
расположенную под центром тяжести
взятой площади.
,
расположенную под центром тяжести
взятой площади.

![]()
![]()
![]()
![]()

![]() (26)
(26)
![]()
![]()
![]() (27)
(27)
Рис. 43
Основные правила перемножения эпюр:
-
результат положителен, если эпюры расположены по одну сторон от оси балки, если по разные стороны – результат отрицательный;
-
положительный результат перемножения эпюр свидетельствует о том, что направление перемещения (линейного и углового) совпадает с направлением единичных сил, при отрицательном результате – противоположны направлению единичных сил;
-
если обе эпюры (
 и
и
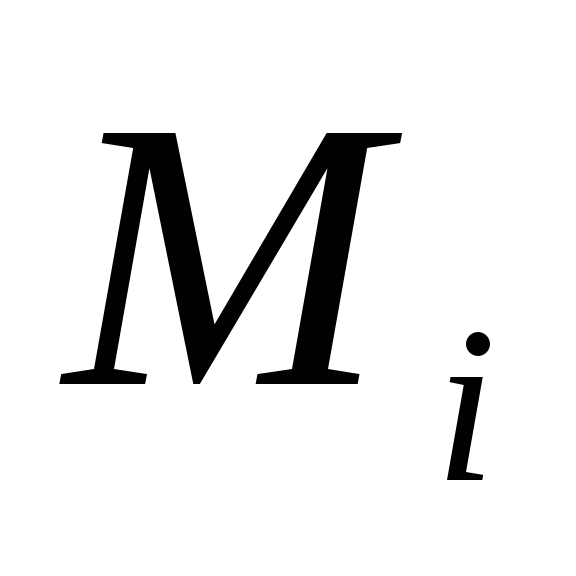 )
линейны, то не имеет принципиального
значения с какой эпюры брать площадь
)
линейны, то не имеет принципиального
значения с какой эпюры брать площадь
 ,
с какой ординату
,
с какой ординату
 ;
; -
если одна из эпюр криволинейна (это
 ),
то площадь обязательно берется с нее;
),
то площадь обязательно берется с нее; -
если сложно вычислять площадь эпюры, определить координаты центра тяжести ее и ординату
 ,
то при перемножении эпюр
,
то при перемножении эпюр
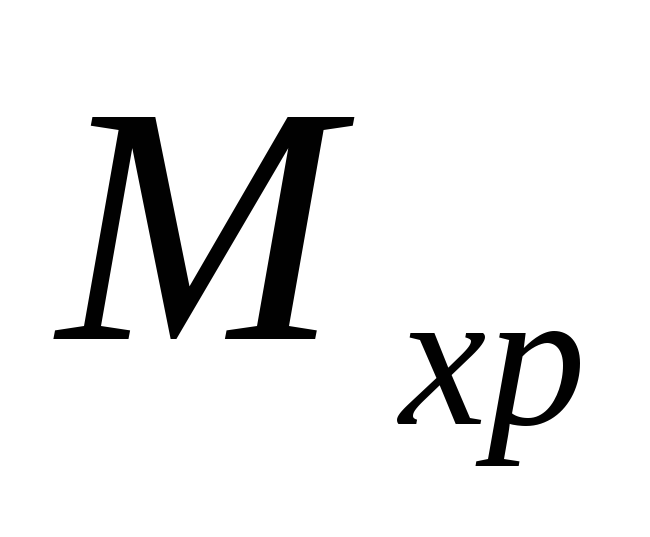 и
и
 используется прием Симсона (формула
28) (рис. 44).
используется прием Симсона (формула
28) (рис. 44).

![]() (28)
(28)
![]() А, В, С – ординаты с грузовой эпюры
А, В, С – ординаты с грузовой эпюры
![]()
а, b, с – тоже с единичной
эпюры
![]()
![]() - спина i-го участка балки
- спина i-го участка балки
Рис. 44.
4.1. Примеры решения задач.
ЗАДАЧА № 32.
Д ля
заданного вала (рис. 45) построить эпюру
крутящих моментов и определить из
условия прочности и жесткости требуемый
диаметр. Вал изготовлен из стали 45,
имеющей
ля
заданного вала (рис. 45) построить эпюру
крутящих моментов и определить из
условия прочности и жесткости требуемый
диаметр. Вал изготовлен из стали 45,
имеющей
![]() = 320 МПа, а запас по прочности К = 2,5.
Допускаемый относительный угол
закручивания
= 320 МПа, а запас по прочности К = 2,5.
Допускаемый относительный угол
закручивания
![]() .
На валу расположены 4 шкива, передающие
мощность
.
На валу расположены 4 шкива, передающие
мощность
![]() = 15 КВт,
= 15 КВт,
![]() =45 КВт,
=45 КВт,
![]() =20
КВт,
=20
КВт,
![]() =10
КВт при оборотах вала n =
955 об/мин.
=10
КВт при оборотах вала n =
955 об/мин.
Рис.45
Решение
-
Определяем величину внешних скручивающих моментов, перед каждым шкивом (через мощность и обороты вала)
![]() (кнм) (29)
(кнм) (29)
где N – мощность, КВт; n – число оборотов в минуту.
![]()
![]() кнм;
кнм;
![]() кнм;
кнм;
![]() кнм;
кнм;
![]() кнм
кнм
-
Строим эпюру крутящих моментов, разбив вал на участки I, II, III, применяя метод сечения и приняв следующее правило знаков для крутящего момента

если смотреть на оставленную часть вала со стороны сечения, то
![]() ;
;
![]()
![]()
На эпюре
![]() видно, что в сечениях, где приложены
внешние моменты получаются скачки,
равные по величине этим моментам.
Максимальная величина
видно, что в сечениях, где приложены
внешние моменты получаются скачки,
равные по величине этим моментам.
Максимальная величина
![]() = 0,30 кнм.
= 0,30 кнм.
-
Определяем диаметр вала по условиям прочности и жесткости, применяя формулы (20), предварительно определив допускаемое касательное напряжение
![]() Мпа
Мпа
![]()
![]()
здесь
![]()
![]() переведен в
переведен в
![]()
![]()
Из полученных
![]() значений принимаем диаметр вала d
= 35 мм, обеспечивая тем самым требования
и жесткости и прочности.
значений принимаем диаметр вала d
= 35 мм, обеспечивая тем самым требования
и жесткости и прочности.
ЗАДАЧА № 33. Для заданного ступенчатого
кронштейна, нагруженного внешними
окручивающими моментами m1
= 10 кНм и m2 = 30 кНм и
защемленного с обоих концов, требуется
построить эпюру крутящих моментов Мк
и при допускаемом касательном напряжении
[![]() ]
= 80 . Определить диаметры сплошной и
кольцевой частей (рис. 46). В кольцевой
части D = 2d,
d0 = 0,8d,
т. е. c =
]
= 80 . Определить диаметры сплошной и
кольцевой частей (рис. 46). В кольцевой
части D = 2d,
d0 = 0,8d,
т. е. c =
![]() =
0,4
=
0,4

Рис.46.
Решение.
1 .
Обозначив опорные моменты через m
.
Обозначив опорные моменты через m![]() и m
и m![]() ,
и составив уравнение равновесия в виде
,
и составив уравнение равновесия в виде
![]() (рис. 47а) (-mA+m1-m2+mB
= 0) мы убеждаемся, что заданная система
является статически неопределимой.
(рис. 47а) (-mA+m1-m2+mB
= 0) мы убеждаемся, что заданная система
является статически неопределимой.
Превратим ее в статически определимую,
отбросив например опору "В", заменив
ее действие опорным моментом " m![]() ".
Отбросив опору "В", мы дали возможность
сечению В поворачиваться под действием
всех внешних моментов, но ведь в заданной
системе сечение В жестко защемлено,
поворота не имеет. Отразим этот факт,
составив уравнение перемещений:
".
Отбросив опору "В", мы дали возможность
сечению В поворачиваться под действием
всех внешних моментов, но ведь в заданной
системе сечение В жестко защемлено,
поворота не имеет. Отразим этот факт,
составив уравнение перемещений:
![]() =0
(30)
=0
(30)
Рис. 47
Используя закон Гука при кручении
![]() запишем
запишем
![]()
![]()
![]()
![]()
![]()
Сократив на “a” и жесткость
“![]() ”,
получим
”,
получим
![]() (31)
(31)
Здесь
![]() и
и
![]() - полярные моменты инерции сплошной и
кольцевой частей кронштейна. Их
соотношение равно
- полярные моменты инерции сплошной и
кольцевой частей кронштейна. Их
соотношение равно
![]()
Решив уравнение (31), получим значение
опорного момента
![]()
![]()
Тогда из уравнения равновесия определяем величину опорного момента
![]()
Полученные положительные значения
опорных моментов
![]() и
и
![]() говорит о том, что их направление было
выбрано верно.
говорит о том, что их направление было
выбрано верно.
2. Разбиваем заданную систему на участки I, II, III, IV (рис. 47б). Границами участков являются сечения, где приложены внешние моменты и меняется сечение. Строим эпюры крутящих моментов (рис. 47в) применяя метод сечений
![]()
![]()
![]()
![]()
3. Из условия прочности при кручении определяем диаметры сплошной и кольцевой частей кронштейна, предварительно определив, как действуют наибольшие касательные напряжения
![]()
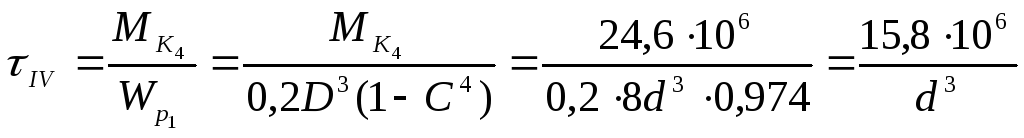
Таким образом, наибольшие касательные
напряжения действуют в значениях 2![]() участка, их и сравниваем с допускаемыми
участка, их и сравниваем с допускаемыми
![]()
Отсюда диаметр сплошной части d
равен
![]()
Тогда размеры кольцевой части кронштейна
составят
![]() ,
,
![]()
ЗАДАЧА № 34
Д ля
заданной балки построить эпюру поперечных
сил
ля
заданной балки построить эпюру поперечных
сил
![]() и изгибающих моментов
и изгибающих моментов
![]() и подобрать размеры поперечного сечения
в виде швеллера при допускаемом напряжении
и подобрать размеры поперечного сечения
в виде швеллера при допускаемом напряжении
![]() =150
Мпа.
=150
Мпа.
Рис.48
РЕШЕНИЕ
1. Введем построение эпюр
![]() и М по участкам справа, со стороны
свободного конца (рис 48а и б)
и М по участкам справа, со стороны
свободного конца (рис 48а и б)
первый участок
![]()
![]() ,
,
![]()
второй участок
![]() ,
,
![]()


третий участок
![]()
![]() ;
;
![]() ,
,
![]()
Определим координату
![]() сечения, где поперечная сила проходит
через нуль, в этом сечении изгибающий
момент
сечения, где поперечная сила проходит
через нуль, в этом сечении изгибающий
момент
![]() имеет экстремальное значение
имеет экстремальное значение
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
2. Из условия прочности на прямом изгибе
определяем размеры (номер швеллера)
сечения балки
![]() ,
,
![]()
ПО сортаменту на швеллера Гост 8240 –
82[1] и учитывая, что сечение состоит из
![]() швеллеров, принимаем швеллер № 10,
которого
швеллеров, принимаем швеллер № 10,
которого
![]() .
.
ЗАДАЧА № 35

Для
заданно шарнирно опертой балки построить
эпюры поперечных сил и изгибающих
моментов
![]() и определим с каким запасом прочности
она будет работать (рис. 49), если
и определим с каким запасом прочности
она будет работать (рис. 49), если
![]() b=60мм, h=140мм,
а=35мм.
b=60мм, h=140мм,
а=35мм.
Рис. 49
