
- •Сельскохозяйственная академия
- •Введение
- •1. Общие требования к оформлению домашних расчётно–графических работ.
- •По сопротивлению материалов Вариант №
- •Г. Екатеринбург 2002 г.
- •2. Растяжение (сжатие) прямого бруса - задание №1
- •2.1. Примеры решения задач.
- •2.2. Варианты домашних заданий
- •3. Геометрические характеристики плоских сечений – задание № 2.
- •Пример решения задачи
- •3.2. Варианты домашних заданий
- •Варианты домашнего задания № 2
- •4. Кручение бруса и прямой изгиб балок – задание № 3.
- •Методом начальных параметров.
- •Методом мора – верещагина
- •4.1. Примеры решения задач.
- •Решение
- •Решение
- •4.2. Варианты домашних заданий
- •Исходные данные к 1 – ой задаче задания № 3
- •5. Сложное сопротивление – задание № 4
- •5.1. Примеры решения задач
- •5.2. Варианты домашних заданий.
- •6. Расчет рамных конструкций – Задание № 5.
- •6.1 Пример расчета рамы.
- •6.2. Варианты домашних заданий
- •7. Устойчивость сжатых стержней – задание №6.
- •Примеры решения задач.
- •7.2 Варианты домашних заданий.
- •Литература:
- •Приложения
Г. Екатеринбург 2002 г.
2. Растяжение (сжатие) прямого бруса - задание №1
Деформация центрального растяжения (сжатая) обусловлена возникновением в любом поперечном сечении деформируемого стержня одного внутреннего усилия – ПРОДОЛЬНОЙ СИЛЫ N. Она -равна алгебраической сумме проекций внешних сил на ось стержня (ось Z) действующих на оставленную часть бруса (слева или справа от рассматриваемого сечения).
Максимальные нормальные напряжения действуют в поперечном сечении, распределены равномерно по сечению и равны:
![]()
где N – продольная сила, Н;
F – площадь поперечного сечения, мм2
Единица измерения напряжения – МЕГАПАСКАЛЬ – МПа, IМПа=IН/мм2
Прочность деформируемого элемента конструкций обеспечивается, если
![]()
где
![]() -
допускаемое напряжение для материала
стержня.
-
допускаемое напряжение для материала
стержня.
Оно равно
![]() (пластичные
материалы)
(пластичные
материалы)
Или
![]() (хрупкие
материалы)
(хрупкие
материалы)
![]()
Здесь
![]() и
и
![]() - соответственно предел текучести и
предел прочности материала;
- соответственно предел текучести и
предел прочности материала;
К – требуемый коэффициент запаса прочности.
Относительная (![]() )
или абсолютная (
)
или абсолютная (![]() )
продольная деформация определяется по
закону Гука
)
продольная деформация определяется по
закону Гука
![]() и
и
![]()
где Е – модуль продольной упругости, величина постоянная для каждого материала, для сталей Е=2*105 МПа.
l- длина стержня, мм.
Поперечная относительная деформация равна
![]()
где
![]() -
коэффициент поперечной деформации
(коэф. Пуассона), для сталей
-
коэффициент поперечной деформации
(коэф. Пуассона), для сталей
![]() .
.
2.1. Примеры решения задач.
Задача №1
Д ля
заданного ступенчатого стержня (рис.1.)
построить эпюры продольных сил и
нормальных напряжений, определить
перемещения сечения АА, если Р1=50
кН; Р2=150 кН; Р3=30 кН; а=0,4 м;
F=2,5 см2.
ля
заданного ступенчатого стержня (рис.1.)
построить эпюры продольных сил и
нормальных напряжений, определить
перемещения сечения АА, если Р1=50
кН; Р2=150 кН; Р3=30 кН; а=0,4 м;
F=2,5 см2.
Рис. 1.
Решение
-
Разбиваем стержень на участки 1,2,3,4, границами которых являются сечения, где приложены внешние силы и меняются размеры сечения.
-
Применяя метод сечения, определяем продольные силы по участкам. Построение эпюры ведём справа, со свободного конца. Проведя произвольное сечение на 1 участке и рассматривая условие равновесия правой оставленной части, можем записать (см.рис.2а)

![]()
Поступая аналогично для второго участка, будем иметь (см.рис.2б)
![]()
Рис.2
Продольные силы и нормальные напряжения, направленные от сечения и вызывающие деформацию растяжения будем считать положительными, направленными к сечению и вызывающим деформацию сжатия – отрицательными.
Эпюра продольных сил N представлена на рис. 1а. В сечениях, где приложены внешние силы, получили скачки, равные этим словам.
-
Зная величину продольной силы на каждом участке и используя формулу (1), определяем нормальные напряжения, действующие в поперечных сечениях (рис. 1б):

-
Перемещение сечения А-А определяется деформацией части стержня, расположенного между неподвижным сечением (заделкой) и рассматриваемым сечением А-А.

Сечение А-А переместиться влево на 1,65 мм.
Задача №2
О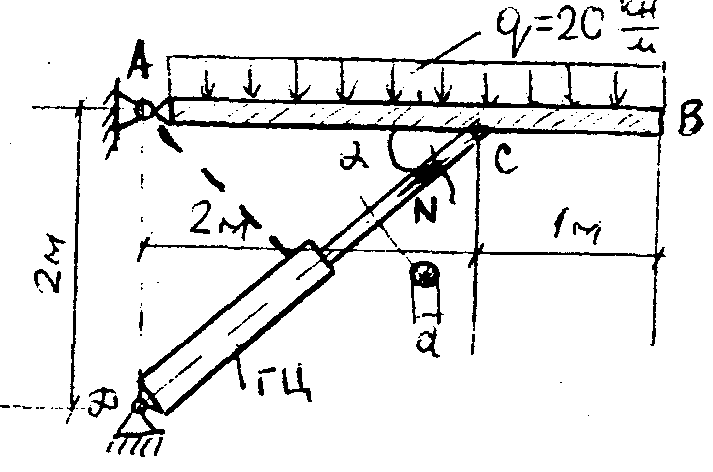 пределить
диаметр d штока гидроцилиндра ГЦ,
поддерживающего жесткую плиту АВ стенда
для мойки тракторов (рис.3.) если он
изготовлен из стали 45, имеющей
пределить
диаметр d штока гидроцилиндра ГЦ,
поддерживающего жесткую плиту АВ стенда
для мойки тракторов (рис.3.) если он
изготовлен из стали 45, имеющей
![]() ,
а необходимый запас по прочности К=3.
,
а необходимый запас по прочности К=3.
Рис.3.
Решение.
-
Делаем сечение, обозначаем усилие в штоке при N. Из условия равновесия системы определяем усилие в штоке. Он испытывает деформацию сжатия.
-

-
Применив условие прочности (2) при растяжении (сжатии) определяем диаметр штока
![]()
Округляем до ГОСТовских значений d=30мм.
Задача №3

Для заданного стального ступенчатого стержня, защемлённого с обеих сторон (рис 4.), построить эпюр продольных сил и определить максимальное нормальное напряжение в опасном сечении, если
Р=300кН; а=0,25 м; F=2 см2, Е=2*105 МПа.
Определить также величину полной потенциальной энергии деформации.
Рис.4.
Решение
-
Обозначим опорные реакции Ra и Rb и составив уравнение равновесия системы в виде

-Ra+P-Rb=0 Ra+Rb=P (1)
видим, что реакции определить не можем. Не зная реакции, мы не сможем определить с помощью метода сечений внутренние усилия- продольные силы. Следовательно, заданная система является статически неопределимой. Для её расчёта необходимо составить дополнительное уравнение перемещений. Превращаем заданную систему в статически определимую, отбросив одну из опор, например опору В (см. рис 4а). действие опоры В заменяем реакцией Rв. Отбросив опору В, мы дали возможность сечению В под действием сил Р и Rв перемещаться, но в заданной системе сечение В не имеет перемещений (жёсткая заделка).
Отразив этот факт, мы получаем необходимое уравнение перемещения
![]()
Используя закон Гука, можем записать (см. рис. 4б.в.)
![]()
Поставив значения перемещения (3) в уравнение (2), и решив его, получим
![]()
Тогда из (1) RA=P-RB =300-100=200кН.
-
Строим эпюры продольных сил по участкам (см. рис. 5)

Н ормальные
напряжения в поперечных сечениях равны
ормальные
напряжения в поперечных сечениях равны
Рис.5.

-
Полная потенциальная энергия деформации стержня равна сумме энергий, накапливаемых на каждом участке

Задача №4
Ж есткая
плита АВ поддерживается двумя стальными
стержнями одинакового сечения (рис.6.)
есткая
плита АВ поддерживается двумя стальными
стержнями одинакового сечения (рис.6.)
Определить, какие возникнут температурные напряжения в обоих стержнях, если будет нагреваться только 1 стержень на 800 . Коэф. температурного расширения стали а=12*10-6 , Е=2*105 МПа.
Рис.6.
Решение.
-
Вследствие нагрева 1 стержень, стремясь расширится (удлиниться) будет воздействовать на второй стержень, вызывая в нём сжимающее усилие N2. Второй стержень, сопротивляясь, будет тоже воздействовать на 1 стержень, вызывая в нём сжимающее усилие N1. Для определения этих усилий составим уравнение равновесия системы в виде
![]()
Таким образом, имеем одно уравнение с
2-мя неизвестными усилиями. Следовательно,
система является статически неопределимой.
Для её расчёта составляем уравнение
перемещений из следующих рассуждений
(см. рис. 7): если бы в конструкции не было
второго стержня, то 1 стержень за счёт
нагрева получил бы температурное
удлинение
![]()
![]() В
действительности же второй стержень,
сопротивляясь, будет ограничивать
температурное удлинение 1 стержня. Точка
приложения усилия N1 получит
перемещение
В
действительности же второй стержень,
сопротивляясь, будет ограничивать
температурное удлинение 1 стержня. Точка
приложения усилия N1 получит
перемещение
![]() ,
которое очевидно будет равно
,
которое очевидно будет равно
![]()
Точка приложения усилия N2 получает
перемещение
![]() ,
которое, спроектировав на направление
действия усилия N2 , можем выразить
через его деформацию
,
которое, спроектировав на направление
действия усилия N2 , можем выразить
через его деформацию
![]()
![]()
Используя подобие прямоугольных
треугольников с катетами
![]() ,
,![]() ,
5 и 3 м, запишем
,
5 и 3 м, запишем
![]()
с учётом выражений (2) и (3) будем иметь
![]()
Из рис.6. видно, что
![]()
Решая совместно уравнение (1) и (4), определяем усилия в стержнях

-
Температурные нормальные напряжения, возникающие в стержнях будут равны

Задача №5
Ж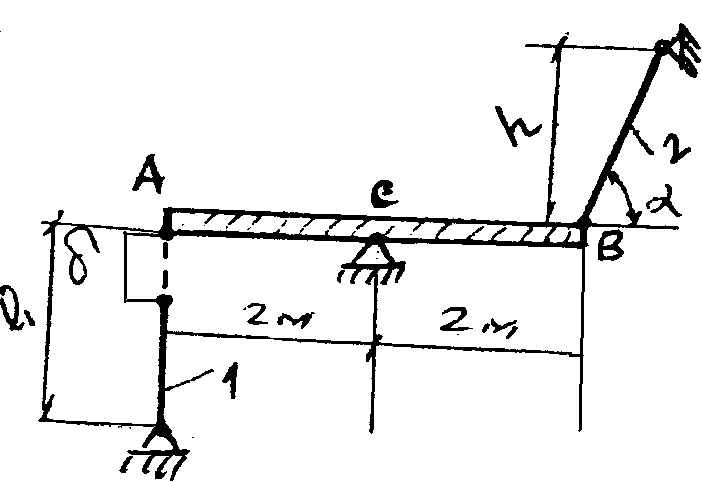 ёсткая
плита АВ должна поддерживаться двумя
стальными стержнями 1 и 2, у которых
сечения равны F1=F; F2=0,8F
(рис.8). При изготовлении 1 стержень
оказался короче требуемой длины на
величину
ёсткая
плита АВ должна поддерживаться двумя
стальными стержнями 1 и 2, у которых
сечения равны F1=F; F2=0,8F
(рис.8). При изготовлении 1 стержень
оказался короче требуемой длины на
величину
![]() .
Определить, какие монтажные напряжения
возникнут в стержнях при сборке
конструкции, если
.
Определить, какие монтажные напряжения
возникнут в стержнях при сборке
конструкции, если
Рис.8.
![]()
Решение
-
При сборке конструкции (рис. 8.) зазор
 мы будем «закрывать» очевидно за счёт
деформации растяжения 1 стержня -
мы будем «закрывать» очевидно за счёт
деформации растяжения 1 стержня -
 и перемещения
и перемещения
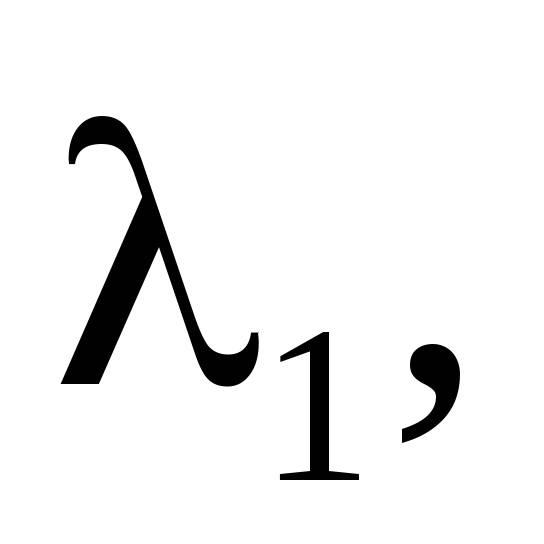 обусловленного деформацией сжатия
стержня 2 (рис. 9). Составим уравнение
равновесия системы в виде
обусловленного деформацией сжатия
стержня 2 (рис. 9). Составим уравнение
равновесия системы в виде

![]() =0,
т.е. N1 = 0.866 N2
(1)
=0,
т.е. N1 = 0.866 N2
(1)

Рис.9
Отсюда следует, что система статически неопределима. Дополнительное уравнение перемещений составим, рассматривая характер деформации конструкции (см.рис.9).
Очевидно, что
![]() ,
но из подобия треугольников видим, что
,
но из подобия треугольников видим, что
![]()
Перемещение
![]() точки приложения усилия N2 выразим
через деформацию укорочения стержня
2.
точки приложения усилия N2 выразим
через деформацию укорочения стержня
2.
![]()
Таким образом, получим после преобразований

N2=![]()
С учётом выражения (1), усилие в 1 стержне составит
N1=0,866*0,204*10-3![]() =
0,176*10-3
=
0,176*10-3![]()
-
Монтажные напряжения в стержнях очевидно будут равны

