- •Предмет курса, его цели и задачи.
- •Рыночная экономика и степени рисков предпринимательства.
- •Математическое моделирование предпринимательской деятельности.
- •1. Предмет курса, его цели и задачи.
- •2. Рыночная экономика и степени рисков предпринимательства.
- •3. Математическое моделирование предпринимательской деятельности.
- •2. Методы исследования и оценки эффективности бизнес-процессов.
- •3. Основные задачи маркетинга и менеджмента хозяйственной деятельности предприятий.
- •4. Структура алгоритма математического моделирования бизнес-процессов.
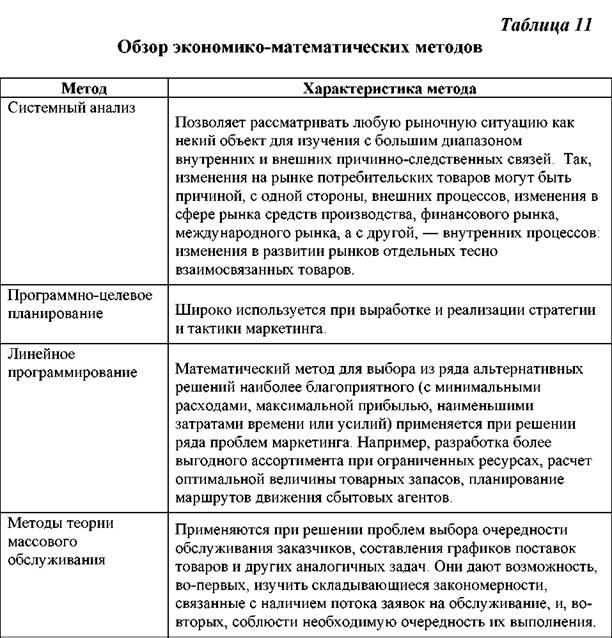
- •2.Систематизация математических методов при экономико-математическом моделировании бизнес-процессов.
- •3.Математические модели и методы решения типовых задач оценки эффективности бизнес-процессов.
- •4.Методы оптимизации бизнес-процессов.
- •Методы анализа и прогноза маркетинга.
- •Метод экспертных оценок и его развитие – метод доминирующих оценок. Использование метода доминирующих оценок в задачах маркетинга и менеджмента разных видов деятельности.
- •Диверсификация производства и продукции, государственный и коммерческий заказ, внешнеэкономическая деятельность.
- •Постановка задачи оптимизации структуры хозяйственной деятельности предприятия.
2. Методы исследования и оценки эффективности бизнес-процессов.
|
|
3. Основные задачи маркетинга и менеджмента хозяйственной деятельности предприятий.
Сфера управления маркетингом, занимая определенное место в общей системе маркетинговых знаний, включает анализ, планирование, контроль за проведением мероприятий, рассчитанных на установление, укрепление и поддержание выгодных обменов посредством решения определенных задач организации, таких как получение прибыли, рост объема сбыта, увеличение доли рынка и т.д. В сфере менеджмента, непосредственно соприкасающейся с управлением маркетингом на фирме и маркетинговым управлением фирмой, выступают мотивация фирмы, оценка хозяйственных решений, стратегическое планирование, выбор формы хозяйствования, структура управления, управление персоналом, имитационное моделирование и др.
Такие функции управления, как целеполагание, прогнозирование, планирование, представляют собой, по сути, обоснование и принятие управленческих решений, реализуемых в рамках информационно—аналитических задач маркетинга.
Менеджмент может быть ориентирован на человека и на проблему. В первом случае важнейшей стороной менеджмента как вида профессиональной деятельности субъектов (менеджеров) является умение управлять персоналом. Во втором случае речь идет о деловой интуиции, которая определяется умением менеджеров осуществлять (самостоятельно или при поддержке специалистов) постановку и решение задач управления.
Задача управления сводится к тому, чтобы согласовывать субъективную деятельность людей по управлению с требованиями рынка и определяемыми им прогрессивными тенденциями, что позволяет правильно оценить реальную обстановку и направление ее развития, условия функционирования рыночных отношений.
|
4. Структура алгоритма математического моделирования бизнес-процессов.
Математические модели, используемые для описания экономических процессов и явлений называют экономико-математическими моделями. Для классификации этих моделей используются разные основания.
По целевому назначению экономико-математические модели делятся на теоретико-аналитические, используемые в исследованиях общих свойств и закономерностей экономических процессов , и прикладные, применяемые в решении конкретных экономических задач (модели экономического анализа, прогнозирования, управления).
При классификации моделей по исследуемым экономическим процессам и содержательной проблематике можно выделить модели экономики в целом и ее подсистем - отраслей, регионов и т.д., комплексы моделей производства, потребления и т. д.
С точки зрения общей классификацией математических моделей они подразделяются на функциональные и структурные, а также включают промежуточные формы (структурно-функциональные). Типичными структурными моделями являются модели межотраслевых связей.
Существует классификация моделей на дескриптивные и нормативные. Дескриптивные модели отвечают на вопрос: как это происходит? или как это вероятнее всего может дальше развиваться? То есть они только объясняют наблюдаемые факты или дают вероятный прогноз. Примерами дескриптивных моделей являются производственные функции и функции покупательского спроса, построенные на основе обработки статистических данных.
Нормативные модели отвечают на вопрос: как это должно быть? То есть предполагают целенаправленную деятельность. Примером нормативных моделей являются модели оптимального планирования, формализующие тем или иным способом цели экономического развития, возможности и средства их достижения.
Многие экономико-математические модели сочетают признаки дескриптивных и нормативных моделей. Например, межотраслевая модель может включать функции покупательского спроса, описывающие поведение потребителей при изменении доходов.
По характеру отражения причинно-следственных связей различают модели жестко детерминистские и модели, учитывающие случайность и неопределенность.
По способам отражения фактора времени экономико-математические модели делятся на статические и динамические. В статических моделях все зависимости относятся к одному моменту или периоду времени. Динамические модели характеризуют изменения экономических процессов во времени.
Модели экономических процессов разнообразны по форме математических зависимостей. Особенно важно выделить класс линейных моделей, наиболее удобных для анализа и вычислений и получивших вследствие этого большое распространение.
По соотношению экзогенных (требования рынка) и эндогенных (ресурсы) переменных, включаемых в модель, модели могут разделяться на открытые и закрытые. Полностью открытых моделей не существует; модель должна содержать хотя бы одну эндогенную переменную. Полностью закрытые экономико-математические модели, т.е. не включающие экзогенных переменных, исключительно редки.
Существует также деление моделей на агрегированные и детализированные.
В зависимости от того, включают ли модели пространственные факторы и условия или не включают, различают модели пространственные и точечные.
Основные этапы процесса моделирования ЭММ:
1 этап. Постановка экономической проблемы и ее качественный анализ. Этот этап включает выделение важнейших черт и свойств моделируемого объекта и абстрагирование от второстепенных; изучение структуры объекта и основных зависимостей, связывающих его элементы; формулирование гипотез (хотя бы предварительных), объясняющих поведение и развитие объекта.
2 этап. Построение математической модели. Это - этап формализации экономической проблемы, выражения ее в виде конкретных математических зависимостей и отношений (функций, уравнений, неравенств и т.д.).
3 этап. Математический анализ модели. Целью этого этапа является выяснение общих свойств модели. Здесь применяются чисто математические приемы исследования. Модели сложных экономических объектов с большим трудом поддаются аналитическому исследованию. В тех случаях, когда аналитическими методами не удается выяснить общих свойств модели, а упрощения модели приводят к недопустимым результатам, переходят к численным методам исследования.
4 этап. Подготовка исходной информации. Моделирование предъявляет жесткие требования к системе информации. В то же время реальные возможности получения информации ограничивают выбор моделей, предназначаемых для практического использования.
5 этап. Численное решение. Этот этап включает разработку алгоритмов для численного решения задачи, составления компьютерных программ и непосредственное проведение расчетов.
6 этап. Анализ численных результатов и их применение. На этом заключительном этапе цикла встает вопрос о правильности и полноте результатов моделирования, о степени практической применимости последних.
Лекция 3. Математические методы моделирования бизнес-процессов.
-
Классификационные признаки математических методов при решении прикладных задач.
-
Систематизация математических методов при экономико-математическом моделировании бизнес-процессов.
-
Математические модели и методы решения типовых задач оценки эффективности бизнес-процессов.
-
Методы оптимизации бизнес-процессов.
1.Классификационные признаки математических методов при решении прикладных задач.
По функциональному признаку и целям содержательные модели делятся на описательные, объяснительные и прогностические. Описательной моделью называется любое описание объекта. Объяснительная модель позволяет ответить на вопрос: почему это происходит? Прогностическая модель описывает будущее поведение объекта.
Концептуальная (содержательная) модель - это абстрактная модель, определяющая структуру моделируемой системы, свойства ее элементов и причинно-следственные связи, присущие системе и существенные для достижения цели моделирования. Иными словами, это содержательная модель, при формулировании которой используются понятия и представления предметных областей, связанных с моделью. Например, ММ формулируется на языке математики – с помощью математических структур: формул, пространственных форм и т.п.
Выделяют три вида концептуальных моделей: логико-семантические, структурно-функциональные и причинно-следственные.
Логико-семантическая модель – описание объекта в терминах соответствующих предметных областей знаний. Анализ таких моделей осуществляется средствами логики с привлечением специальных знаний.
При построении структурно-функциональной модели объект рассматривается как целостная система, которую расчленяют на отдельные подсистемы или элементы. Части системы связывают структурными отношениями, описывающими подчиненность, логическую и временную последовательность решения задач.
Причинно-следственная модель служит для объяснения и прогнозирования поведения объекта. Такие модели ориентированы на следующие моменты: 1) выявление главных взаимосвязей между подсистемами; 2) выявление определенного влияния различных факторов на состояние объекта; 3) описание динамики интересующих разработчика параметров.
Формальная модель является представлением концептуальной модели с помощью формальных языков. К таким языкам относятся математический аппарат, алгоритмические языки, языки моделирования.
Построение концептуальной модели включает следующие этапы:
1) определение типа системы;
2) описание внешних воздействий;
3) декомпозиция системы.
На первом этапе осуществляется сбор фактических данных (на основе работы с литературой и технической документацией, проведения натурных экспериментов, сбора экспертной информации и т. д.), а также выдвижение гипотез относительно значений параметров и переменных, для которых отсутствует возможность получения фактических данных.
Одним из классификационных признаков моделируемой системы является мощность множества состояний моделируемой системы. По этому признаку системы делят на статические и динамические. Система называется статической, если множество ее состояний содержит один элемент. Если состояний больше одного, или они могут изменяться во времени, система называется динамической. Процесс смены состояний называется движением системы.
Различают два основных типа динамических систем:
– с дискретными состояниями (множество состояний конечно или счетно);
– с непрерывным множеством состояний.
Системы с дискретными состояниями характеризуются тем, что в любой момент времени можно однозначно определить, в каком именно состоянии находится система. Для такой идентификации обязательно нужно знать тот признак, который отличает одно состояние системы от другого. Например, при исследовании систем массового обслуживания в качестве такого признака обычно используют число заявок в системе.
По условиям перехода из одного состояния в другое различают детерминированные системы и стохастические.
В детерминированных системах новое состояние зависит только от времени и текущего состояния системы. Другими словами, если имеются условия, определяющие переход системы в новое состояние, то для детерминированной системы можно однозначно указать, в какое именно состояние она перейдет.
Для стохастической системы можно указать лишь множество возможных состояний перехода и, в некоторых случаях, - вероятностные характеристики перехода в каждое из этих состояний.
Рассмотренная схема классификации систем важна не сама по себе. На этапе разработки концептуальной модели она, во-первых, позволяет уточнить цели и задачи моделирования и, во-вторых, облегчает переход к этапу формализации модели. Кроме того, значительно позже, на этапе оценки качества разработанной модели, знание классификационных признаков дает возможность оценить степень ее соответствия первоначальному замыслу разработчика.
Рассмотренные классификационные признаки применимы и для определения типа разрабатываемой модели. При этом исследуемая система и ее модель могут относиться как к одному, так и к разным классам. Например, реальная система может быть подвержена воздействию случайных факторов и, соответственно, будет относиться к классу стохастических систем. Если разработчик модели считает, что влиянием этих факторов можно пренебречь, то создаваемая модель будет представлять собой детерминированную систему. Аналогичным образом возможно отображение системы с непрерывным временем смены состояний в модель с дискретными переходами и т. д.
Совокупность факторов, воздействующих на систему и оказывающих влияние на эффективность её функционирования, назовем внешними воздействиями (ВВ).
Модель внешних воздействий должна обладать следующими основными свойствами:
– совместимостью с моделью системы;
– представительностью;
– управляемостью;
– системной независимостью.
Свойство совместимости предполагает, что, во-первых, степень детализации описания ВВ соответствует детализации описания системы; во-вторых, модель ВВ должна быть сформулирована в тех же категориях предметной области, что и модель системы (например, если в модели системы исследуется использование ресурсов, то должны быть выражена в запросах на ресурсы).
Представительность модели ВВ определяется ее способностью адекватно представить ВВ в соответствии с целями исследования. Другими словами, модель ВВ должны отвечать целям исследования системы. Например, если оценивается пропускная способность, то должны выбираться ВВ, «насыщающие» систему. Под управляемостью понимается возможность изменения параметров модели ВВ в некотором диапазоне, определяемом целями исследования.
Системная независимость - это возможность переноса модели ВВ с одной системы на другую с сохранением ее представительности. Данное свойство наиболее важно при решении задач сравнения различных систем или различных модификаций одной системы. Если модель ВВ зависит от конфигурации исследуемой системы или других ее параметров, то использование такой модели для решения задачи выбора невозможно,
И, наконец, обратимся к этапу, завершающему построение концептуальной модели системы, - ее декомпозиции.
Декомпозиция системы производится исходя из выбранного уровня детализации модели, который, в свою очередь, определяется тремя факторами:
– целями моделирования;
– объемом априорной информации о системе;
– требованиями к точности и достоверности результатов моделирования.
Уровни детализации иногда называют стратами, а процесс выделения уровней - стратификацией. Детализация системы должна производиться до такого уровня, чтобы для каждого элемента были известны или могли быть получены зависимости его выходных характеристик от входных воздействий, существенные с точки зрения выбранного показателя эффективности. Повышение уровня детализации описания системы позволяет получить более точную ее модель, но усложняет процесс моделирования и ведет к росту затрат времени на его проведение. Например, если моделируется дискретная система, то увеличение детальности ее описания означает увеличение числа различных состояний системы, учитываемых в модели, и, как следствие - неизбежный рост объема вычислений.