
БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
ФАКУЛЬТЕТ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ
КАФЕДРА УПРАВЛЕНИЯ И ИНФОРМАТИКИ В ТЕХНИЧЕСКИХ СИСТЕМАХ
ЛАБОРАТОРНАЯ РАБОТА №2
по дисциплине
Теория автоматического управления
Исследование устойчивости и качества линейных импульсных систем
Выполнил ст. гр. УИТ-41
Печавин А. В.
Проверил преподаватель
Мартынова И. В._______
«___» ___________2005
2005
Цель работы: исследовать влияние параметров ЛИС на устойчивость и качество переходных процессов.
Данные: передаточная
функция системы![]() ,
параметры T=0.25;
K=1.5;
T1=2;
d1=0.8.
Передаточная функция примет вид:
,
параметры T=0.25;
K=1.5;
T1=2;
d1=0.8.
Передаточная функция примет вид:
![]()
-
Найдем дискретную передаточную функцию разомкнутой системы используя матричный метод.
По заданной передаточной функции запишем дифференциальное уравнение:
4y’’ + 3.2y’ + y =1.5u
Перейдем к уравнениям в пространстве состояний:
y = x1
y’ = x’1 = x2 4x’2 + 3.2x2 + x1 = 1.5u
y’’ = x’2
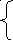 x’1
= x2
x’1
= x2
x’2 = -0.25x1 – 0,8х2 + 0.375u
y = x1
![]()
=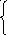 >
X’ =
>
X’ =
Y = (1 0)x
Следовательно, матрицы:
![]()
![]()
![]()
![]()
![]()
= ; = ; = (1 0)
По формуле (4) определим матрицы А и В
![]()
![]()
![]()
![]()
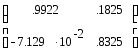
![]() +
0,2 + 2·
=
+
0,2 + 2·
=
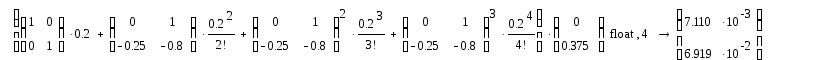
Матрицы С и совпадают.
Разностные уравнения имеют вид:

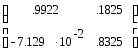
 X’(k+1)
=
x(k) + u(k)
X’(k+1)
=
x(k) + u(k)
Y(k) = (1 0)x(k)
Дискретную передаточную функцию с фиксатором нулевого порядка находим по формуле:
W(z) = C{ZI-A}-1B

![]()
![]()
{zI – A}-1 = =
W(z) = (1
0)
![]() =
=
![]()
-
Определим дискретную передаточную функцию замкнутой системы
![]()
После подстановки и упрощения получим:
![]()
-
Определим устойчивость системы по критерию Шур-Кона
Характеристическое уравнение замкнутой системы имеет вид:
![]()
Для уравнения второго порядка воспользуемся следующими условиями:
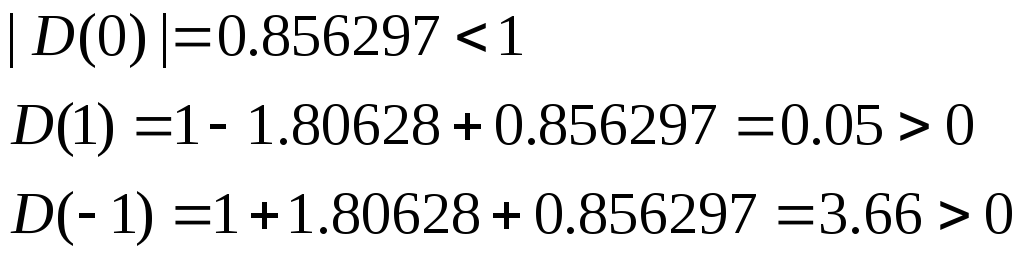
Согласно критерию, система устойчива.
-
Исследуем систему с помощью билинейного преобразования
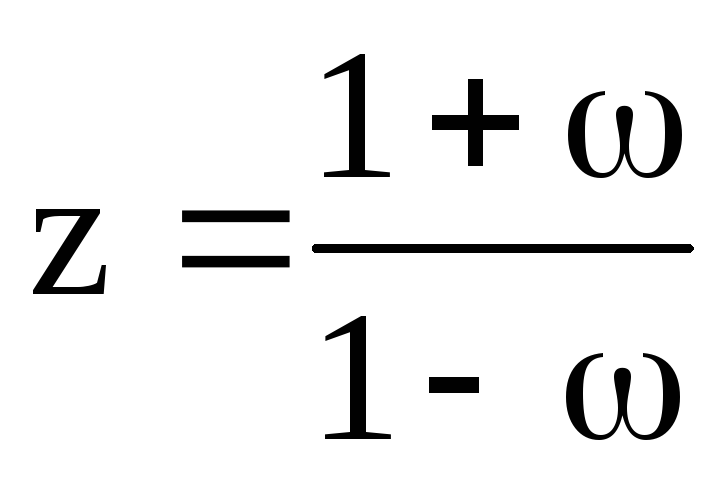 .
.
Характеристическое уравнение замкнутой системы представим в ω-форме:
![]()
Получим:
![]()
или
![]()
Для анализа устойчивости этого уравнения используем критерий Гурвица.
а0=1,94998>0
Δ1=а1=2>0
Согласно критерию, система устойчива.
-
Модели непрерывной системы в замкнутом состоянии представлены на рисунке 1. Причем вторая модель с установленным в системе интегратором, а третья с найденным значением K, при котором система находится на границе устойчивости. На рисунке 2 представлены переходные характеристики построенных моделей.
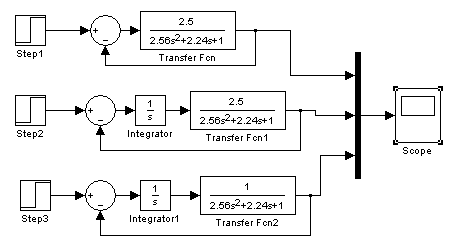
Рисунок 1 – Модели непрерывной системы
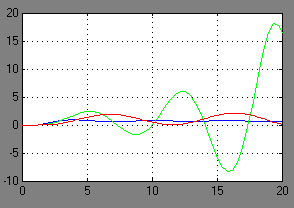
Рисунок 2 – Переходные процессы непрерывной системы
Модели импульсных систем:
-
непрерывная система с экстраполятором нулевого порядка;
-
непрерывная система с дискретной передаточной функцией, включающей передаточную функцию экстраполятора;
-
непрерывная система с экстраполятором нулевого порядка;
-
непрерывная система с экстраполятором нулевого порядка с коэффициентом К, выводящем систему на границу устойчивости;
-
непрерывная система с экстраполятором и цифровым интегратором с коэффициентом К, выводящем систему на границу устойчивости.
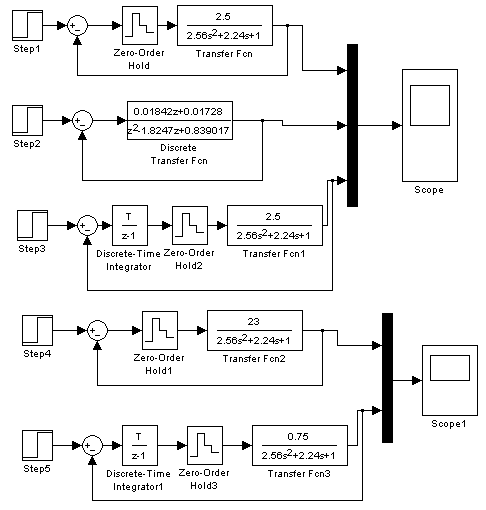
Рисунок 3 – Модели ЛИС
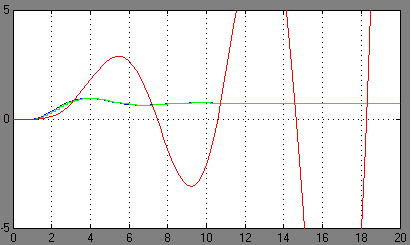
Рисунок 4 – Переходные характеристики систем 1, 2 и 3
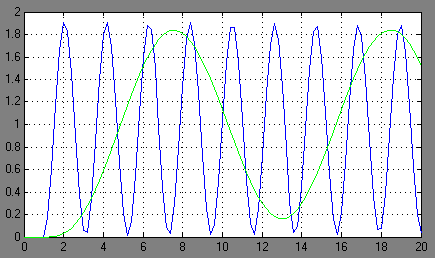
Рисунок 5 – Переходные характеристики систем 4 и 5
