Министерство образования РФ
Балаковский институт техники, технологии и управления
Лабораторная работа № 1
Вариант № 15
Построение и исследование математических моделей
линейных импульсных систем (ЛИС)
Выполнил ст. гр. УИТ-41
Печавин А.В.
Проверил: Мартынова И. В.
Балаково, 2005
Передаточная функция непрерывной части системы имеет вид:
![]()
W0(p) = . Шаг дискретизации Т = 0,2.
1. Определить передаточную функцию дискретной системы W(z), используя матричный метод.
По заданной передаточной функции запишем дифференциальное уравнение:
2.56y” + 1.76y’ + y = 3u
Перейдем к уравнениям в пространстве состояний
y = x1
y’ = x’1 = x2 2.56x’2 + 1.76x2 + x1 = 3u
y” = x’2
 x’1 = x2
x’1 = x2
x’2 = -0.390625x1 – 0,6875х2 + 1,171875u
y = x1
![]()
=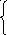 >
X’ =
>
X’ =
Y = (1 0)x
Следовательно, матрицы:
![]()
![]()
![]()
![]()
![]() = ; = ; = (1 0)
= ; = ; = (1 0)
По формуле (4) определим матрицы А и В
![]()
![]()
![]()
![]()
![]()
![]() + 0,2 + 2·
=
+ 0,2 + 2·
=

![]()
Матрицы С и совпадают.
Разностные уравнения имеют вид:
![]()
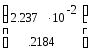
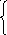 X’(k+1) = x(k) +
u(k)
X’(k+1) = x(k) +
u(k)
Y(k) = (1 0)x(k)
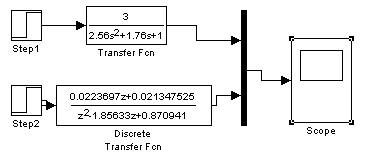
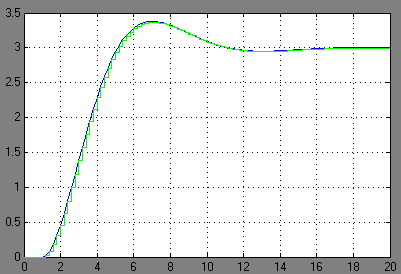
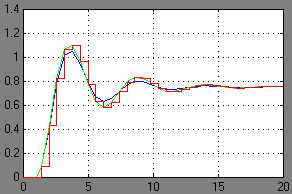
По найденному разностному уравнению составлена математическая модель системы, реализованная в Simulink. Структурная схема представлена на рисунке.
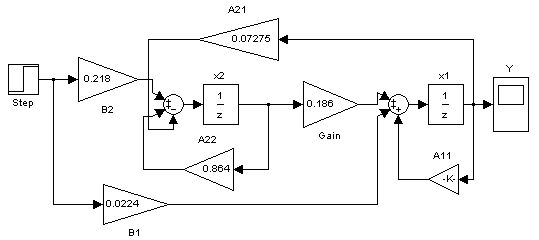
Рисунок – структурная схема дискретной системы
Дискретную передаточную функцию с фиксатором нулевого порядка находим по формуле:
W(z) = C{ZI-A}-1B
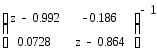
![]()
![]()
{zI – A}-1 = =
W(z) = (1 0) =
2. Найдем дискретную передаточную функцию с использованием z-преобразований
![]() , Т = 0,2
, Т = 0,2
Разобьем исходную передаточную функцию на элементарные дроби.