
БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
ФАКУЛЬТЕТ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ
КАФЕДРА УПРАВЛЕНИЕ И ИНФОРМАТИКА В ТЕХНИЧЕСКИХ СИСТЕМАХ
ЛАБОРАТОРНАЯ РАБОТА №2
по дисциплине ТАУ
ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ И КАЧЕСВО ЛИНЕЙНЫХ
ИМПУЛЬСНЫХ СИСТЕМ (ЛИС)
Выполнил ст. гр. УИТ-..
…
Принял преподаватель
…
2011
Цель работы: исследовать влияние параметров ЛИС на устойчивость и качество переходных процессов.
Вариант 25
Передаточная
функция непрерывной части системы имеет
вид:
![]() .
Шаг дискретизации T=0,3.
.
Шаг дискретизации T=0,3.
Упростив
![]() ,
получим:
,
получим:
![]()
1 Найдем дискретную передаточную функцию разомкнутой системы с использованием z – преобразований.
![]()
![]() .
.
Разобьём исходную передаточную функцию на элементарные дроби:
![]()
![]() =
=![]()
![]()
![]() =
=![]()
![]()
![]() .
.
Для
каждой дроби запишем соответствующие
z-преобразования,
и их сумму умножим на
![]() .
.
![]()
После упрощения получим следующий вид дискретной передаточной функции с фиксатором нулевого порядка.
Wр(z)=
![]()
2 Определим дискретную передаточную функцию замкнутой системы.
![]()
После подстановки и упрощения имеем:
W(z)=
![]()
3 Определим устойчивость системы по критерию Шур – Коне.
Характеристическое уравнение замкнутой системы имеет вид:
![]()
Для характеристического уравнения 2 порядка условие Шур – Кона выражается следующим образом:
![]()
![]()
![]()
Тогда, для нашего случая имеем:
![]()
![]()
![]()
4
Исследуем систему с помощью билинейного
преобразования
![]() .
.
Характеристическое
уравнение замкнутой системы представим
в
![]() - форме.
- форме.
![]()
Получим
![]()
или
![]() .
.
Для анализа устойчивости этого уравнения используем критерий Гурвица.
![]()
![]()
Следовательно, система устойчива.
5 Модели непрерывной системы в замкнутом состоянии представлены на рисунке 1. Причем, вторая модель с установленным в системе интегратором, а третья с подобранным значением К, при котором система находиться на грани устойчивости. На рисунке 2 представлены переходные характеристики построенных моделей.
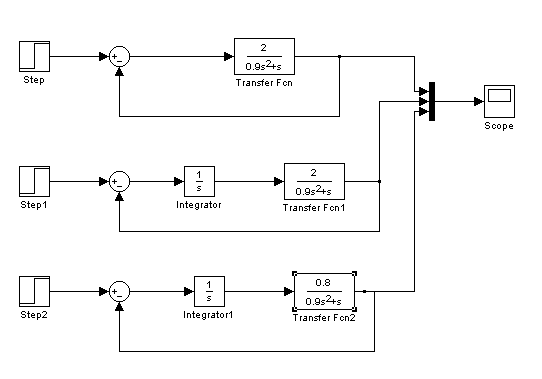
Рисунок 1 – Модели непрерывной системы
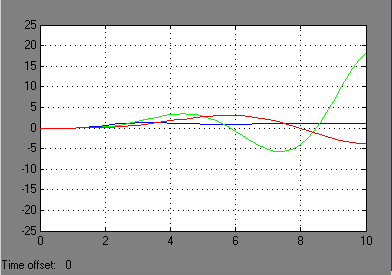
Рисунок 2 – Переходные процессы непрерывной системы
На рисунке 3 изображены модели импульсных систем:
1 – Непрерывная система с экстраполятором нулевого порядка;
2 – С дискретной передаточной функцией, включающей передаточную функцию экстраполятора;
3 - Непрерывная система с экстраполятором нулевого порядка с коэффициентом К, выводящий систему почти на границу устойчивости;
4 – Непрерывная система с экстраполятором нулевого порядка;
5 – Непрерывная система с экстраполятором и цифровым интегратором с коэффициентом К.
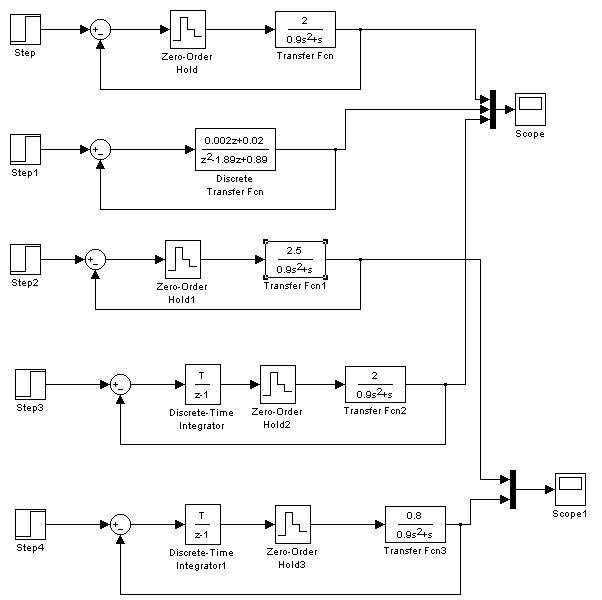
.
Рисунок 3 – Модели ЛИС
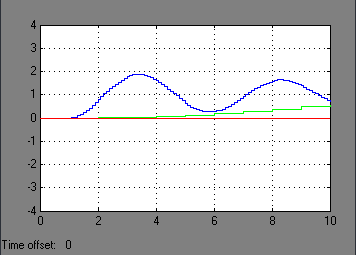
Рисунок 4 – Переходные характеристики систем 1, 2, 4
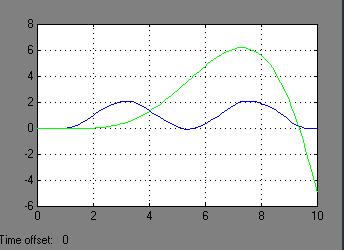
Рисунок 5 – Переходные характеристики систем 3,5
Вывод: в ходе лабораторной работы было исследовано влияние параметров ЛИС на устойчивость и качество переходных процессов.
