ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ»

Кафедра технологии металлов

и ремонта машин

Опд.Ф.07 метрология, стандартизация и сертификация Методические указания к выполнению курсовой работы

Направление подготовки дипломированных специалистов

110300 - Агроинженерия

Специальность 110302 – Электрификация и автоматизация

сельского хозяйства

Уфа 2010

УДК 378:389.16

ББК 74.58.30.10

Утверждено на заседании кафедры технологии металлов и ремонта машин. Протокол № ___ от « ___» _________ 2010 г. Рекомендовано к изданию методической комиссией энергетического факультета Протокол № ___ от «___» ________20____ г.

Составитель: канд. техн. наук, доцент Гаскаров И.Р.

Рецензент: канд. техн. наук, доцент Галимарданов И.И.

Ответственный за выпуск заведующий кафедрой технологии металлов и ремонта машин Фаюршин А.Ф.

Введение

Метрология, стандартизация и сертификация являются инструментами обеспечения качества продукции, работ и услуг – важнейшего аспекта многогранной коммерческой деятельности.

Проблема качества актуальна для всех стран независимо от зрелости их рыночной экономики. Изготовитель и его торговый посредник, стремящиеся поднять репутацию торговой марки, победить в конкурентной борьбе, выйти на мировой рынок, заинтересованы в выполнении как обязательных технических регламентов, так и рекомендуемых требований стандартов.

Стандартизация обеспечивает не только конкурентоспособность, но и эффективное партнерство изготовителя, заказчика и продавца на всех уровнях управления. Сегодня поставщику недостаточно строго следовать требованиям прогрессивных стандартов – надо подкреплять выпуск товара и оказания услуг сертификатом безопасности или качества.

Соблюдение правил метрологии в различных сферах коммерческой деятельности (торговле, банковской деятельности и пр.) позволяет свести к минимуму материальные потери от недостоверных результатов измерений.

Мероприятия по обеспечению единства измерений и требуемой точности измерений установлены законодательно.

Очень строго стоит вопрос о гармонизации отечественных правил стандартизации, метрологии и сертификации с международными правилами, поскольку это является важным условием вступления России во Всемирную торговую организацию (ВТО) и дальнейшей деятельности страны в рамках этой организации.

Таким образом, переход страны к рыночной экономике с присущей ей конкуренцией, борьбой за доверие потребителя заставит специалистов шире использовать методы и правила стандартизации, метрологии и сертификации в своей практической деятельности для обеспечения высокого качества товаров, работ и услуг.

1 Обработка результатов прямых измерений с многократными наблюдениями

При статистической обработке группы результатов наблюдений, объемом х₁,х₂,…,х_n следует выполнить следующие операции /1/:

1) Вычислить среднее арифметическое результатов наблюдений, принять его за результат измерения

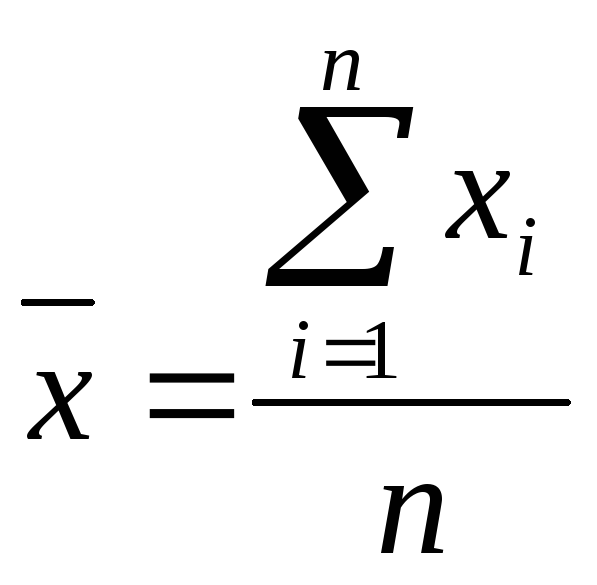; (1.1)

2) Вычислить оценку среднего квадратического отклонения ряда измерений (результатов наблюдений, метода измерений)

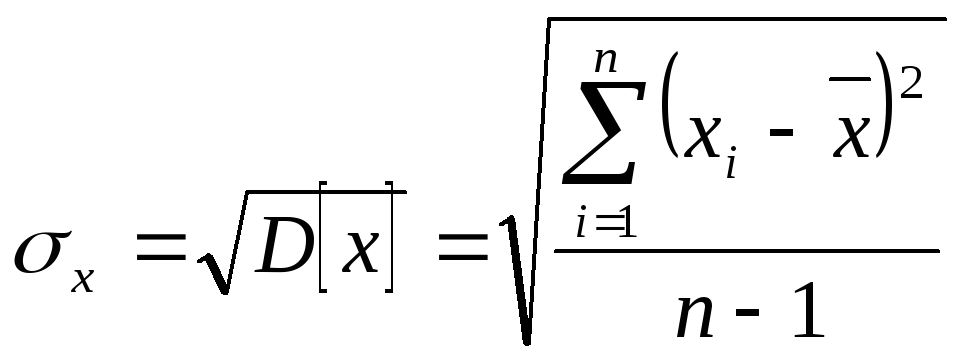; (1.2)

3) Проверить результаты наблюдений на наличие промахов. Можно использовать любой из известных критериев. При выявлении промахов исключить их из результатов наблюдений и заново определить результат измерения и оценку среднего квадратического отклонение по формулам 1.1 и 1.2.

4) Вычислить оценку среднего квадратического отклонения результата измерений

; (1.3)

5) Вычислить границы неисключенной систематической погрешности результата измерения

(1.4)

6) Представить результаты прямых многократных наблюдений, используемые в дальнейшей обработке результата косвенного измерения и анализе погрешностей, в форме:

(1.5)

7) Представить результаты прямых многократных наблюдений с учетом суммарной составляющей погрешности, как систематической, так и случайной составляющих с доверительными границами 0,

7.1) Определение доверительных границ неисключенных систематических погрешностей (НСП) результата измере­ния

При тщательной попытке исключить систематическую состав­ляющую погрешности какая-то часть ее все равно останется неисключённой. Доверительную границу НСП можно вычислить в результате анализа условий проведения эксперимента (например, неисключенная погрешность метода измерения, пределы допускаемой погрешности и пределы дополнительных погрешностей для средства измерения, погрешность округления результатов, погрешность отсчета и т. д.).

Неисключенные систематические погрешности рассматриваются как реализации случайной величины, имеющей равномерное распределение.

Каждая из НСП имеет свою границу Если значения Θ_i - существенно отличаются друг от друга (например, на два порядка или еще больше), то меньшие из них следует отбросить, а оставшиеся просуммировать с учетом вероятностного коэффициента К по формуле

(1.6)

где - граница i-й неисключенной систематической погрешности, найденная нестатистическими методами;

m - число составляющих НСП;

К - коэффициент, определяемый принятой доверительной вероятностью и числом составляющих НСП m.

При Р = 0,9 К =0,95; при Р = 0,95 К = 1,1 при любом значении m.

При Р = 0,99 значения К при различном значении m определяют по таблице 1.1.

Таблица 1.1 Значения коэффициента К для определения доверительных границ НСП при Р =0,99

m	≥5	4	3	2
К	1,45	1,40	1,30	1,20

1. Определение доверительных границ случайной составляющей погрешности результата измерения

При малом числе наблюдений n < 20 доверительный интервал случайной погрешности находят с помощью нормированного распределения Стьюдента по формуле

(1.7)

где t – коэффициент Стьюдента, выбираемый в зависимости от принятой доверительной вероятности Рд и числа наблюдений n.

Значения коэффициентов t распределения Стьюдента в зависимости от принятой доверительной вероятности Рд и числа степеней свободы (n – 1) при малом числе наблюдений n приведены в таблице 1.2.

Таблица 1.2. Коэффициенты t распределения Стьюдента

Рд	Число степеней свободы (n – 1)
	3	4	5	6	8	9	10	12
0,90	2,35	2,13	2,1	1,94	1,86	1,83	1,81	1,78
0,95	3,18	2,70	2,57	2,45	2,31	2,27	2,23	2,18
0,99	5,84	4,60	4,03	3,71	3,36	3,25	3,17	3,06

2. Определение доверительных границ общей (суммарной) погрешности результата измерения

Доверительные границы общей погрешности результата косвенного измерения определяются по композиции законов распределения случайной и неисключенной систематической составляющих погрешности в зависимости от значения отношения между систематической и случайной составляющими погрешности.

Если 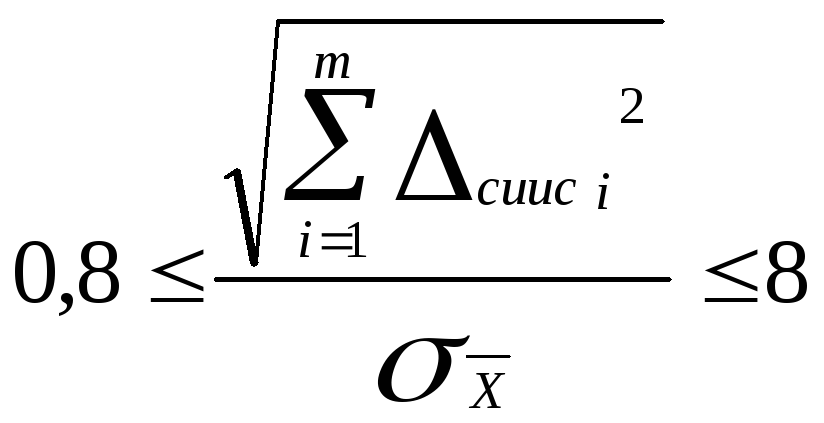, то суммарная погрешность вычисляется как

(1.8)

где – коэффициент распределения композиции случайной и неисключенной систематической погрешностей результата косвенных измерений при заданной доверительной вероятности РД

- оценка суммарного среднего квадратического отклонения композиции указанных законов распределения.

Формулу (1.8) можно использовать в соответствии с ГОСТ 8.207 при условии, что неисключенные систематические погрешности аргументов измерений распределены по равномерному закону, а случайные погрешности по нормальному закону.

Коэффициент вычисляют по эмпирической формуле

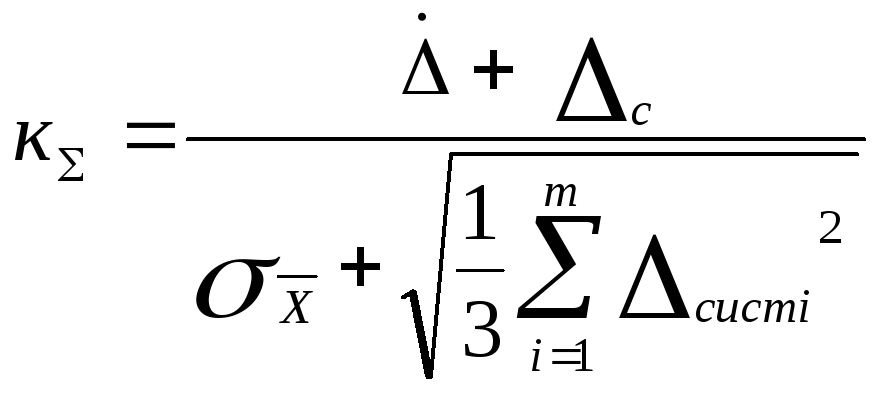. (1.9)

Оценку суммарного среднего квадратического отклонения результата измерения вычисляют по формуле

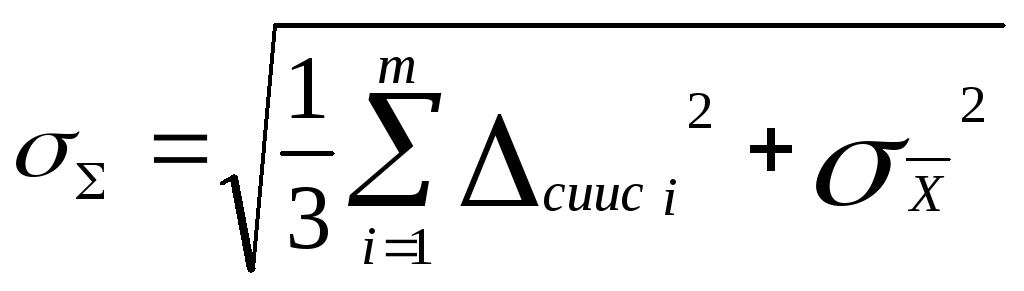. (1.10)

Если 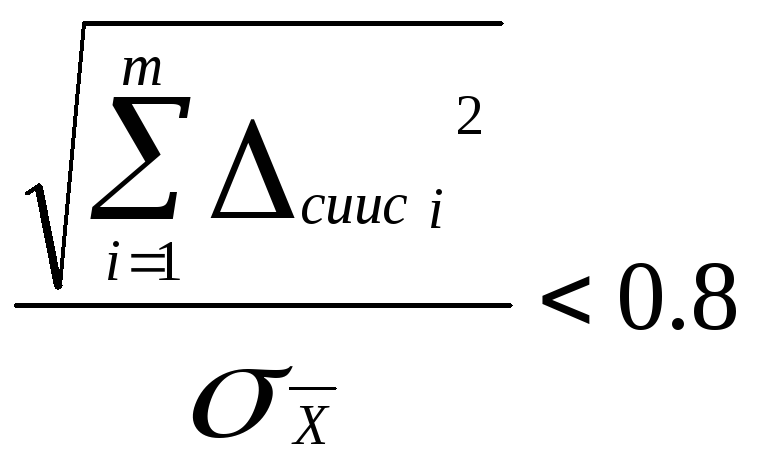, то неисключенной систематической погрешностью по сравнению со случайными пренебрегают и принимают, что граница погрешности результата

(1.11)

Если 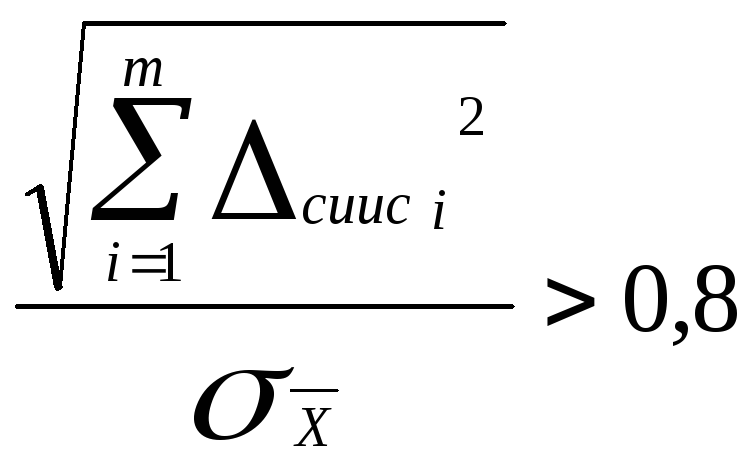, то случайной погрешностью по сравнению с неисключенной систематической погрешностью пренебрегают и принимают что граница погрешности результата

(1.12)

Результат измерения привести в виде

(1.13)