Вопросы к теоретическому зачету по математическому анализу.

Часть 1. Определение и арифметические свойства производной.

1. Определение производной функции в точке. Понятие дифференцируемости функции в точке и на промежутке.

2. Геометрический и физический смысл производной. Понятие касательной. Уравнение касательной.

3. Связь понятий дифференцируемости и непрерывности.

4. Формулы, выражающие связь понятий предела и производной.

5. Производные элементарных функций.

6. Производная суммы и разности.

7. Производная произведения.

8. Производная сложной функции.

9. Производная частного.

10. Производная обратной функции (без доказательства).

Часть 2. Французские теоремы и исследование функций с помощью производной.

1. Локальный экстремум функции и теорема Ферма.

2. Следствие о точках подозрительных на экстремум.

3. Теорема Ролля.

4. Следствие о количестве решений «производного уравнения».

5. Теорема Лагранжа.

6. Дифференциальный критерий монотонности (следствие теоремы Лагранжа).

7. Теорема Коши.

8. Правило Лопиталя.

9. Определение выпуклой функции. Критерий выпуклости в терминах первой производной.

10. Критерий выпуклости в терминах второй производной. Точки перегиба.

11. Неравенство Йенсена.

12. Теоремы о числе решений уравнений с частями разной выпуклости.

13. Теорема о знаке разности функций разной выпуклости.

14. Асимптоты. Расположение графика функции относительно асимптоты.

Материал для справок. Часть 2.

1. Локальный экстремум и теорема Ферма.

Определение. Пусть – некоторая функция с областью определения . Точка называется точкой локального максимума функции , если существуют такие и , что для всех , лежащих в , справедливо неравенство .

Аналогично определяется точка локального минимума функции . Точка называется точкой локального экстремума функции , если она является для нее точкой локального максимума или локального минимума. Если в какой-то точке функция принимает наибольшее на всей области определения значение, то эту точку называют точкой глобального максимума для функции. Очевидное определение имеют также понятия глобального минимума и глобального экстремума. Ясно, что точка глобального максимума функции является также и точкой ее локального максимума, но не наоборот.

Пример: Пусть . Тогда точка является для точкой локального максимума, поскольку для любого справедливо соотношение . В то же время наибольшего значения на всей области определения и, тем самым, точки глобального максимума, функция не имеет.

Теорема Ферма. Пусть R, и – точка локального экстремума функции . Пусть дифференцируема в точке . Тогда .

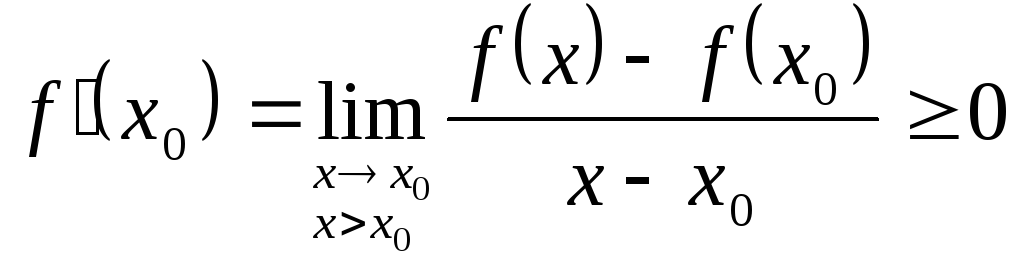Доказательство. Предположим, что имеет в точке локальный максимум, то есть существуют такие и из , что и для всех . Тогда при всех , а дробь , соответственно, неотрицательна при и неположительна при . Следовательно, с одной стороны, , с другой стороны, 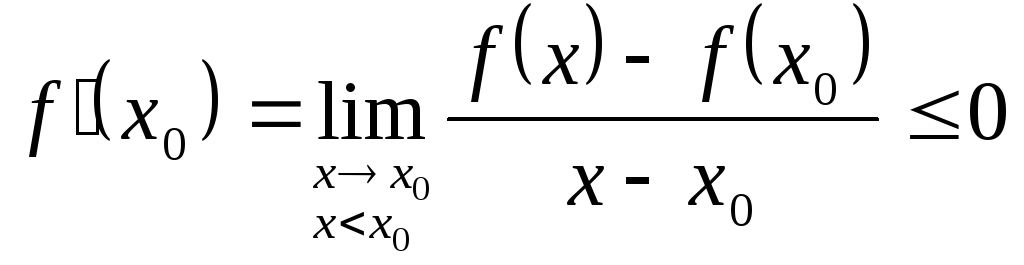, и, значит, .

2. Следствие о точках подозрительных на экстремум.

Пусть R, . Точка называется критической точкой функции , если дифференцируема в точке и . Точка называется точкой недифференцируемости функции , если в точке функция не имеет конечной производной (иначе говоря функция не является дифференцируемой в этой точке).

Предложение (следствие теоремы Ферма). Пусть R, . Тогда функция может иметь экстремум в точке только, если – критическая точка функции , или - точка недифференцируемости функции , или совпадает с одним из концов промежутка .

Доказательство. Утверждение предложения означает, что если не является концом промежутка и точкой недифференцируемости для , но является точкой локального экстремума, то тогда обязана быть критической точкой функции , то есть . Последнее верно по теореме Ферма.

Замечание 1. Критические точки, точки недифференцируемости и концы промежутка вместе называют точками, подозрительными на экстремум для функции . Из приведенного выше предложения вытекает, что наибольшее и наименьшее значение функция на промежутке может принимать только в одной из точек, подозрительных на экстремум.

Замечание 2. Если функция непрерывна на замкнутом промежутке , то она обязательно принимает в одной из точек этого промежутка наибольшее значение. Это утверждение называется «теоремой Вейерштрасса», как и аналогичное утверждение о наименьшем значении. Если , то есть промежуток не замкнут, то наибольшего и наименьшего значения функции на может и не быть.