- •Операторный метод анализа линейных систем. Введение. Основные понятия теории управления.
- •Операторный метод анализа линейных систем.
- •Описание элементов системы.
- •Уравнения элементов.
- •Передаточная функция.
- •Весовые и переходные функции звена.
- •Характеристики типовых звеньев.
- •Описания систем.
- •Структура и структурная схема системы.
- •Соотношения «вход - выход».
- •2. Структурные представления.
- •Устойчивость.
- •Устойчивость звена по входу.
- •Алгебраические критерии устойчивости.
- •Устойчивость по начальным условиям.
- •4. Устойчивость системы.
- •Установившаяся реакция и частотная характеристика.
- •Определение реакции при гармоническом воздействии.
- •Анализ типовых структур.
- •Соединения с отрицательной обратной связью.
- •Обобщенный критерий Найквиста.
-
Обобщенный критерий Найквиста.
Сформулированный достаточные условия не дают ответа на вопрос: может ли система с обратной связью быть устойчивой, если характеристические многочлены звеньев имеют корни в правой полуплоскости (т.е. заведомо неустойчивые). Оказывается это возможно и существует необходимое и достаточное условие устойчивости такой системы.
Теорема 1.5.2.(Обобщенный критерий Найквиста).
Пусть выполнены условия:
-
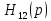 -
правильная дробно-рациональная функция;
-
правильная дробно-рациональная функция; -
Многочлены
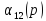 и
и
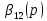 не имеют совпадающих корней в правой
полуплоскости (нули и полюса
не имеют совпадающих корней в правой
полуплоскости (нули и полюса
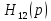 - не совпадают;
- не совпадают; -
Известно число полюсов
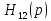 в правой полуплоскости равно q.
в правой полуплоскости равно q.
Тогда
для устойчивости системы звеньев с
отрицательной связью необходимо и
достаточно чтобы при
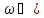 точка
точка
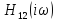 на комплексной плоскости совершала,
ровно q
полуоборотов
вокруг критической точки (-1;0) или, что
то же самое, годограф
на комплексной плоскости совершала,
ровно q
полуоборотов
вокруг критической точки (-1;0) или, что
то же самое, годограф
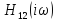 ровно q/2
раза охватывает критическую точку.
ровно q/2
раза охватывает критическую точку.
Вместо доказательства: геометрические примеры:
Следствие
1.
Оба звена устойчивы, т.е.
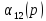 -
устойчиво.
-
устойчиво.
-
Пересекает правее (-1,0). (Может и вовсе не пересекать!).
I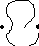
-1 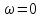 R
R
-
Столько раз пересекает ось по направлению вверх, сколько и по направлению вниз.
I
-1
 R
R
В
этих случаях годограф
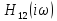 не
должен
охватывать (-1,0). Эта ситуация соответствует
ранее разобранной теореме 1.5.1.
не
должен
охватывать (-1,0). Эта ситуация соответствует
ранее разобранной теореме 1.5.1.
Следствие
2.
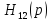 не имеет полюсов на мнимой оси, но есть
не имеет полюсов на мнимой оси, но есть
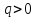 полюсов справа.
полюсов справа.
Пусть
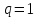 .
Тогда если годограф такой же, как на 1)
или 2), то теперь система
неустойчива,
а вот если, то соответственно неустойчивая
система (один полуоборот).
.
Тогда если годограф такой же, как на 1)
или 2), то теперь система
неустойчива,
а вот если, то соответственно неустойчивая
система (один полуоборот).
I
-1 R
Следствие
3.
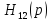 имеет 1 нулевой корень, а остальные корни
– слева.
имеет 1 нулевой корень, а остальные корни
– слева.
В
этом случае кривая строится без
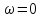 (т.к. тогда
(т.к. тогда
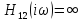 ).
).
-
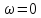 I
I
-1 R
I
-1 R
Более
сложные случаи, когда
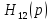 имеет кратные корни, рассматривать не
будем, т.к. в этих случаях могут возникнуть
разрывы графика годографа
имеет кратные корни, рассматривать не
будем, т.к. в этих случаях могут возникнуть
разрывы графика годографа
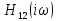 и требуется специальная процедура их
дополнения (см. учебник).
и требуется специальная процедура их
дополнения (см. учебник).
Лабораторная работа:
-
Выбрать 2 случая
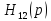 :
:
-
С полюсами только слева;
-
С несколькими (1,2) полюсами справа.
-
Построить годограф
 и по графику, следуя теоремам 1.5.1 и
1.5.2 определить устойчивость системы с
отрицательной обратной связью.
и по графику, следуя теоремам 1.5.1 и
1.5.2 определить устойчивость системы с
отрицательной обратной связью.