
- •Операторный метод анализа линейных систем. Введение. Основные понятия теории управления.
- •Операторный метод анализа линейных систем.
- •Описание элементов системы.
- •Уравнения элементов.
- •Передаточная функция.
- •Весовые и переходные функции звена.
- •Характеристики типовых звеньев.
- •Описания систем.
- •Структура и структурная схема системы.
- •Соотношения «вход - выход».
- •2. Структурные представления.
- •Устойчивость.
- •Устойчивость звена по входу.
- •Алгебраические критерии устойчивости.
- •Устойчивость по начальным условиям.
- •4. Устойчивость системы.
- •Установившаяся реакция и частотная характеристика.
- •Определение реакции при гармоническом воздействии.
- •Анализ типовых структур.
- •Соединения с отрицательной обратной связью.
- •Обобщенный критерий Найквиста.
-
Характеристики типовых звеньев.

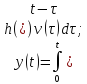

-
Идеальный усилитель
 (1.11);
(1.11);
-
Интегратор
 (1.15);
(1.15);
-
Апериодическое звено
 (1.16);
(1.16);
-
Колебательное звено
 при
0<k<1
(1.17)
при
0<k<1
(1.17)
-
Идеальный усилитель
 (1.11)
(1.11)
Рассмотрим
 -
дельта функция Дирака.
-
дельта функция Дирака.
Пусть
δ*(t,
a)
=
 ;
и тогда
;
и тогда
 – импульсная
функция;
– импульсная
функция;


а
Найдем
изображение по Лапласу от
 :
:


 (при
(при
 )
)
1 = ℒ(δ(t)) (1.12).
Определим
теперь
 весовую функцию из равенства:
весовую функцию из равенства:

В
изображениях:
 ,
значит
,
значит
 ;
;
 ;
;
Получим,
что весовая функция
 ; (1.13)
; (1.13)
Найдем теперь:
 ;
;
Перейдем к изображениям:
 ,
,
Докажем,
что: .
.

Следовательно:

Одновременно
установлено соотношение между
 и
и .
.
 и
и
 (1.14)
(1.14)
 ,
a
,
a
 .
.
-
Интегратор
 (1.15);
(1.15);
Звено
осуществляет интегрирование входного
сигнала к
 (1.15’)
(1.15’)
В
изображениях по Лапласу:
 ;
;
 ,
,
 ,
,
Тогда
 определяет
определяет
 ,
,
Следовательно
 .
.
 .
.
-
Апериодическое звено
 (1.16);
(1.16);
В изображениях по Лапласу:
 =>
=>
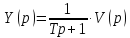 ,
,
 – передаточная
функция.
– передаточная
функция.
 ;
по теореме смещения:
;
по теореме смещения:
 ;
значит
;
значит
 -это
весовая функция апериодического звена.
-это
весовая функция апериодического звена.
 ;
;
 (1.16’)
(1.16’)
-
Колебательное звено
 при
0<k<1
(1.17)
при
0<k<1
(1.17)
 выбирается
чтобы характеристическое уравнение
имело только комплексные корни.
выбирается
чтобы характеристическое уравнение
имело только комплексные корни.
 ;
0<k<1;
;
0<k<1;
 ;
;

Где
 ,
,
 .
.
Найдем
весовую функцию
 :
:
 ;
;
 ;
;
 ;
;
Тогда
 ;
;
 .
.
Теперь
положим
 ,
тогда
,
тогда
 ;
;
 ;
;
 ;
;
 .
.
Воспользуемся теоремой о смещении:
 ;
;
 (1.17)
(1.17)
Т.к.
 ,
то имеем:
,
то имеем:
h(t)
 .
.
Найдем теперь
 ;
;
 .
.
-
Описания систем.
-
Структура и структурная схема системы.
Перейдем к описанию систем, состоящих из взаимосвязанных звеньев. Для i-го звена:
вход
 ,
выход
,
выход
 и тогда:
и тогда:
 (2.1)
(2.1)
 (2.2)
(2.2)
Взаимосвязь между звеньями:
 или
в более общем виде:
или
в более общем виде:

Где
 - внешнее воздействие не связанное с
системой на i-ое
звено,
- внешнее воздействие не связанное с
системой на i-ое
звено,
 ,
,
0 – если к-ое звено не связано с i-ым;
1 – в зависимости от знака воздействия к-го звена на i-ое .
Определение:
число
не нулевых
 называется плотностью
связи
i-го
звена.
называется плотностью
связи
i-го
звена.
Если плоскость невелика, то удобно использовать описание с помощью структурных схем, использующих язык теории графов. Каждое звено – прямоугольник, входное воздействие (->) в него, выходное (->) из него. Внутри прямоугольника или номер, или переходная функция. Операторы суммирования – изображены кругом, причем при отрицательной связи, около стрелки ставится (-).
Пример структурной схемы:








Запишем систему в виде уравнений:

 .
.
-
Соотношения «вход - выход».
При
изучении систем чаще всего интересует
значение связи между внешними входами
и выходами звеньев. Эти связи легче
устанавливаются, если перейти к
 - образам.
- образам.
Тогда, при нулевых начальных условиях, получаем:


Это
С.Л.А.У. с помощью, которой можно неизвестные
 выразить через
выразить через
 - образы внешних входов
- образы внешних входов
 .
Рассмотрим пример, как реальное
физическое устройство может быть изучено
по предложенной выше схеме.
.
Рассмотрим пример, как реальное
физическое устройство может быть изучено
по предложенной выше схеме.
Пример:
электромотор редуктор

 ротор
вал
ротор
вал

Запишем все основные соотношения из электричества и динамики (ТМ) для объектов этой системы
-
 -
подается из преобразователя информации
на усилитель и образуется
-
подается из преобразователя информации
на усилитель и образуется

Напряжение,
 подаваемое на электродвигатель
постоянного тока.
подаваемое на электродвигатель
постоянного тока.
-
Известно, что если
 - индуктивность обмоток ротора,
- индуктивность обмоток ротора,
 - сопротивление цепи ротора, то формируется
сила тока
- сопротивление цепи ротора, то формируется
сила тока
 связана
с подаваемым напряжением
связана
с подаваемым напряжением
 следующим
образом:
следующим
образом:
 ,
,
где
 - противоЭДС возникающее из-за индуктивности
катушки;
- противоЭДС возникающее из-за индуктивности
катушки;
D-дифференциальный оператор.
 ,
,
где
 -угловая
скорость;
-угловая
скорость;
 – коэффициент.
– коэффициент.
-
Известно также, что момент ротора
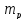 пропорционален возникающей в его цепи
силе тока
пропорционален возникающей в его цепи
силе тока
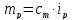
-
Теперь необходимо записать известные из ТМ уравнения движения (вращения) оси ротора и вала нагрузки. При этом надо учитывать передающееся через редуктор момент на вал нагрузки
 и обратно – момент противодействия
нагрузки на ось ротора
и обратно – момент противодействия
нагрузки на ось ротора
 .
Если r
– коэффициент редуктора, то тогда
.
Если r
– коэффициент редуктора, то тогда
 и точно также связаны углы поворота и
углы скорости оси ротора
и точно также связаны углы поворота и
углы скорости оси ротора
 ,
,
 и вала нагрузки
и вала нагрузки
 и
и
 .
.



-
Записываем уравнение динамики вращательного движения:
 -
для ротора
-
для ротора
 -
для вала
-
для вала
( - внешний момент, приложенный к валу)
- внешний момент, приложенный к валу)
Исключим
из этих уравнений

 =
=
 =
=
 .
.
Теперь
все соотношения можно изобразить в виде
структурной
схемы:

(-)

 ip
ip


(-)


Самостоятельная
работа.
Как правило, не используется модель
абсолютной жесткости редуктора, тогда
вместо
 ,
вводим нагрузки
,
вводим нагрузки
 – т.е. момент редуктора пропорционален
разности углов поворота. При этом
сохраняется
– т.е. момент редуктора пропорционален
разности углов поворота. При этом
сохраняется
 .
.
Задание: изменить соотношения и составить новую структурную схему.
Найдем
теперь зависимость в виде формулы угла
поворота
 от внешних входов
от внешних входов
 и
и
 .
Все ранее встречаемые уравнения запишем
в образах по Лапласу (аргумент)
.
Все ранее встречаемые уравнения запишем
в образах по Лапласу (аргумент)

 ,
,
 ,
,
 ,
,
 .
.
Осталось
исключить
 .
.


Раскрываем
скобки и находим
 .
.

Получить
аналогичную зависимость
 от
от
 и
и
 для случая упругого редуктора.
для случая упругого редуктора.
Найдем
теперь явную зависимость угла поворота
вала
 от внешних входов
от внешних входов
 и
и
 .
Для этого все уравнения (П 1.) перепишем
в
.
Для этого все уравнения (П 1.) перепишем
в
 - образах( аргумент р
– опускается, переходим к большим
буквам).
- образах( аргумент р
– опускается, переходим к большим
буквам).
 (П
1.2.3’)
(П
1.2.3’)
 (П
1.1)
(П
1.1)
 (П
1.9)
(П
1.9)
(П
1.3)
 ,
но из (П 1.6)
,
но из (П 1.6)
 ,
а из (П 1.8.8’)
,
а из (П 1.8.8’)
 ;
тогда:
;
тогда:
 (П
1.10)
(П
1.10)
(П
1.4)
 ,
,

 (П
1.11)
(П
1.11)
Система
( П 1.9,10,11) – это система из которой
исключением
 и
и
 можно найти выражение
можно найти выражение
 через
через
 и
и
 .
.
Сначала
исключим

(П
1.9)

Теперь
исключим из (П 1.11) и (П 1.12)
 и получим:
и получим:
 (П
1.13),
(П
1.13),
где
 и
и
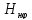 - дробно-рациональные функции. В
знаменателях, которых – многочлен 4-ой
степени, числитель
- дробно-рациональные функции. В
знаменателях, которых – многочлен 4-ой
степени, числитель
 ,
а числитель
,
а числитель
 - многочлен 3-ей степени (получить
самостоятельно).
- многочлен 3-ей степени (получить
самостоятельно).
Эти
соотношения упрощаются, если
 ,
(абсолютно жесткий редуктор), тогда:
,
(абсолютно жесткий редуктор), тогда:


где
 ;
;
 .
.
Если
кроме того пренебречь самоиндукцией
цепи ротора
 ,
то получим передаточную функцию совсем
простого вида:
,
то получим передаточную функцию совсем
простого вида:


Запишем в общем виде правила решения С.Л.А.У в изображениях.
Пусть система состоит из N звеньев, тогда:
 (2.6)
(2.6)

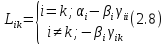
Применяя к (2.7) правило Крамера:
 (2.9)
(2.9)
 – определитель
системы (2.7)
– определитель
системы (2.7)
Т.к.
(2.8) относительно
 обычное СЛАУ, тогда введем такие
обозначения:
обычное СЛАУ, тогда введем такие
обозначения:

 -
алгебраическое дополнение к-го элемента
i-го
столбца той же матрицы.
-
алгебраическое дополнение к-го элемента
i-го
столбца той же матрицы.
Обозначим:
 (2.10)
(2.10)
 ;
(2.11)
;
(2.11)
Определение:
 назовем переходной
функцией
от к-го внешнего вход к i-мн
выходн. Используя теорему о ввертке:
назовем переходной
функцией
от к-го внешнего вход к i-мн
выходн. Используя теорему о ввертке:

 – весовые
функции, соотв.
– весовые
функции, соотв.
 .
.
Все переходные функции – дробно-рациональные функции.
 -
характеристический многочлен системы
-
характеристический многочлен системы
 .
.
Путь
 -внешний
выход системы.
-внешний
выход системы.
Тогда :

Где
 -
переходные функции внешнего входа к
внешнему выходу, тогда, запишем (2.12) в
виде:
-
переходные функции внешнего входа к
внешнему выходу, тогда, запишем (2.12) в
виде:

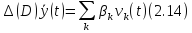
Приведем пример перехода от исходного описания к 1 дифференциальному уравнению.
Пример: рассмотрим систему, состоящую из 2-х звеньев.






Переходим к

Сокращаем на D-1.
Если сократить, то получим:

Если не сокращать, то получим:

Возникает
проблема: когда модели А и В эквивалентны.
Очевидно, условием эквивалентности
является условие существования обратного
оператора
 .
.
Условием существования обратного оператора является то, что оператор имеет нулевое ядро. Тогда это ядро f можно определить решив уравнение:


Тогда решением дифференциального уравнения будет:

Тогда f = 0, если c = 0 значит, ядро будет нулевым при начальных условиях f(0)=0.
Модели А и В эквивалентны только для нулевых начальных условий. Тогда решения А и В будут одинаковыми.
Вывод: работая с аналогом дифференциальных операторов: степенями p ненужно забывать о необходимости при сокращении обратных операторов сокращенных выражений.
