2. Передаточная функция.

Можно записать (1.2) в следующей форме:

y (t) = H (D) v (t),

где H(D) – дробно - рациональная функция от D.

H (D) = 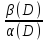– операторная передаточная функция.

Пока такая запись – символьная, т.к. не определено деление на операторный многочлен.

Пусть функция f(t), t>0, кусочно-непрерывная. Тогда ей можно поставить в соответствии:

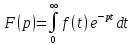
Такая F(p) называется преобразованием Лапласа от f(t).

;

;

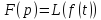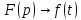f (t) должно быть таким, чтобы:

Оказывается что такое преобразование очень удобно для решения дифференциальных уравнений т.к. легко показать что:

Теорема 1.1:Если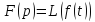, то

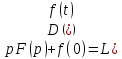
Доказательство:

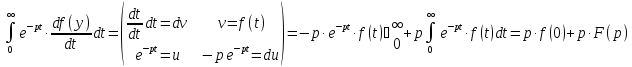
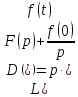(1.3)

Если f(0) = 0, то тогда операция дифференцирования в оригиналах заменяется в пространстве изображений по Лапласу умножением изображения F(p) на p при нулевых начальных условиях.

Точно также можно рассмотреть преобразование Лапласа от производных n-го порядка.

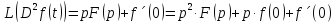
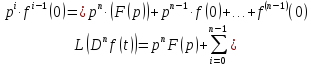(1.4)

Значит, если предположить, что функция f и все ее n-1 производная в нуле равны нулю, то:

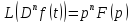(1.4´)

Применяя такое преобразование к (1.1.1) получим:

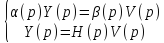(1.4’’)

3. Весовые и переходные функции звена.

Чтоб получить решение в оригиналах из (1.5) нужно применить обратное преобразование по Лапласу.

1. Свойства преобразования Лапласа

Так как в изображения имеется

Y (p) =H (p) ∙V (p), то очевидно что задача перехода в оригиналы связана с применения к последней формуле обратного преобразования Лапласа. Однако для этого приходилось бы применить интегрирование в комплексную плоскость.

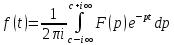
Можно поступить проще: для интересующих нас случаев можно использовать простые соотношения, вытекающие из нескольких теорем:

Теорема 1.2 (о смещении)

Если 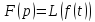преобразование Лапласа, то

F (p + a) =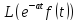 (1.5)

Смещение аргумента изображения на а приводит к умножению оригинала на .

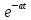Доказательство: По определению преобразования=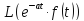

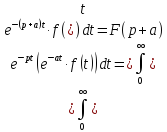
Теорема 1.3(запаздывания)

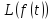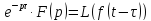Если F(p)= , то (1.6)

Умножение изображения на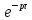 приводит в пространстве оригиналов к сдвигу аргумента на (-τ).

Доказательство:

т.к. по условию функция f обращается в ноль для отрицательного аргумента, а если 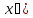, то

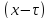отрицательна.

Теперь можно приступить к определению чему равняется оригинал от произведения изображений.

Определение: назовем сверткой двух функций f₁(t) и f₂(t) интеграл с переменным верхним пределом

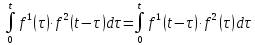
Теорема 1.4(о свертке)

Пусть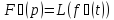и

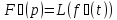
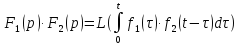(1.7)

Доказательство: Запишем для F₂(p) теорему 1.3. Т.е. :

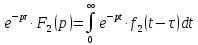(1.6)

Домножим слева и справа на f₁(τ) и проинтегрируем по τ от 0 до ∞, тогда:

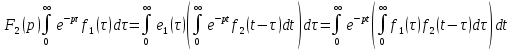
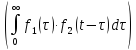– было бы сверткой, если б вместо ∞ в верхнем пределе было бы t, но т.к.

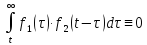т.е. подинтегральная функция (t-τ) отрицательна, то теорема доказана.

Ранее было введено понятие комплексной передаточной функции

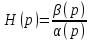
Теперь имеется возможность на основании доказанных во 2 пункте теорем перейти к оригиналам и получить зависимость y(t) через v(t). Воспользовавшись (1.7) можно записать

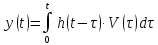(1.8) , что фактически является общим решением вырождающим выход звена y(t) через вход в звено v(t). Функция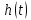 называется весовой функцией звена. Значит, задача сводится к построению по заданной весовой функции

В ТУ важное значение имеет реакция звена на так называемый единичный импульс.

Введем функцию Хэвисайда:

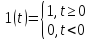
Пусть v(t) = 1(t)

Сначала найдем чему равно изображение по Лапласу от этой функции:

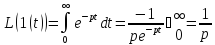
Определение: Назовемпереходной функцией:

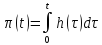(1.9)

Тогда получается что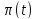это и есть реакция на 1(t).

Найдем теперь соотношение в изображениях между 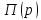и 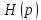, для этого докажем теорему:

Теорема 1.5: 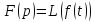тогда

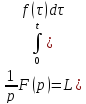
Преобразование Лапласа от интеграла с переменным верхним пределом от f(t)в пространстве изображений задает умножение F(p) образа на .

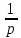Доказательство: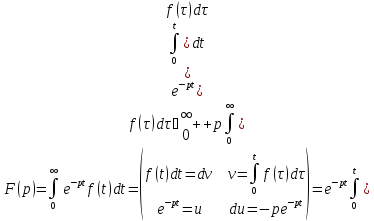

Тогда учитывая (1.9) находим, что 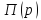= 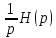(1.10) связь в изображениях между весовой и переходной функциями.

В ТУ классическими являются следующие звенья:

1. Идеальный усилитель;

2. Интегратор;

3. Апериодическое звено;

4. Колебательное звено.

Установим для всех таких типичных звеньев их характеристики H(p), h(t), π(t).