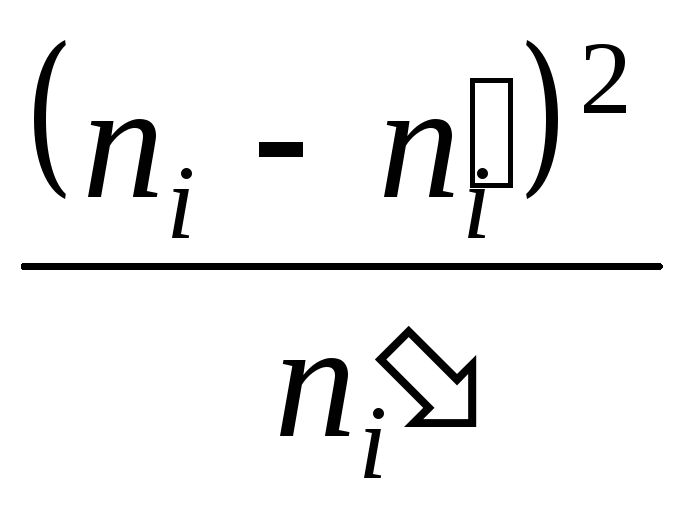Основные вопросы программы Математическая статистика

1. Генеральная и выборочная совокупности. Статистическое распределение выборки.

2. Дискретный и интервальный ряды распределения. Полигон и гистограмма.

3. Эмпирическая функция распределения и ее свойства.

4. Статистические оценки параметров распределения, требования к ним.

5. Генеральная и выборочная средняя, генеральная и выборочная дисперсии. Исправленная выборочная дисперсия.

6. Доверительный интервал для оценки математического ожидания нормального распределения.

7. Доверительный интервал для оценки среднего квадратического отклонения нормального распределения.

8. Статистическая проверка гипотез. Критерий согласия Пирсона.

9. Выборочный коэффициент корреляции. Уравнение линейной регрессии.

Задание 1

Пример. Даны результаты наблюдений некоторой случайной физической величины X, сгруппированные в интервальный статистический ряд

	3,45 ‑3,60	3,60 ‑3,75	3,75 ‑3,90	3,90 ‑4,05	4,05 ‑4,20	4,20 ‑4,35
ni	2	10	12	18	6	2

Требуется:

1. Построить гистограмму и полигон частот.

2. Составить эмпирическую функцию распределения и изобразить ее графически.

3. Вычислить числовые характеристики:

а) выборочную среднюю;

б) выборочное среднее квадратичное отклонение;

в) «исправленную» выборочную дисперсию и «исправленное» выборочное среднее квадратичное отклонение.

4. Определить точечные оценки параметров нормального закона распределения m и , предполагая, что исследуемая случайная величина распределена по нормальному закону; записать плотность распределения вероятностей f(х).

5. Найти теоретические частоты нормального закона распределения, проверить согласие эмпирической функции распределения с нормальным законом с помощью критерия Пирсона.

6. Найти интервальные оценки параметров нормального закона распределения (доверительную вероятность принять равной 0,99).

Решение.

1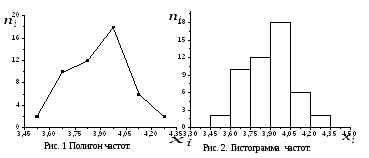) Графически данный ряд можно изобразить в виде полигона (рис. 1) и гистограммы частот (рис. 2). Для построения полигона частот в качестве вариант примем середины частичных интервалов, а в качестве частот – частоты интервала.

2) Найдем эмпирическую функцию распределения. Объем выборки n = 50. Наименьшая варианта равна 3,45, поэтому F(x) = 0 при х ≤ 3,45.

Значение случайной величины Х, меньшее 3,60, наблюдалось два раза, следовательно, F(x) = 2/50 = 0,02 при 3,45 < х ≤ 3,60.

Значение Х, меньшее 3,75, наблюдалось 2 + 10 = 12 раз; следовательно, F(x) = 12/50 = 0,24 при 3,60 < х ≤ 3,75.

Для значений Х, меньших 3,90; 4,05; 4,20 и 4,35, функция F(x) находится аналогично.

Поскольку значение Х, равное 4,35 – наибольшая варианта, то F(x) = 1 при x > 4,35.

Напишем искомую эмпирическую функцию распределения:

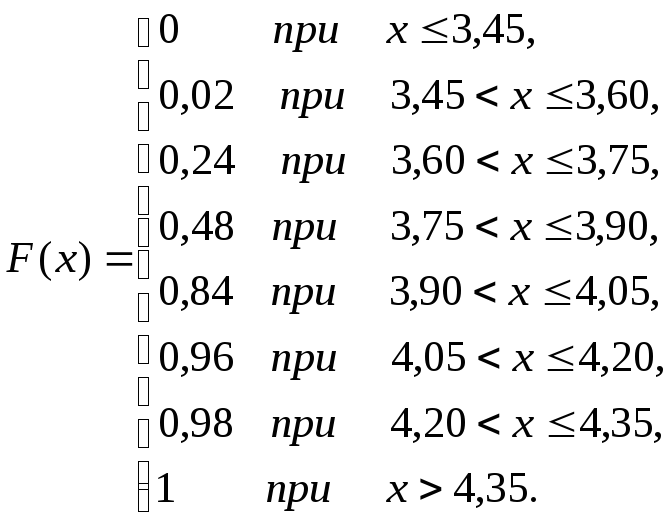
3) Выборочную среднюю найдем по формуле

,

где k – количество вариант.

При вычислении числовых характеристик случайной величины Х в качестве вариант будем принимать середины интервалов. Тогда

.

Для вычисления выборочного среднего квадратичного отклонения найдем сначала выборочную дисперсию по формуле

,

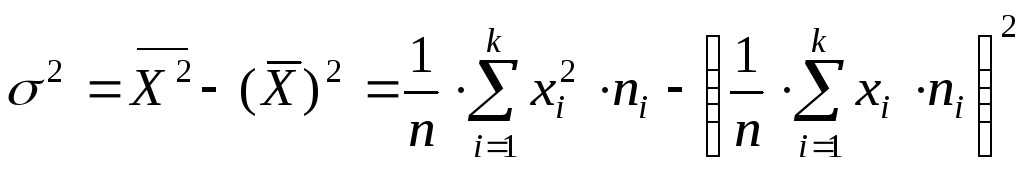где

.

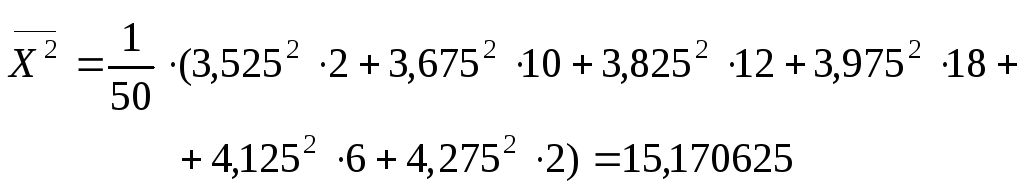Следовательно, = 15,170625 ‑ (3,891)² = 0,030744.

Тогда .

Несмещенной оценкой для дисперсии служит «исправленная» выборочная дисперсия:

,

а для среднего квадратичного отклонения несмещенной оценкой будет «исправленное» выборочное среднее квадратичное отклонение:

.

4) Пусть случайная величина Х распределена по нормальному закону. Тогда ее плотность распределения будет иметь вид

,

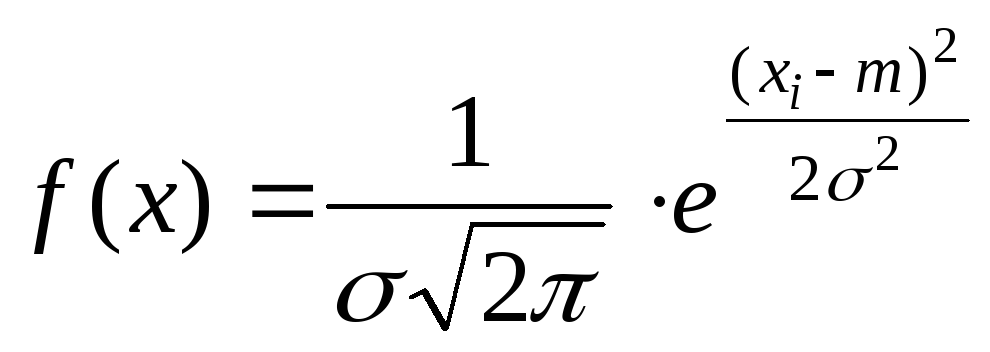где в качестве параметров распределения примем соответствующие несмещенные точечные оценки m = = 3,891 и  = s  0,175.

5) Найдем теоретические частоты. Для этого по формуле

вычислим вероятности p_i (i=1,2,…,6) того, что случайная величина Х содержится в интервале (х_i, x_i+1), а затем из соотношения найдем соответствующую теоретическую частоту случайной величиной Х в этом интервале:

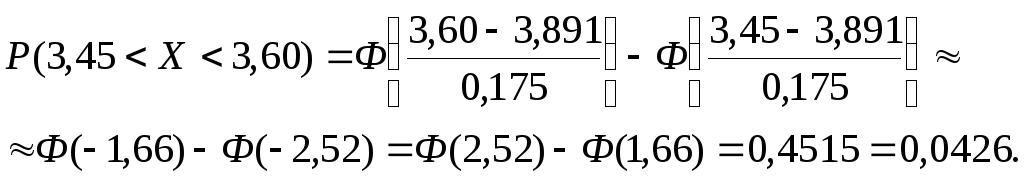
Отсюда p₁n = 0,042650 = 2,13, следовательно, (произведения p_in округляем до целых чисел).

Этим же способом находим и остальные теоретические частоты случайной величины Х:

р₂ = 0,1634, , р₃ = 0,3120, ,

р₄ = 0,2991, , р₅ = 0,1465, ,

р₆ = 0,0364, .

Для вычисления ² составим расчетную таблицу, при этом малочисленные эмпирические и соответствующие им теоретические частоты первых двух и последних двух групп таблицы соединим в две самостоятельные группы.

ni
12	10	2	4	0,4
12	16	-4	16	1
18	15	3	9	0,6
8	9	-1	1	0,11
Сумма 50				2,11

Следовательно,. По таблице вероятностей для критерия ², по уровню значимости =0,01 и числу степеней свободы k = s ‑ 3=1 (s = 4 – число интервалов) находим вероятность , так как при ² = 3 и k = 1 вероятность равна 0,0833, а при и при том же k = 1 вероятность  будет больше, чем 0,0833.

Таким образом, если уровень значимости  = 0,01, то полученная вероятность  больше, чем .

Итак, гипотезу о нормальном распределении случайной величины Х следует принять.

6) Интервальной оценкой (с уровнем доверия ) математического ожидания m нормально распределенной величины Х служит доверительный интервал

, (*)

где ‑ точность оценки, t – значение аргумента функции Лапласа , при котором .

Все величины, кроме t, известны. Определим t из соотношения . По таблице значений функции Лапласа находим t = 2,58. Подставив t = 2,58, , , n = 50 в (*), получим доверительный интервал 3,827 < m < 3,955.

Интервальной оценкой (с уровнем доверия ) среднего квадратического отклонения  нормально распределенной величины Х служит доверительный интервал

,

где s – «исправленное» выборочное среднее квадратическое отклонение, а q находят по таблице при заданных n и .

По данным  = 0,99 и n = 50 по таблице определим q = 0,3. Следовательно, доверительный интервал будет иметь вид

0,1240 <  < 0,2302.

Даны результаты наблюдений некоторой случайной физической величины X, сгруппированные в интервальный статистический ряд. В задачах 1.1. – 1.30: