12. Цепь переменного тока с емкостным сопротивлением.

Цепь с емкостью

Вели конденсатор емкостью С подключить к источнику с постоянным напряжением U (рис. 11.5а), то ток зарядки конденсатора проходит в цепи очень короткое время, пока напряжение на конденсаторе U_с не станет равным напряжению источника U.

Ток в рассматриваемой цепи (рис. 11.5а) практически отсутствует (амперметр А покажет I= 0).

Вели же конденсатор подключить к источнику с синусоидальном напряжением (рис. 11.56), то ток в цепи конденсатора существует все время, пока цепь замкнута, и амперметр А покажет этот ток. Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжение на конденсаторе U_c отстает по фазе от напряжения источника Ври зарядке, и при разрядке конденсатора. Например, пока напряжение на конденсаторе достигает значения 1, напряжение источника достигнет значения 2 (рис. 11.5в), т. е. конденсатор заряжается; пока конденсатор зарядится до напряжения 2, напряжение источника уменьшится до напряжения 3 – конденсатор разряжается на источник и т.д. Однако ток проходит только в цепи конденсатора. Через диэлектрик конденсатора ток не проходит.

Таким образом, если к конденсатору емкостью С приложено синусоидальное напряжение и= U_msinώt, то в цепи конденсатора проходит ток I (рис. 11.6а):

где q= Си согласно (6.3).

Очевидно, ток в цепи конденсатора достигает амплитудного значения тогда, когда

Тогда

Как видно, ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90° = π/2l

Следовательно, напряжение отстает по фазе от тока на 90° = π/2 (рис.11.66)

Если уравнение (11.17) разделить на √2 =1,41, то получится равенство I= UώC или

Это равенство (11.19а) и является математическим выражением закона Ома для цепи переменного тока с емкостью. Очевидно, знаменатель этого равенства является сопротивлением конденсатора Хс, которое называется емкостным сопротивлением:

Тогда закон Ома для цепи с конденсатором можно записать:

Емкостное сопротивление — это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему (рис. 11.5а).

12. Неразветвленная RL-цепь.

13. Неразветвленная RC-цепь.

14. Неразветвленная RLC-цепь.

40. Построение векторно-топографической диаграммы и нахождение по ней напряжений от­дельных участков.

41. Резонанс напряжений.

42. Расчет цепи, состоящей из параллельно включенных активного индуктивного и емкостно­го сопротивлений.

Неразветвленная цепь с активным сопротивлением, индуктивностью и емкостью

Если в неразветвленной цепи с R, L и С (рис. 12.4а) протекает синусоидальный ток i=I_msinώt, то он создает падение напряже­ния на всех участках цепи: u_а= U_masinώt, u_L= U_mLsin (ώt +π/2) и

u_с= U_msin(ώt-π/2).

Мгновенное значение напряжения цепи определяется по фор­муле

Так как в рассматриваемой цепи включены два реактивных со­противления X_L и Х_с, то возможны три режима работы цепи: l)X_L>X_c;2)X_L<X_c;3)X_L = Xc.

Векторная диаграмма цепи для режима X_L>Х_с изображена на рис. 12.46

Знак перед углом сдвига фаз φ зависит от режима работы цепи. Если в рассматриваемой цепи преобладает индуктивное напряжение (сопротивление), т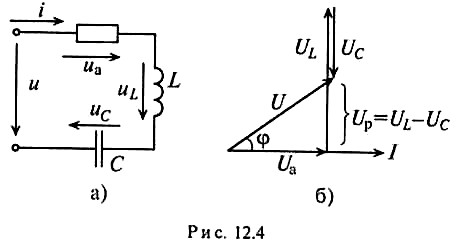.е. U_L> U_c, то цепь имеет индуктивный характер и напряжение U опережает по фазе ток I(+φ).

Если в цепи преобладает емкостное напряжение (сопротивление), т.е. U_L< U_c, то цепь имеет емкостной характер и напряже­ние U отстает по фазе от тока I(—φ) Из векторной диаграммы (рис. 12.46) следует

Сопротивление R может включать в себя сопротивление само­стоятельного резистора или активное сопротивление реальной катушки и конденсатора.

Математическое выражение закона Ома для неразветвленной цепи с активным сопротивлением, индуктивностью и емкость:

_Где Z — полное (или кажущееся) сопротивление неразветвлен­ной цепи с R, L и С, т. е.

На рис. 12.5 изображены треугольники напряжений, сопротив­лений и мощностей для рассматриваемой цепи.

Знак и значение угла φ можно определить из треугольника со­противлений (рис. 12.56):

Из выражений (12.20) и (12.21) видно, что если X_L>Х_с, то угол φ положителен (+φ), если X_L<X_C, то угол ф отрицательный (-φ).

Из треугольника мощностей (рис. 12.5в) видно, что в цепи с R, L и С кроме активной мощности P=Scosφ имеется реактивная мощность Q=S sinφ. Кроме того, в цепи происходит колебание мощности (меньшей из двух реактивных, в нашем случае U_c ) между электрическим полем конденсатора С и магнитным полем катушки индуктивности L, так как мощности Q_L и Q_c изменяются в противофазе. Но эта мощность (1—2 на рис. 12.5в) не считается реактивной, так как она не загружает источник и провода.

Из треугольника мощностей (рис. 12.5в) видно, что реактивная мощность, которая загружает источник и провода, Q= Q_L - Q_c. Эта реактивная мощность (энергия) колеблется между источ­ником и магнитным полем катушки индуктивности, так как Q_l>Q_c

Полная мощность цепи определяется по формуле

40. Расчет разветвленной цепи методом проводимостей.

41. Резонанс токов.

42. Значение коэффициента мощности в электроэнергетике.