лабораторная работа / МЕТОД ГАРМОНИЧЕСКОГО БАЛАНСА (2)

МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РФ

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

факультет: ИС

кафедра: УИТ

дисциплина: теория автоматического управления

МЕТОД ГАРМОНИЧЕСКОГО БАЛАНСА

Вариант №8

Выполнил:

студент 4-его курса

гр. УИТ-42

Есипов С.

принял:

Скоробогатова Т.Н.

г. Балаково 2006 г.

Цель работы: ознакомится с методами гармонической линеаризации нелинейностей и методами расчета параметров автоколебаний в нелинейных системах.

Структурная схема исследуемой системы:

Передаточная функция линейной части:

Зададим нелинейность типа «идеальное реле»:

Примем а=

Проведем анализ системы способом Гольдфарба.

1. На комплексной плоскости построим АФХ линейной части Wл(jw) и зависимость для нелинейной части: -. Для построения последней воспользуемся коэффициентами гармонической линеаризации для нелинейности типа «идеальное реле»:

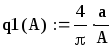
Получили графики:

Из координат точки пересечения находим:

-=-0.51; А=2.068;

Вывод: При движении по обратной частотной характеристике НЭ АФХ линейная часть пересекается изнутри наружу, поэтому система имеет устойчивые автоколебания с угловой частотой и амплитудой А=2.068

2. Зададим нелинейность типа «реле с гистерезисом»

Из пересечения графиков видно:

-=-0.63647-j0.78562, А=4

3.144

График пересекается изнутри наружу, поэтому автоколебания являются устойчивыми.