лабораторная работа / ТАУ - Расчетная работа 5

Министерство Образования Российской Федерации

Уфимский Государственный Авиационный Технический Университет

Кафедра ТК

Отчет по практической работе

по предмету «Основы теории управления»

Выполнила: студентка

гр.Т28-320 ФИРТ

Проверила: Закиева Е.Ш.

Уфа, 2005

1. Задание на практику

Объектом исследования является следящая система, структурная схема которой представлена на рис. 1.

g(t)

K_ред

s

K_изм

(t)

I_у

u_д

K_у



L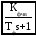

Рис. 1. Структурная схема следящей системы

Здесь: К_изм - передаточный коэффициент измерительного устройства;

К_фчв, Т_ф - коэффициент передачи и постоянная времени фазочувстви-тельного выпрямителя;

К_у коэффициент усиления электронного усилителя;

К_эму, Т_э - коэффициент передачи и постоянная времени электрома-шинного усилителя;

К_д, Т_д - коэффициент передачи и постоянная времени электрического двигателя;

К_ред - коэффициент передачи редуктора.

Кизм В/град	Кэму В /мА	Тфчв сек	Тэму сек	Кд	Тд сек	Кред	Кфчв	Задающие воздействие		Допустимые ошибки
										ск град	уск град
15	2,0	0,004	0,015	2,15	0,3	0,003	1	17	2,8	0,1	-

2. Выполнение

1. Исследовать устойчивость замкнутой системы с помощью критерия Гурвица. Приняв коэффициент усиления электронного усилителя К_у=100.

Передаточная функция разомкнутой системы:

Характеристический полином:

Матрица коэффициентов:

=

Все определители матрицы коэффициентов положительны система устойчива.

Определить критическое значение коэффициента усиления К_у, когда система находится на границе устойчивости.

Характеристический полином:

Матрица коэффициентов:

=

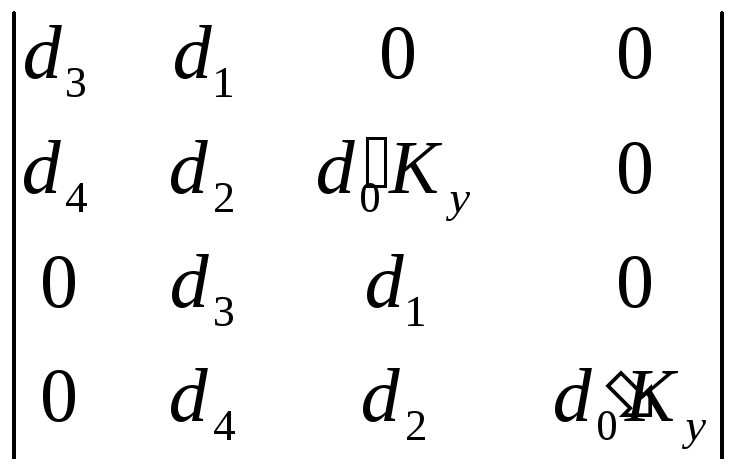входит в определитель . Записываем определитель и приравниваем его к нулю, чтобы найти критическое значение .

– критическое значение , при котором система будет находиться на границе устойчивости.

2. Исследовать устойчивость замкнутой системы с помощью критерия Рауса.

Характеристический полином:

	1	2	3

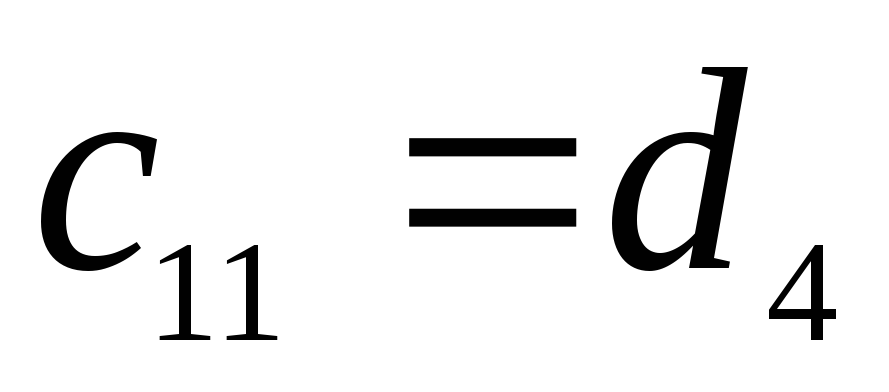
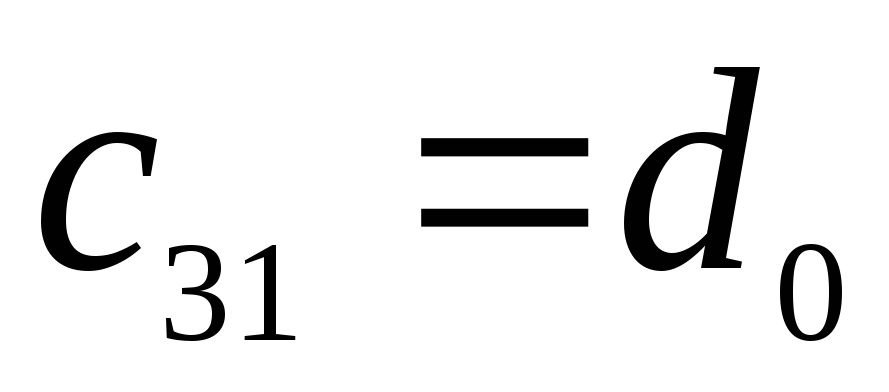
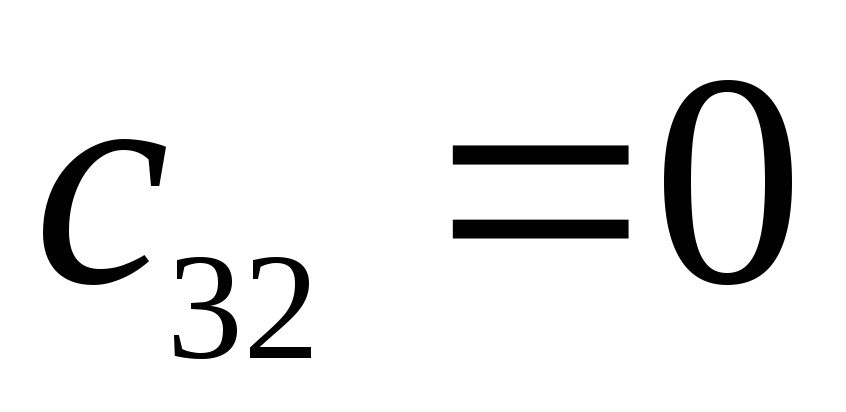
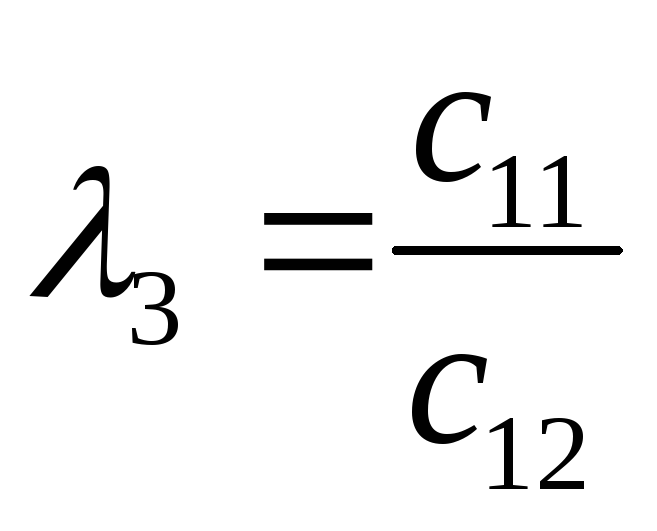
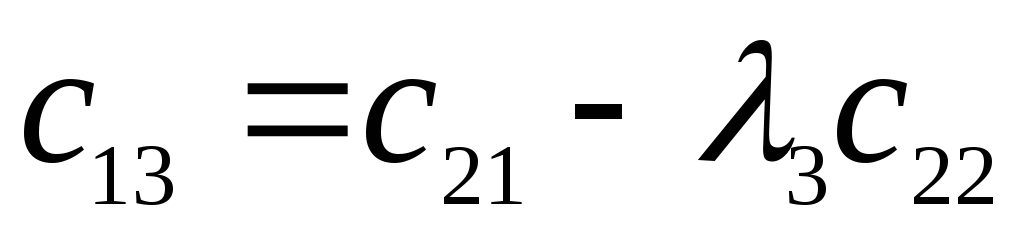
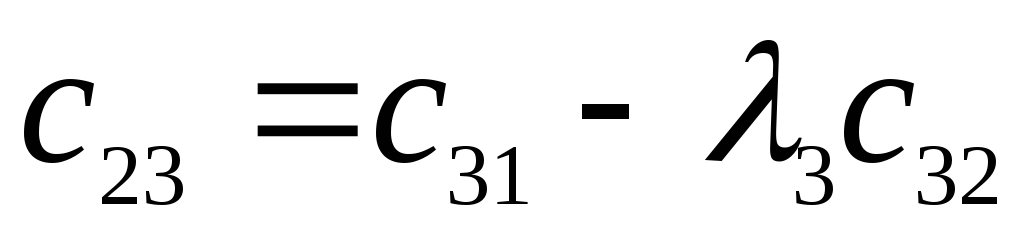
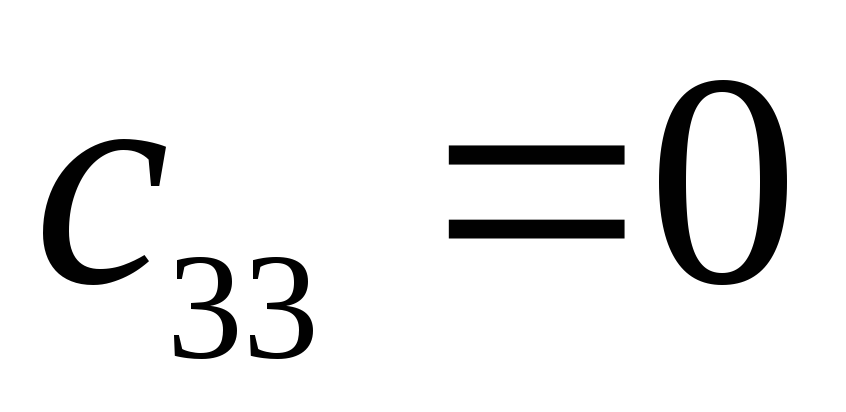
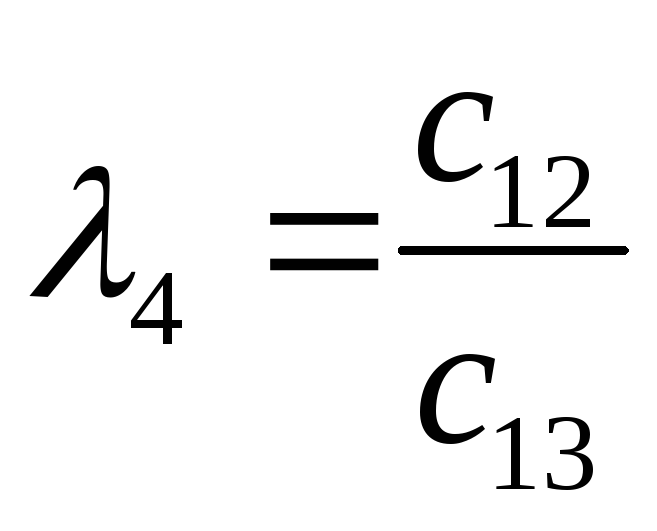
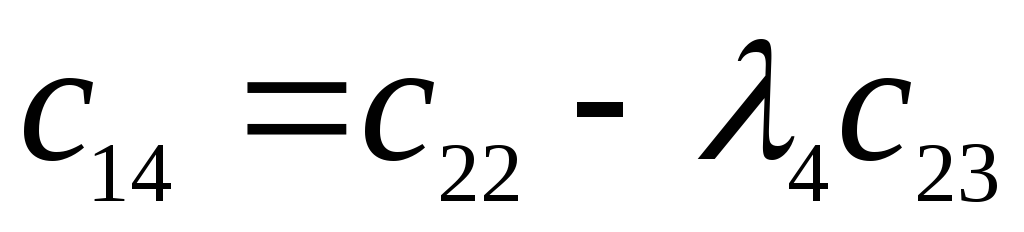
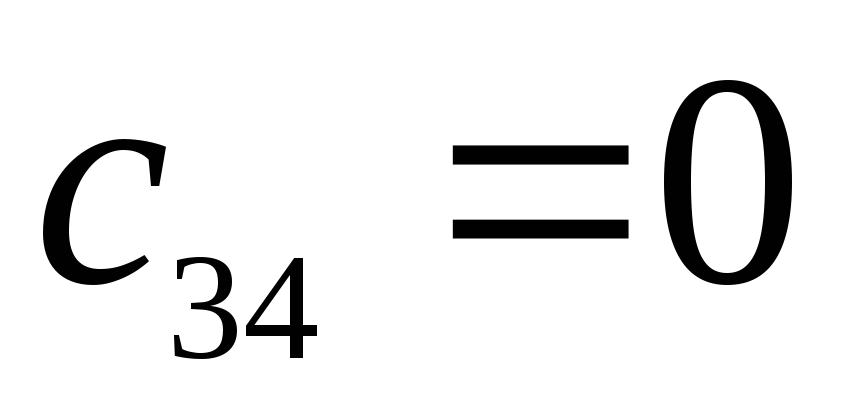
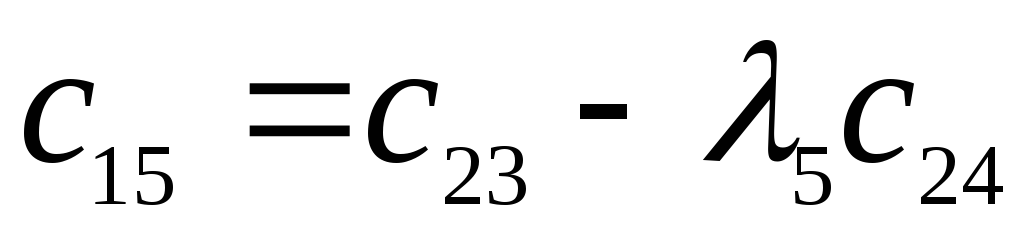
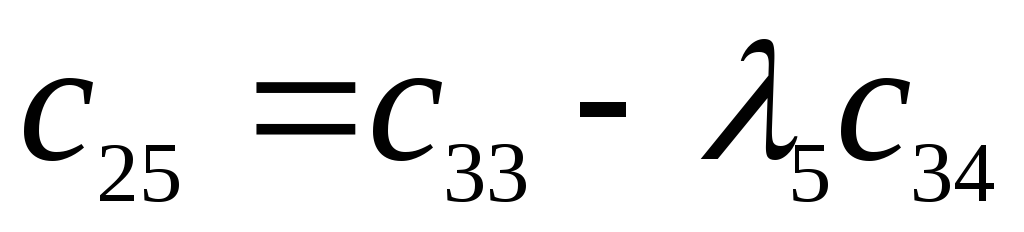
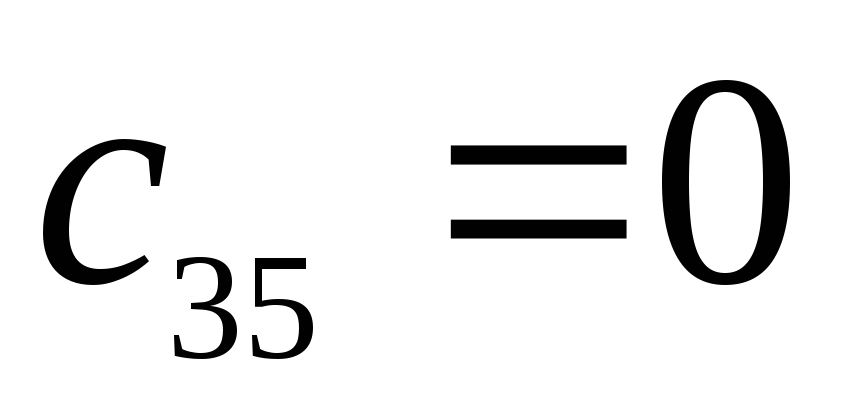
	1	2	3
	0.000018	0.319	19.35
	0.00576	1	0
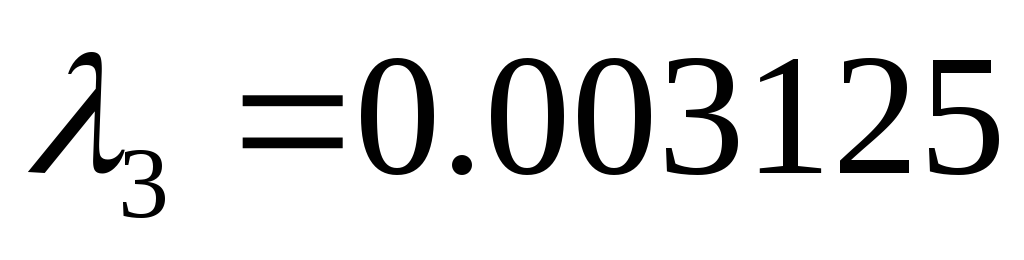
	0.315875	19.35	0
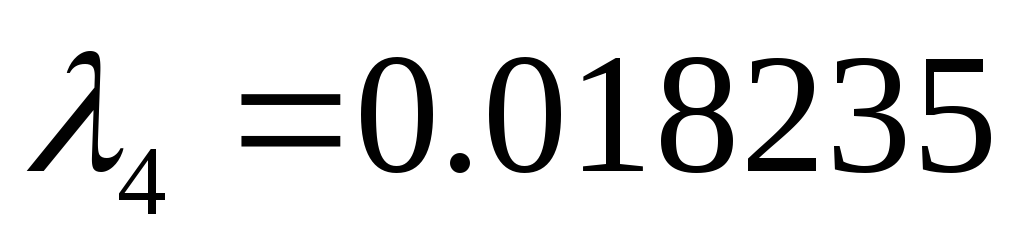
	0.647152	0	0
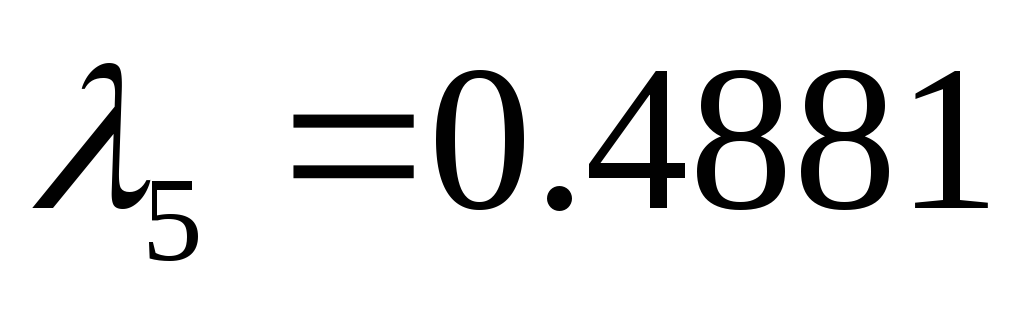
	19.35	0	0

Коэффициенты 1-го столбца таблицы Рауса положительны система устойчива.

3. Исследовать устойчивость замкнутой системы с помощью критерия Михайлова.

Характеристический полином:

Выделяем действительную и мнимую части:

Таблица

	0	7.817	13.176	132.9
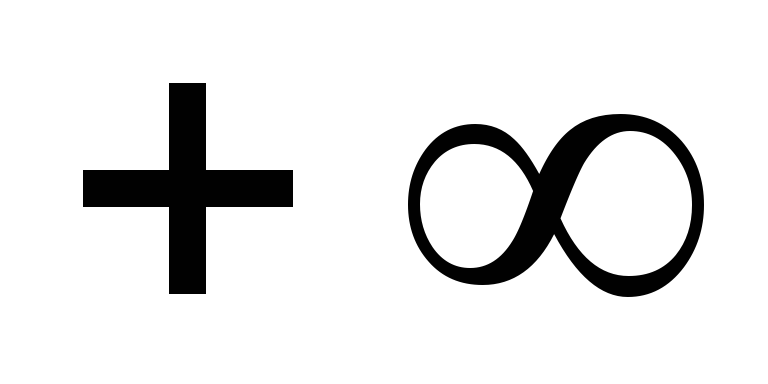
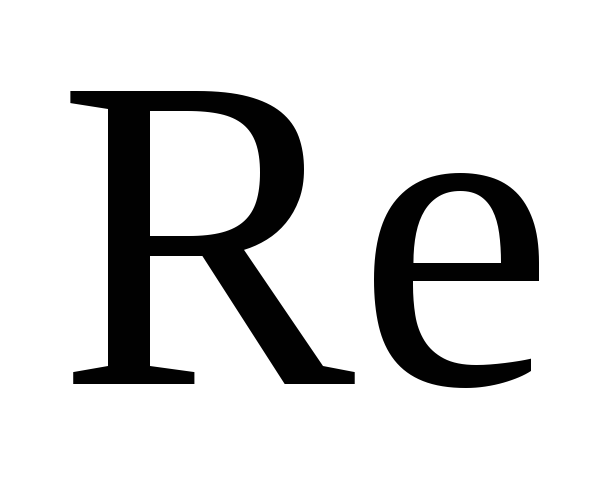
	19.35	0	−35.49	0
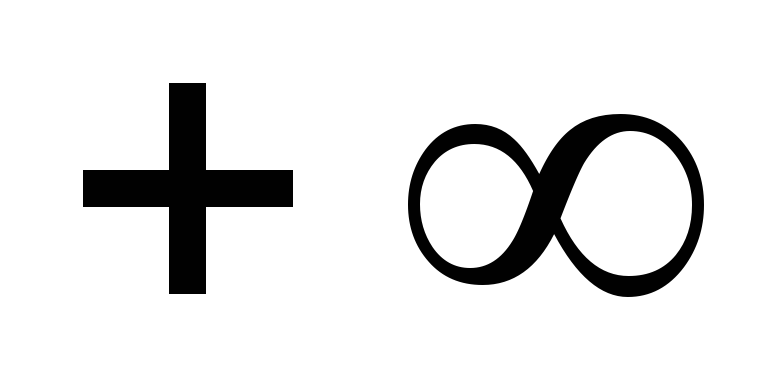
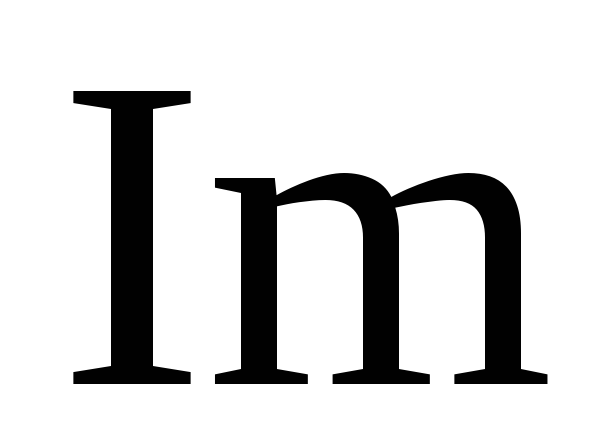
	0	5.0654	0	−13386.75

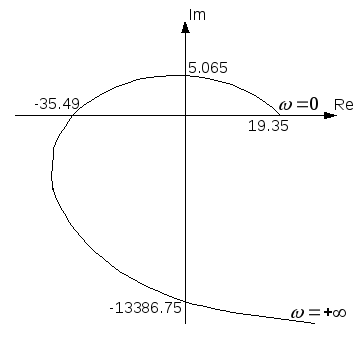
Критерий Михайлова:

САУ устойчива, если годограф начинается на действительной оси и с ростом от 0 до обходит последовательно в положительном направлении, то есть против часовой стрелки квадрантов, где – степень характеристи-ческого уравнения.

Исследуемая система устойчива, т.к. годограф последовательно обходит 4 квадранта.

4. Исследовать устойчивость замкнутой системы с помощью критерия Найквиста.

Передаточная функция разомкнутой системы:

(АФХ)

АЧХ:

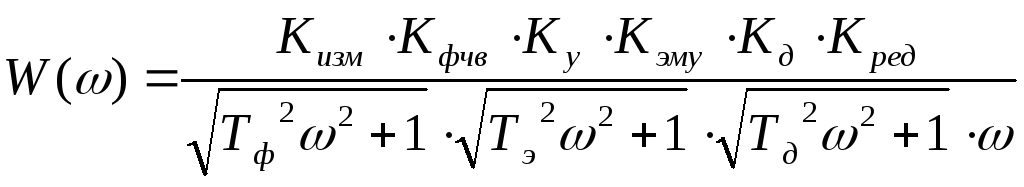
ФЧХ:

0	+∞	-1,5708	−∞	−∞
10	0,806196	-3,00871	-0,79909	-0,10681
20	0,202484	-3,34773	-0,1982	0,041445
30	0,085989	-3,57322	-0,0781	0,035973
40	0,045354	-3,75753	-0,03702	0,026202
50	0,026926	-3,91592	-0,01925	0,018828
60	0,01724	-4,05445	-0,01054	0,013641
70	0,011643	-4,1768	-0,00594	0,010012
80	0,008186	-4,28571	-0,00339	0,007452
90	0,005942	-4,38338	-0,00192	0,005623
100	0,004427	-4,47157	-0,00106	0,004299
110	0,00337	-4,55174	-0,00054	0,003327
120	0,002614	-4,62504	-0,00023	0,002604
130	0,00206	-4,69242	-4,1E-05	0,002059
140	0,001645	-4,75465	6,95E-05	0,001644
150	0,001331	-4,81237	0,000133	0,001324
160	0,001088	-4,86608	0,000167	0,001075
170	0,000898	-4,91623	0,000182	0,00088
180	0,000748	-4,96319	0,000186	0,000725
190	0,000628	-5,00726	0,000182	0,000601
200	0,000531	-5,04871	0,000175	0,000501
210	0,000452	-5,08778	0,000166	0,00042
220	0,000387	-5,12466	0,000155	0,000354
230	0,000333	-5,15953	0,000144	0,0003
240	0,000288	-5,19255	0,000133	0,000256
250	0,000251	-5,22385	0,000123	0,000219
260	0,000219	-5,25357	0,000113	0,000188
270	0,000192	-5,28181	0,000104	0,000162
280	0,000169	-5,30868	9,5E-05	0,00014
290	0,00015	-5,33427	8,71E-05	0,000122
300	0,000133	-5,35867	7,99E-05	0,000106
+∞	0	-2π	0	0

АФХ разомкнутой системы

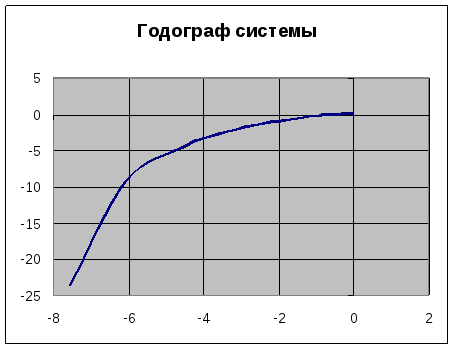
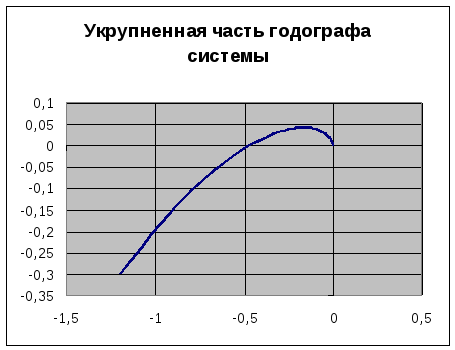
Критерий Найквиста:

САУ, нейтральная в разомкнутом состоянии, устойчива, если годограф разомкнутой системы с его дополнением до бесконечности не охватывает точку .

Исследуемая система устойчива, т.к. годограф не охватывает точку .

5. Исследовать устойчивость замкнутой системы с помощью логарифми-ческих частотных характеристик, оценить запасы устойчивости по фазе и амплитуде.

Запас устойчивости по фазе:

Запас устойчивости по модулю :

6. Построить кривую D-разбиения по параметру К_у.

Характеристический полином:

Выделяем действительную и мнимую части:

Построим вспомогательные графики

и

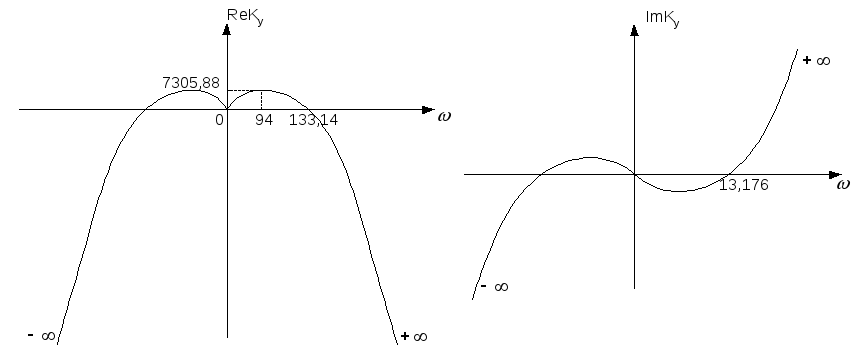
		0	13.176	94	133.14
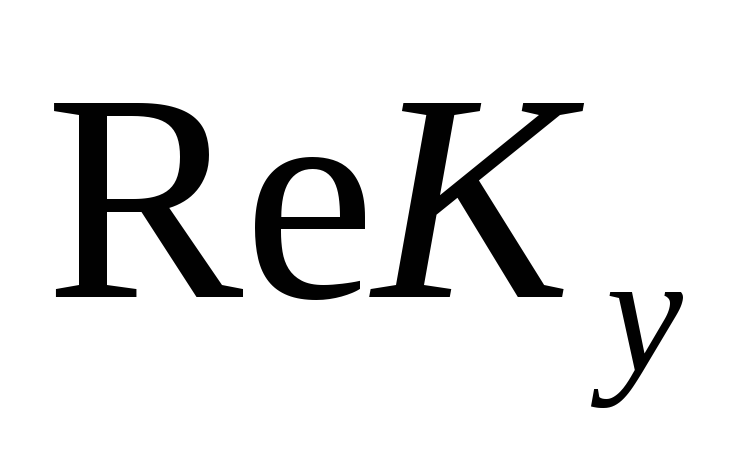
		0	283.4	7305.88	0
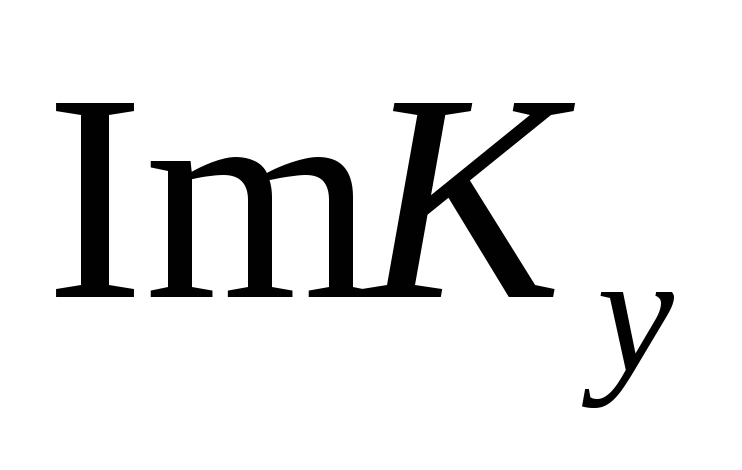
		0	0	24238.21	69565.83

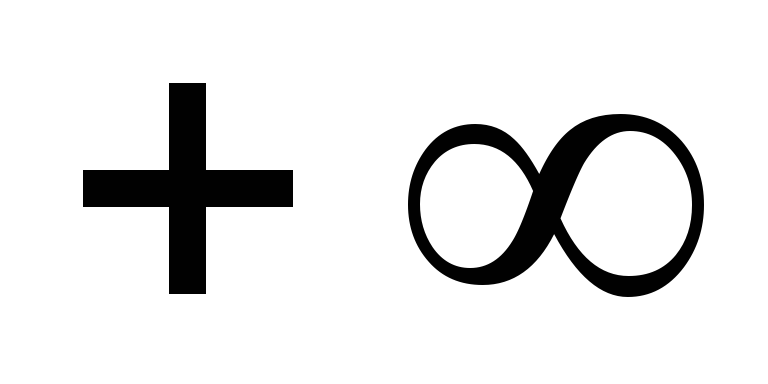
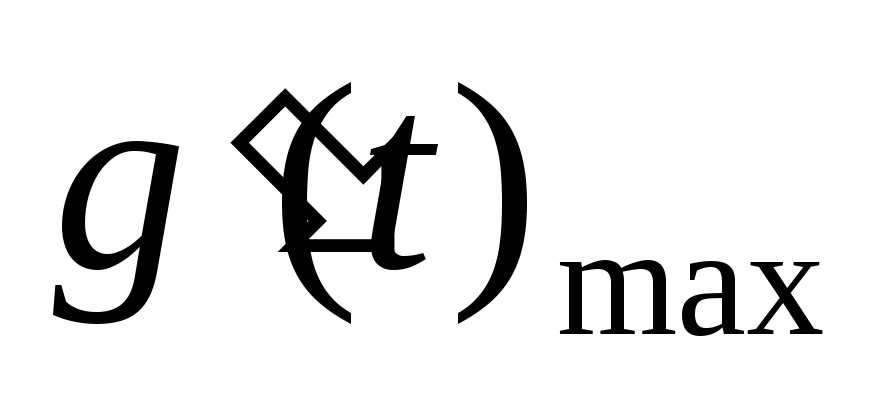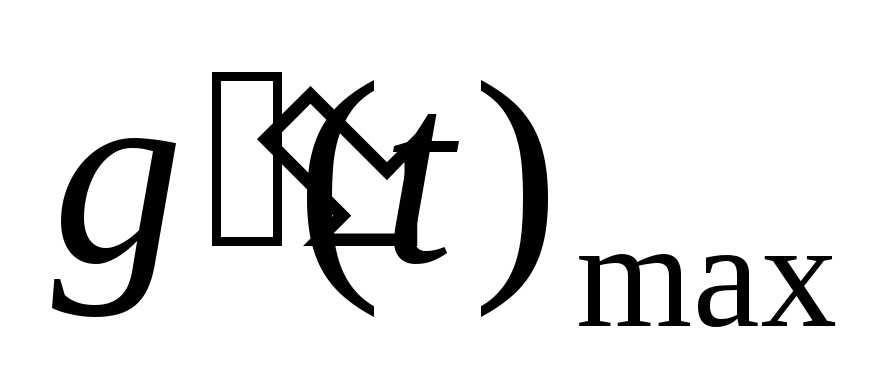7. С помощью метода коэффициента ошибок с учетом задающего воздействия ( и ) и заданных скоростной и ошибки управления по ускорению рассчитать требуемый коэффициент усиления электронного усилителя К_у.

Передаточная функция разомкнутой системы: