
Відстані від основи висоти піраміди
Відстань від
основи висоти піраміди до бічного ребра
— перпендикуляр, опущений із точки О на
це ребро (див. рисунок). Зверніть увагу: ![]() ,
але
,
але ![]() на
рисунку не повинен бути прямим: кути
при паралельному проектуванні не
зберігаються.
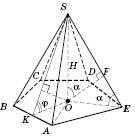
OF —
відстань від основи висоти до бічного
ребра SE;
ON —
відстань від основи висоти до бічної
грані ASB (про
цю відстань докладніше дивись нижче).
на
рисунку не повинен бути прямим: кути
при паралельному проектуванні не
зберігаються.
OF —
відстань від основи висоти до бічного
ребра SE;
ON —
відстань від основи висоти до бічної
грані ASB (про
цю відстань докладніше дивись нижче).
![]() ,
де
,
де ![]() —
кут між ребром SE і
площиною основи.
—
кут між ребром SE і
площиною основи.
Відстань від основи висоти до бічної грані
Нехай ![]() ,
тоді
,
тоді ![]() за
теоремою про три перпендикуляри.
Отже, ABперпендикулярна
до площини SOK.
Звідси, якщо
за
теоремою про три перпендикуляри.
Отже, ABперпендикулярна
до площини SOK.
Звідси, якщо ![]() ,
то ON перпендикулярна
до площини ASB.
,
то ON перпендикулярна
до площини ASB.
![]() .
Піраміда
називається правильною,
якщо її основою є правильний многокутник,
а основа висоти збігається з центром
многокутника. Віссю правильної
піраміди називається пряма, яка містить
її висоту. Бічні ребра правильної
піраміди рівні, бічні грані — рівні
рівнобедрені трикутники. Висота бічної
грані, проведена з вершини піраміди,
називається апофемою.
Вона є бісектрисою та медіаною бічної
грані, оскільки та є рівнобедреним
трикутником.
Теорема. Бічна поверхня
правильної піраміди дорівнює добутку
півпериметра основи на апофему.
.
Піраміда
називається правильною,
якщо її основою є правильний многокутник,
а основа висоти збігається з центром
многокутника. Віссю правильної
піраміди називається пряма, яка містить
її висоту. Бічні ребра правильної
піраміди рівні, бічні грані — рівні
рівнобедрені трикутники. Висота бічної
грані, проведена з вершини піраміди,
називається апофемою.
Вона є бісектрисою та медіаною бічної
грані, оскільки та є рівнобедреним
трикутником.
Теорема. Бічна поверхня
правильної піраміди дорівнює добутку
півпериметра основи на апофему.
![]() ;
; ![]() ,
де Р —
периметр основи, а —
сторона основи, l —
довжина апофеми.
Правильна трикутна
піраміда
В основі правильної трикутної
піраміди лежить рівносторонній трикутник,
який зображується довільним трикутником
(див. рисунок).
,
де Р —
периметр основи, а —
сторона основи, l —
довжина апофеми.
Правильна трикутна
піраміда
В основі правильної трикутної
піраміди лежить рівносторонній трикутник,
який зображується довільним трикутником
(див. рисунок).
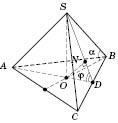 Центром
Центром ![]() є
точка перетину його бісектрис, котрі
водночас є висотами і медіанами. Медіани
при паралельному проектуванні зображуються
медіанами. Тому будуємо дві медіани
основи. Точка їх перетину — основа
висоти піраміди. Зображуємо висоту, а
потім з’єднуємо вершину піраміди з
вершинами основи. Отримаємо бічні
ребра.
На рисунку:
є
точка перетину його бісектрис, котрі
водночас є висотами і медіанами. Медіани
при паралельному проектуванні зображуються
медіанами. Тому будуємо дві медіани
основи. Точка їх перетину — основа
висоти піраміди. Зображуємо висоту, а
потім з’єднуємо вершину піраміди з
вершинами основи. Отримаємо бічні
ребра.
На рисунку: ![]() —
кут нахилу бічного ребра до площини
основи (однаковий для всіх ребер);
—
кут нахилу бічного ребра до площини
основи (однаковий для всіх ребер); ![]() —
кут нахилу бічної грані до площини
основи (однаковий для всіх
граней).
Нехай
—
кут нахилу бічної грані до площини
основи (однаковий для всіх
граней).
Нехай ![]() .
Тоді
.
Тоді ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() .
Отже,
.
Отже, ![]() .
.
![]() ;
; ![]() .
Площина
осьового перерізу ASD є
площиною симетрії правильної трикутної
піраміди.
Ця площина перпендикулярна
до площини основи і площини грані BSC.
Цікаво
також відмітити, що мимобіжні ребра
піраміди (SA і BC, SB і AC, SC і AB)
є перпендикулярними. Якщо
.
Площина
осьового перерізу ASD є
площиною симетрії правильної трикутної
піраміди.
Ця площина перпендикулярна
до площини основи і площини грані BSC.
Цікаво
також відмітити, що мимобіжні ребра
піраміди (SA і BC, SB і AC, SC і AB)
є перпендикулярними. Якщо ![]() ,
то ON є
відстанню від основи висоти не тільки
до анафеми, а й до бічної грані BSC.
,
то ON є
відстанню від основи висоти не тільки
до анафеми, а й до бічної грані BSC.
![]() .
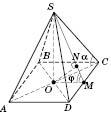
Правильна
чотирикутна піраміда
В основі правильної
чотирикутної піраміди лежить квадрат,
який зображується довільним паралелограмом.
Його центром є точка перетину діагоналей.
Ця точка — основа висоти піраміди.
Нехай
сторона квадрата а (див.
рисунок).
Тоді
.
Правильна
чотирикутна піраміда
В основі правильної
чотирикутної піраміди лежить квадрат,
який зображується довільним паралелограмом.
Його центром є точка перетину діагоналей.
Ця точка — основа висоти піраміди.
Нехай
сторона квадрата а (див.
рисунок).
Тоді
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
 Зверніть
увагу:
Зверніть
увагу: ![]() ,
, ![]() ,
тобто
,
тобто ![]() .
При
паралельному проектуванні паралельність
зберігається.
.
При
паралельному проектуванні паралельність
зберігається.
![]() ;
; ![]() .
Відстань
від основи висоти до бічної
грані:
.
Відстань
від основи висоти до бічної
грані:
![]() ;
; ![]() .
Правильна
шестикутна піраміда
В основі правильної
шестикутної піраміди лежить правильний
шестикутник (див. рисунок). Його центром
є точка перетину діагоналей. Ця точка
— основа висоти піраміди.
.
Правильна
шестикутна піраміда
В основі правильної
шестикутної піраміди лежить правильний
шестикутник (див. рисунок). Його центром
є точка перетину діагоналей. Ця точка
— основа висоти піраміди.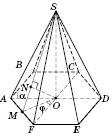 Тоді
Тоді ![]() ;
Нехай
сторона правильного
шестикутника а.
;
Нехай
сторона правильного
шестикутника а.
![]() ;
;
![]() ;
;
![]()
![]() .
.
![]() ;
; ![]() .
Зрізана
піраміда
Зрізаною
пірамідою називається
многогранник, який залишиться, якщо від
піраміди відділити площиною, яка
паралельна основі, піраміду з тією ж
вершиною.
Теорема. Площина, яка
паралельна основі піраміди й перетинає
її, відтинає подібну піраміду.
Зверніть
увагу: щоб правильно зобразити зрізану
піраміду, треба починати із зображення
вихідної повної піраміди (див.
рисунок).
.
Зрізана
піраміда
Зрізаною
пірамідою називається
многогранник, який залишиться, якщо від
піраміди відділити площиною, яка
паралельна основі, піраміду з тією ж
вершиною.
Теорема. Площина, яка
паралельна основі піраміди й перетинає
її, відтинає подібну піраміду.
Зверніть
увагу: щоб правильно зобразити зрізану
піраміду, треба починати із зображення
вихідної повної піраміди (див.
рисунок).
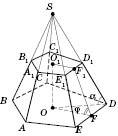 Основи
зрізаної піраміди — подібні многокутники.
Бічні грані — трапеції.
Основи
зрізаної піраміди — подібні многокутники.
Бічні грані — трапеції. ![]() —
висота зрізаної піраміди,
—
висота зрізаної піраміди, ![]() —
висота бічної грані,
—
висота бічної грані, ![]() —
кут нахилу бічного ребра до площини
основи (будь-якої),
—
кут нахилу бічного ребра до площини
основи (будь-якої), ![]() —
кут нахилу бічної грані до площини
нижньої основи.
Правильна
зрізана піраміда —
це зрізана піраміда, яку дістали з
правильної піраміди.
Її бічні ребра
рівні й нахилені до площини основи під
одним і тим самим кутом. Її бічні грані
дорівнюють рівнобічній трапеції і
нахилені до площини нижньої основи під
одним і тим самим кутом. Висоти бічних
граней піраміди називаються апофемами.
Бічна
поверхня правильної зрізаної піраміди
дорівнює добутку півсуми периметрів
основ і апофеми.
—
кут нахилу бічної грані до площини
нижньої основи.
Правильна
зрізана піраміда —
це зрізана піраміда, яку дістали з
правильної піраміди.
Її бічні ребра
рівні й нахилені до площини основи під
одним і тим самим кутом. Її бічні грані
дорівнюють рівнобічній трапеції і
нахилені до площини нижньої основи під
одним і тим самим кутом. Висоти бічних
граней піраміди називаються апофемами.
Бічна
поверхня правильної зрізаної піраміди
дорівнює добутку півсуми периметрів
основ і апофеми.
![]() ,
де Pн
і Pв
— периметри відповідних основ, l —
апофема.
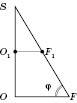
На рисунках зображені фігури,
які буває дуже корисним розглянути при
розв’язуванні задач на зрізану
піраміду.
,
де Pн
і Pв
— периметри відповідних основ, l —
апофема.
На рисунках зображені фігури,
які буває дуже корисним розглянути при
розв’язуванні задач на зрізану
піраміду.
![]() ;
;
![]() .
. 
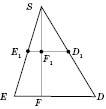
![]() ;
;

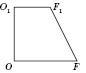
![]() —
прямокутна трапеція.
—
прямокутна трапеція.
![]() —
висота зрізаної піраміди.
—
висота зрізаної піраміди.
![]() — висота
бічної грані.
У випадку, коли зрізана
піраміда правильна, відрізки OD і
— висота
бічної грані.
У випадку, коли зрізана
піраміда правильна, відрізки OD і ![]() є
радіусами описаного кола, а OF і
є
радіусами описаного кола, а OF і ![]() —
радіусами вписаного кола для нижньої
і верхньої основи відповідно.
—
радіусами вписаного кола для нижньої
і верхньої основи відповідно.
