лабораторная работа / lab5

Министерство общего образования Российской Федерации

Саратовский государственный технический университет

Балаковский Институт Техники Технологии и Управления

Факультет: ИСФ

Кафедра: УИТ

Специальность: УИТ

Лабораторная работа №5

По ТАУ

Метод гармонической линеаризации

Выполнил ст. гр. УИТ – 42

Поляков А.В.

Принял: Мефедова Ю.А.

Балаково – 2004

1 Исследуемая нелинейная система имеет вид:

x(t) ε(t) g(t) y(t)

Нелинейный элемент представляет собой чувствительный элемент с релейной характеристикой, для которого коэффициенты гармонической линеаризации:

,

.

2.1 Передаточная функция исполнительного устройства имеет вид:

.

Передаточная функция объекта регулирования:

.

Передаточная функция линейной части системы:

,

где .

На основании , запишем характеристическое уравнение замкнутой системы:

, следовательно

,

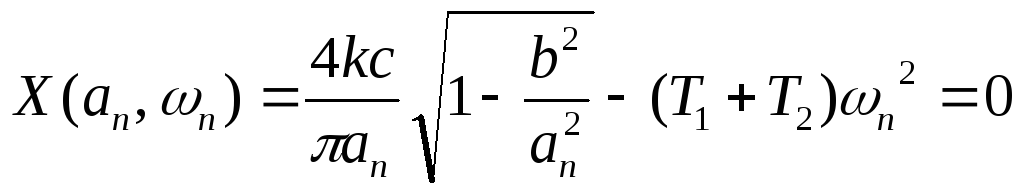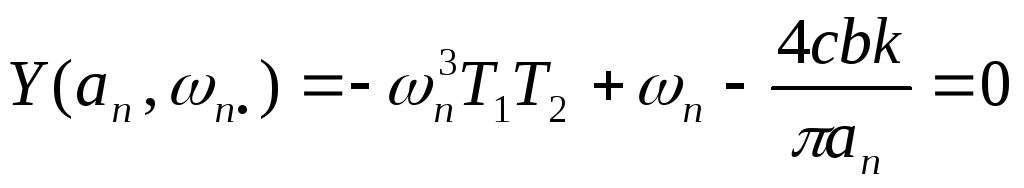. Дано: k=12 (1/сек), T₁=0,3 сек, T₂ = 0,5 сек, с = 1,5; b=0,2.

Тогда параметры периодического движения равны:

a1_n = -3, a2_n = 7, a3_n = -0.2.

w1_n = 3, w2_n = 2, w3_n = 0 1(/сек).

2.2 Определим параметры автоколебаний в линеаризованной САУ с помощью критерия Михайлова. При возникновении автоколебаний система будет находиться на границе устойчивости и годограф Михайлова в этом случае будет проходить через начало координат.

Найдем параметры автоколебаний при том условии, что нелинейный элемент в системе представляет собой чувствительный элемент, имеющий релейную характеристику с гистерезисом, для которого коэффициенты гармонической линеаризации:

,

.

Линейная часть осталась неизменной.

Запишем характеристическое уравнение замкнутой системы

.

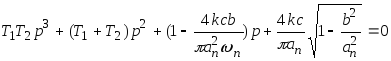Получим годограф Михайлова заменой .

.

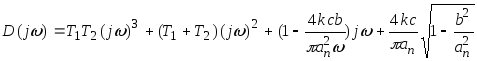Необходимо подобрать такую амплитуду колебаний , при которой годограф пройдет через начало координат. Необходимо отметить, что при этом текущая частота , так как именно в этом случае кривая пройдет через начало координат.

Годограф Михайлова проходит через начало координат. Кривая проходит через начало координат уже при a_n = 9 в. При дальнейшем бесконечном увеличении а_n годограф будет всегда проходить через начало координат

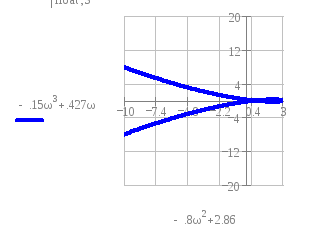
_{2.3Частоту колебаний при этом можно найти из условия равенства нулю модуля .}

Частоты колебаний (3.4; 1.9; 2.95*10^-3).

Полученное периодическое решение, определяемое значением амплитуды и частоты , необходимо исследовать на устойчивость. Если решение устойчиво, то в системе имеет место автоколебательный процесс (устойчивый предельный цикл). В противном случае предельный цикл будет неустойчивым.

При исследовании устойчивости периодического решения по критерию Михайлова установлено, что при годограф проходит через начало координат. Если дать малое приращение , то кривая займет положение либо выше нуля, либо ниже. Так в последнем примере дадим приращение в, то есть

a_n = 10 и a_n = 8.

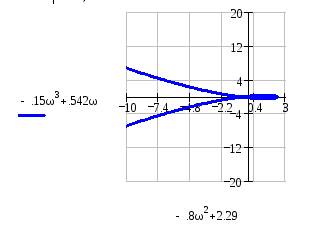
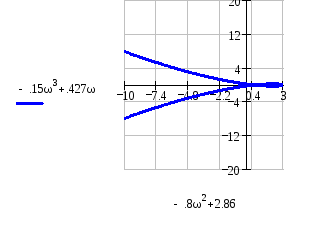
При кривая проходит левее начала координат, что говорит об устойчивости системы и затухающем переходном процессе. При годограф проходит правее, система является неустойчивой и переходный процесс является расходящимся. Следовательно периодическое решение с амплитудой a_n = 9 в и частотами колебаний (3.4; 1.9; 2.95*10^-3) устойчиво.

Используем критерий для исследования устойчивости периодического решения, полученного в примере 1.

Так как

,

,

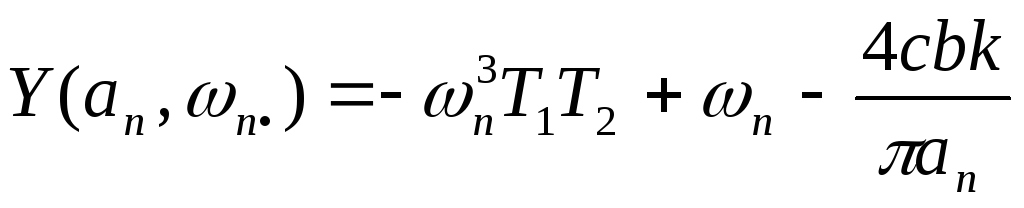Следовательно: >0

Периодическое решение, полученное в примере 1 устойчиво.

Теперь рассмотрим частотный способ определения параметров автоколебаний. Запишем частотную передаточную функцию разомкнутой системы

.

По критерию Найквиста в замкнутой системе возникнут колебания, если амплитудно-фазовая частотная характеристика разомкнутой системы пройдет через точку (-1, j0). Эти колебания будут устойчивыми, если при возрастании амплитуды на АФЧХ не будет охватывать точку (-1, j0), при этом колебания затухают и при АФЧХ будет охватывать точку (-1, j0), при этом колебания расходятся.

Параметры автоколебаний определим частотным способом. Запишем частотную передаточную функцию разомкнутой системы

.

АФЧХ разомкнутой системы проходит через точку с координатами

(-1, j0) при амплитуде a_n = 6 в.

_{Частота колебаний:}

_{, .}

=> _n=2.8. Результаты расчетов, выполненные двумя разными способами, практически совпадают. Давая различные по знаку приращения нетрудно показать, что полученные колебания устойчивые.

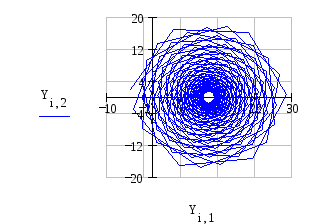
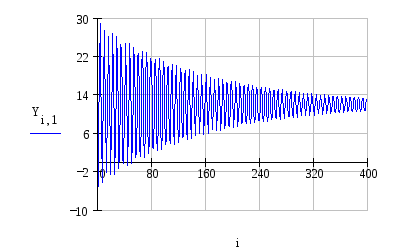
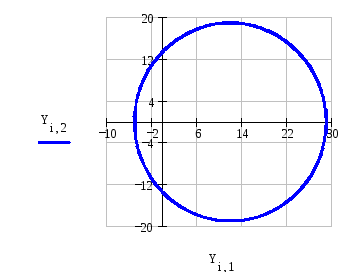
3 Построим фазовый портрет и исследуем на устойчивость систему:

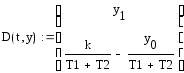
олучили предельный цикл, значит система находится на границе устойчивости, что показывает и переходный процесс.

Изменив условии в решении дифференциального уравнения, т.е. интервал от х1 до х2, получим, что система оказалась неустойчивой: