лабораторная работа / Практическая работа 1 - 9

Дано:

структурная схема системы управления (СУ)

Провести анализ устойчивости СУ методами:

1. Ляпунова

2. Рауса

3. Гурвица

4. Льенера-Шипара

5. Михайлова

6. Найквиста

7. D-разбиения

8. Шур-Кона

Передаточная функция разомкнутой системы:

Передаточная функция замкнутой системы:

Система является устойчивой по критерию Ляпунова, если все корни характеристического уравнения лежат в левой полуплоскости.

Характеристическое уравнение замкнутой системы:

Уравнение имеет 6 корней, лежащих в левой полуплоскости, следовательно разомкнутая система устойчива.

Определим устойчивость системы по методу Рауса.

Составим программу для построения таблицы Рауса:

Коэффициенты характеристического уравнения:

Поскольку все коэффициенты 1 столбца таблицы положительны, система устойчива.

Определим устойчивость системы по методу Гурвица.

Составим программу для построения определителей Гурвица:

Вычислим определители:

Все определители Гурвица положительны, следовательно система устойчива.

Критерий Льенера-Шипара состоит в следующем: если выполняется необходимое условие устойчивости (все коэффициенты характеристического уравнения положительны), достаточно вычислить только четные (нечетные) определители Гурвица; если все они положительны, система устойчива.

Нечетные определители Гурвица больше 0, система устойчива.

Определим устойчивость СУ по критерию Михайлова.

Заменим в характеристическом уравнении p на j и выделим действительную и мнимую части:

Построим годограф Михайлова:

Система устойчива по критерию Михайлова, если годограф Михайлова, начинаясь на положительной вещественной полуоси, при изменении частоты от нуля до бесконечности повернулась в положительном направлении вокруг начала координат последовательно, нигде не обращаясь в ноль на n квадрантов, где n - порядок характеристического уравнения.

Как видно из графика, кривая Михайлова началась на вещественной положительной полуоси и прошла 6 квадрантов в положительном направлении, нигде не обращаясь в 0, следовательно система устойчива.

Определим устойчивость замкнутой САУ по АФЧХ разомкнутой методом Найквиста.

Найдем АФЧХ разомкнутой системы:

Построим годограф Найквиста (АФЧХ разомкнутой системы):

Чтобы САУ, устойчивая в разомкнутом состоянии, была устойчива в замкнутом, необходимо и достаточно, чтобы кривая АФЧХ разомкнутой системы при изменении частоты от нуля до бесконечности не охватывала точку (-1 + j0).

Так как разомкнутая система астатическая 1 порядка, дополним график дугой бесконечного радиуса, поворачивающейся при =0 на угол от 0 до (/2)*, где =1 - порядок астатичности.

Как видно из графика, годограф Найквиста не охватывает точку (-1 + j0), следовательно система будет устойчива в замкнутом состоянии.

Определим область устойчивости системы методом D-разбиения.

D-разбиение - разбиение плоскости искомого параметра на области, в которых число корней с положительной действительной частью постоянно. Область устойчивости - область с числом корней с положительной вещественной частью, равным 0. Оптимальное значение параметра выбирается на вещественной оси в середине области устойчивости. Граница D-разбиения - решение характеристического уравнения D(j) = 0 для искомого параметра при  = - ... +.

Построим D-разбиение по параметру T₄.

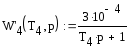
Передаточная функция замкнутой системы:

Характеристическое уравнение:

Решим его относительно искомого параметра:

Заменим p на j:

По правилу штриховки штрихуется левая (в направлении возрастания частоты) часть прямой.

При переходе через границу D-разбиения в сторону штриховки, число корней с положительной вещественной частью уменьшается на 1. Значение параметра выбирают на положительной вещественной полуоси в середине области устойчивости. В нашем случае область устойчивости от 0 до бесконечности, поэтому значение параметра может быть любым.

Определим устойчивость дискретной СУ методом Шур-Кона.

Для этого произведем z-преобразование передаточной функции системы.

Зададим период дискретизации:

Домножим на фиксатор нулевого порядка:

Заменим комплексную переменную z на псевдочастоту.

Составим характеристическое уравнение относительно :

Составим определители по Шур-Кону из коэффициентов уравнения.

Составим программу для построения определителей Шур-Кона:

Составим вектор коэффициентов характеристического уравнения:

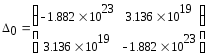
Вычислим определители:

Так как знаки определителей на четных и нечетных местах не чередуются, дискретная система неустойчива.