
- •1. Последовательности. Определение,
- •2.Предел последовательности. Сходимость.
- •3.Свойства сходящихся последовательностей.
- •4. Бесконечно малые функции и их свойства.
- •5. Определение функции. Способы задания функции.
- •6.Классификация основных элементарных функций.
- •7. Предел функции. Теоремы о пределах.
- •8. Односторонние пределы. Несобственные пределы.
- •9.Непрерывность функции в точке и в интервале. Свойства непрерывных функций.
- •10. Эквивалентные бесконечно малые функции и их использование при вычислении пределов. Замечательные пределы. (на примере)
- •11. Разрывы функций. Классификация разрывов.
- •12. Производная функции. Геометрический смысл производной.
- •13. Теоремы о производной суммы, произведения и частного.
- •14. Производная сложной и обратной функции (таблица). Понятие о логарифмической производной(порядок логарифмического дифференцирования. Показать на примере)
- •15. Дифференциал, связь дифференциала и приращения функции.
- •21. Экстремум функции, точки перегиба, асимптоты.
- •22. Правила исследования функций.
- •28. Разложение рациональной функции на простейшие дроби.
- •29. Интегрирование рациональных функций.
15. Дифференциал, связь дифференциала и приращения функции.
Определение. Дифференциалом функции
называется главная, линейная относительно
![]() часть приращения функции, равная
произведению производной на приращение
независимой переменной
часть приращения функции, равная
произведению производной на приращение
независимой переменной
![]() .
.
Геометрический
смысл дифференциала. Дифференциал
функции есть приращение ординаты
касательной, проведенной к графику
функции
![]() в данной точке, когда
в данной точке, когда
![]() получает приращение
получает приращение
![]() .
.
Свойства дифференциала:
-
 .
. -
 .
. -
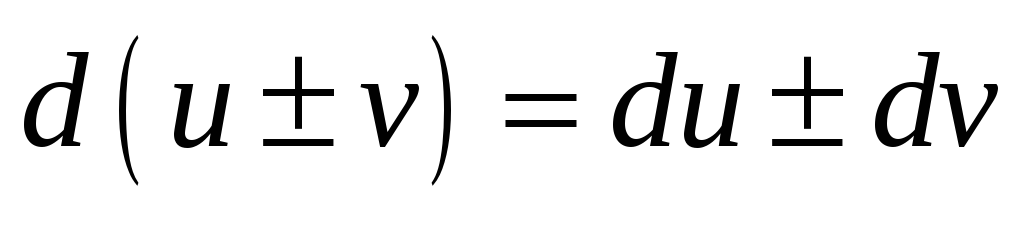 .
. -
 .
. -
 .
.
16. Производные и дифференциалы высших порядков.
Производной
![]() порядка называется производная от
производной
порядка называется производная от
производной
![]() порядка.
порядка.
Дифференциал второго порядка (или вторым
дифференциалом)
![]() функции
функции
![]() называется дифференциал от дифференциала
первого порядка этой функции, т.е.
называется дифференциал от дифференциала
первого порядка этой функции, т.е.
![]() .
.
Дифференциалом
![]() порядка (или
порядка (или
![]() дифференциалом)
дифференциалом)
![]() функции
функции
![]() называется дифференциал от дифференциала
называется дифференциал от дифференциала
![]() порядка этой функции этой функции,
т.е.
порядка этой функции этой функции,
т.е.![]() .
.
17. Производные основных элементарных функций.
Пусть
![]() .
Воспользуемся схемой нахождения
производной.
.
Воспользуемся схемой нахождения
производной.
Итак, производная
степенной функции равна
![]() .
.
Пусть
![]() .
Воспользуемся схемой нахождения
производной.
.
Воспользуемся схемой нахождения
производной.
Итак, производная
логарифмической функции равна
![]() .
Если
.
Если
![]() ,
то
,
то
![]() .
.
Пусть
![]() .
Воспользуемся схемой нахождения
производной.
.
Воспользуемся схемой нахождения
производной.
Итак, производная
функции
![]() равна
равна
![]() .
.
Пусть
![]() .
.
![]() .
.
18. Теорема Роля. Теорема Лагранжа.
Теорема Роля. Если функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() ,
дифференцируема в интервале
,
дифференцируема в интервале
![]() и принимает равные значения на его
концах, т.е.
и принимает равные значения на его
концах, т.е.
![]() ,
то в интервале
,
то в интервале
![]() найдется по крайне мере одна точка
найдется по крайне мере одна точка
![]() такая, что
такая, что
![]() .
.
Теорема Лагранжа. Если функция
![]() непрерывна на отрезке
непрерывна на отрезке
![]() и дифференцируема в интервале
и дифференцируема в интервале
![]() ,
то в этом интервале найдется по крайне
мере одна точка
,
то в этом интервале найдется по крайне
мере одна точка
![]() такая, что
такая, что
![]() .
.
19. Теорема Коши. Формула Тейлора и Маклорена.
Теорема Коши. Если функции
![]() и
и
![]() непрерывны на отрезке
непрерывны на отрезке
![]() и дифференцируемы в интервале
и дифференцируемы в интервале
![]() ,
причем
,
причем
![]() ,
то в этом интервале найдется по крайне
мере одна точка
,
то в этом интервале найдется по крайне
мере одна точка
![]() такая, что
такая, что
![]() .
.
.
20. Раскрытие неопределенности по правилу Лопиталя.
Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.
Итак, если имеется
неопределенность вида
![]() или
или
![]() ,
то
,
то
![]() .Доказательство.
.Доказательство.
![]() и
и
![]() ,
а также их производные непрерывны в
точке
,
а также их производные непрерывны в
точке
![]() ,
причем
,
причем
![]() и
и
![]() .
В этом случае
.
В этом случае
![]() .Применяя
теорему Лагранжа для функций
.Применяя
теорему Лагранжа для функций
![]() и
и
![]() на отрезке
на отрезке
![]() ,
получим
,
получим
![]() ,
где
,
где![]() ,
,
![]() .При
.При
![]() в силу непрерывности производных
в силу непрерывности производных
![]() и
и
![]() имеем
имеем
![]() и
и
![]() .
Используя теорему о пределе частного
получаем равенство
.
Используя теорему о пределе частного
получаем равенство
![]() .
.
21. Экстремум функции, точки перегиба, асимптоты.
Определение. Точка
![]() называется точкой максимума функции
называется точкой максимума функции
![]() ,
если в некоторой окрестности точки
,
если в некоторой окрестности точки
![]() выполняется неравенство
выполняется неравенство
![]() .
.
Определение. Точка
![]() называется точкой минимума функции
называется точкой минимума функции
![]() ,
если в некоторой окрестности точки
,
если в некоторой окрестности точки
![]() выполняется неравенство
выполняется неравенство
![]() .
.
Теорема. Для того чтобы функция
![]() имела экстремум в точке
имела экстремум в точке
![]() ,
необходимо и достаточно, чтобы ее
производная в этой точке равнялась нулю
или не существовала.
,
необходимо и достаточно, чтобы ее
производная в этой точке равнялась нулю
или не существовала.
Теорема. Если при переходе через
точку
![]() производная дифференцируемой функции
производная дифференцируемой функции
![]() меняет свой знак с плюса на минус, то
точка
меняет свой знак с плюса на минус, то
точка
![]() есть точка максимума функции
есть точка максимума функции
![]() ,
а если с минуса на плюс, - то точка
минимума.
,
а если с минуса на плюс, - то точка
минимума.
Теорема. Если первая производная
![]() дважды дифференцируемой функции равна
нулю в некоторой точке
дважды дифференцируемой функции равна
нулю в некоторой точке
![]() ,
а вторая производная в этой точке
,
а вторая производная в этой точке
![]() положительна, то
положительна, то
![]() есть точка минимума функции
есть точка минимума функции
![]() ;
если
;
если
![]() отрицательна, то
отрицательна, то
![]() - точка максимума.
- точка максимума.
Определение. Функция
![]() называется выпуклой вниз на промежутке
Х, если для любых двух значений
называется выпуклой вниз на промежутке
Х, если для любых двух значений
![]() ,
,
![]() из этого промежутка выполняется
неравенство
из этого промежутка выполняется
неравенство
![]() .
.
Определение. Функция
![]() называется выпуклой вверх на промежутке
Х, если для любых двух значений
называется выпуклой вверх на промежутке
Х, если для любых двух значений
![]() ,
,
![]() из этого промежутка выполняется
неравенство
из этого промежутка выполняется
неравенство
![]() .
.
Определение. Точкой перегиба графика непрерывной функции называется точка, разделяющая интервал, в которых функция выпукла вниз и вверх.
Теорема. Вторая производная
![]() дважды дифференцируемой в точке перегиба
дважды дифференцируемой в точке перегиба
![]() равна нулю, т.е.
равна нулю, т.е.
![]() .
.
Теорема. Если вторая производная
![]() дважды дифференцируемой функции при
переходе через некоторую точку
дважды дифференцируемой функции при
переходе через некоторую точку
![]() меняет свой знак, то
меняет свой знак, то
![]() есть точка перегиба ее графика.
есть точка перегиба ее графика.
Прямая линия
называется асимптотой графика функции
![]() ,
если расстояние от точки
,
если расстояние от точки
![]() ,
лежащей на графике, до этой прямой
стремится к нулю при движении точки по
графику в бесконечность.
,
лежащей на графике, до этой прямой
стремится к нулю при движении точки по
графику в бесконечность.
рямая
![]() называется вертикальной асимптотой
графика функции
называется вертикальной асимптотой
графика функции
![]() ,
если хотя бы одно из предельных значений
,
если хотя бы одно из предельных значений
![]() или
или
![]() равно
равно
![]() или
или
![]() .
.
Прямая
![]() называется горизонтальной асимптотой
графика функции
называется горизонтальной асимптотой
графика функции
![]() при
при
![]()
![]() ,
если
,
если
![]() .Прямая
.Прямая
![]()
![]() называется наклонной асимптотой графика
функции
называется наклонной асимптотой графика
функции
![]() при
при
![]()
![]() ,
если функцию
,
если функцию
![]() можно представить в виде
можно представить в виде
![]() ,
где
,
где
![]() при
при
![]()
![]() .
.
Теорема. Для того чтобы функция
![]() имела при
имела при
![]()
![]() наклонную асимптоту
наклонную асимптоту
![]() ,
необходимо и достаточно, чтобы существовали
два предела
,
необходимо и достаточно, чтобы существовали
два предела
![]() и
и
![]() .
.
