6.4.3. Основные соотношения частотного метода синтеза

На основе выражения (6.29) получим расчетные соотношения частотного метода синтеза. Если удается задать определенную частотную характеристику разомкнутой системы , то из (6.29) можно вычислить . Однако этот способ является громоздким и не нашел практического применения, но на его основе разработан удобный метод синтеза по ЛАЧХ. Запишем его расчетное соотношение, для чего частотную характеристику разомкнутой системы представим в форме

В соответствии с (6.29) для амплитудных частотных характеристик справедливо равенство

которое в логарифмическом масштабе принимает вид

(6.33)

Приравняв правую часть (6.33) , получим

Отсюда следует расчетное соотношение для логарифмической характеристики регулятора, которое является основным в частотном методе синтеза

(6.34)

Таким образом, для расчета регулятора необходимо построить логарифмическую амплитудную частотную характеристику (ЛАЧХ) объекта и на основе требований к качеству процессов в замкнутой системе сформировать ЛАЧХ разомкнутой системы. Затем следует определить ЛАЧХ регулятора в соответствии с выражением (6.34).

6.4.4. Построение асимптотической лачх объекта

Часто модель объекта управления представляет собой последовательную цепочку типовых звеньев, поэтому можно получить, суммируя отдельные ЛАЧХ. Подобное суммирование позволяет предложить следующую процедуру построения .

• На частоте 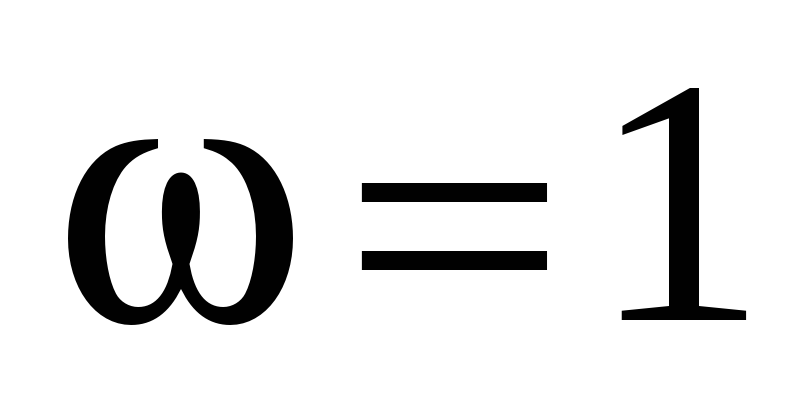(или в логарифмическом масштабе ) фиксируется точка, соответствующая значению, где – коэффициент усиления объекта.

• На оси абсцисс отмечаются частоты сопряжения (или ), , где n – число типовых звеньев в составе передаточной функции объекта.

• До первой частоты сопряжения строится низкочастотная асимптота с наклоном дБ/дек., если содержит интегрирующие звенья, а r – число таких звеньев. Наклон характеристики будет равен дБ/дек., если передаточная функция объекта содержит дифференцирующие звенья, l – число этих звеньев. Низкочастотная асимптота строится таким образом, чтобы она сама или ее продолжение проходили через точку .

• На частотах сопряжения происходит «излом» асимптотической ЛАЧХ объекта. Наклон ЛАЧХ изменяется на дБ/дек., если соответствующая частоте сопряжения постоянная времени находится в знаменателе передаточной функции объекта, r – число таких звеньев. «Излом» асимптотической ЛАЧХ будет равен дБ/дек., если постоянная времени находится в числителе передаточной функции, l – число звеньев. Новая асимптота проводится до следующей частоты сопряжения, где также происходит ее «излом» в соответствии с указанным правилом.

Пример 6.5

Построить асимптотическую ЛАЧХ объекта, передаточная функция которого имеет вид

где коэффициент усиления , а постоянные времени , .

Используем предложенную процедуру для построения ЛАЧХ объекта. Предварительно определим характерные точки:

,

отметим их на осях координат (рис. 6.9).

П

Риc. 6.9. Асимптотическая ЛАЧХ объекта для примера 6.5

остроение ЛАЧХ начинается из области низких частот, которая располо- жена левее первой частоты сопряжения. Низкочастот- ная асимптота имеет наклон – 20 дБ/дек., так как передаточная функция объекта содержит интегрирующее звено. Проводится она до частоты так, чтобы ее продолжение пересекало ось ординат в точке . На частоте происходит «излом» характеристики на –20 дБ/дек., что соответствует апериодическому звену в составе . До следующей частоты сопряжения () асимптота имеет наклон – 40 дБ/дек. «Излом» характеристики на частоте равен – 20 дБ/дек., так как в составе есть апериодическое звено с постоянной времени . Следовательно, наклон последней асимптоты ЛАЧХ объекта будет равен – 60 дБ/дек.

Для построения ЛАЧХ объекта с произвольной передаточной функцией

.

следует перейти к выражению для частотной характеристики

.

Амплитудно-частотная характеристика определяется так:

,

что позволяет вычислить

. (6.35)

Таким образом, логарифмическая амплитудная частотная характеристика объекта находится как разность (6.35).